在我們日常生活中，數位通常都很「實用」，用於計數或測量，範圍也相對容易理解。然而，在數學、電腦科學、天文學等領域裏，有時會遇到那些超乎常人想象的「大數」。這些數如此之大，以至於僅用常規的數學符號和語言都難以表達。例如，你可能聽說過「哥德爾數」、「格雷厄姆數」或是「忙碌河狸數」，這些都是巨大到幾乎無法想象的數位。它們不僅僅是抽象概念，實際上，這些「大數」在理論電腦科學、邏輯學，甚至哲學問題如無限性和可計算性等方面都有著重要的套用和深遠的意義。
這其中有一部份非常引人註目，那就是忙碌河狸數（Busy Beaver）和TREE之間的比較，
Tree 數（TREE(n)）是一個用於描述特定型別的樹結構「大小」的數學序列。該序列在數學邏輯和 Ramsey 理論中有重要套用。盡管 TREE（1）和TREE（2）是相對較小的數，TREE（3）已經大到無法用常規數學表示法描述，遠超過諸如格雷厄姆數這樣的已知大數。這些數因其難以想象的「大小」和數學復雜性而受到廣泛關註。
當你深入研究忙碌河狸數時，會發現這可能是存在的最令人震驚的函式。 實際上，理論上沒有任何演算法能夠生成與這一函式匹配的數位。
如果有某種神奇的暴力計算方法能計算出忙碌河狸函式的一些小的輸入值，那將涉及解決數學中幾個世紀以來未解決的問題。有些數學體系在達到某個點後甚至無法證明其值。這個數，實際上就是一串固定的數位，很明確地劃分了可計算和（Computable）不可計算（Not Computable）的界限。
我對這還不是很了解。這裏主要參照Scott Aronson和其他幾位數學家的工作，
首先，我們需要了解 二進制圖靈機 （Binary Turing Machine）。這是一種抽象裝置，作用於一個由1和0構成的無限長的紙帶上。
這台機器有一個內部狀態，它讀取一個單元，然後根據其狀態和所讀內容寫入1或0，然後向左或右移動，並轉換到一個新狀態。也可能停止計算。
為了表示機器的所有行為，我們使用一個狀態表。這是一個四態機器，因為它有四個不同的狀態（不包括停止狀態）。對於狀態和讀取值的每一種組合，都有三種動作：寫入的值，如何移動，以及轉換到什麽狀態。
例如，如果機器處於狀態A並讀取一個值為0的數據，那麽我們會在上圖紅色框中（1、L、D）尋找以確定接下來的動作。在這種情況下，我們會寫入一個值為1的數據，向左移動，並將狀態切換到D。
然後，我們需要了解兩件關於圖靈機的事情。首先，Church-Turing論文指出， 任何計算（即套用於某些輸入以產生某些輸出的任何有限步驟序列）都等價於某個圖靈機的操作 。這意味著，我們可以把所有的計算，所有的演算法都看作是圖靈機，無論是Python函式，C++程式，還是你的電腦正在執行的任何事情。
其次，圖靈證明了 不存在一種演算法，能接受任何狀態表和任何輸入紙帶作為輸入，並判定機器是否會在該紙帶上停止。這樣的問題是不可判定的。
沒有通用的方式可以簡單地預判一個計算是否會終止，有時必須執行它並等待，而且可能會永遠地等下去，永遠都不知道答案。值得強調的是， 沒有一個單一的演算法能適用於所有機器和紙帶。 在某些特定的機器和紙帶情況下，或許有專門的演算法能決定它是否會停止。
那麽，什麽是 忙碌河狸函式呢（The busy beaver function） ？我們將其記作
實作這個最大值的機器被稱為忙碌河狸機器。
舉個例子，假設n等於2，考慮一個有兩個狀態的表。
透過某個特定的圖靈機，最終紙帶上可能寫下兩個1。
但事實證明，如果用另一台圖靈機，會得到四個1，
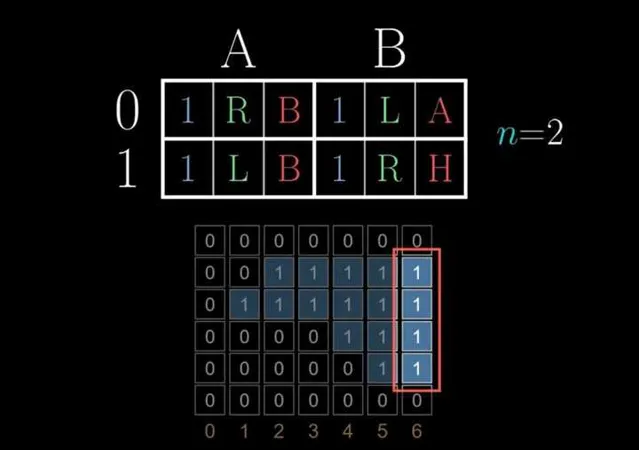
這是最多的，所以Σ（2）是4。
這個過程是如何繼續的呢？對於三狀態的圖靈機，最終紙帶上最多有六個1，所以Σ（3）是6；對於四狀態的圖靈機，最多有13個1，所以Σ（4）是13。 至於五狀態的圖靈機，人類至今還無法計算這個數。
為什麽這麽難計算呢？我們來看看有多少種n狀態的圖靈機，
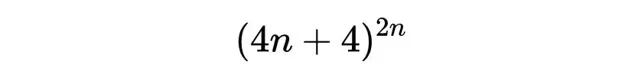
數量是這麽多。可以看到，隨著所考慮的狀態數量的增加，機器的數量是呈指數增長的。當有四個狀態時，那涉及到超過250億台圖靈機，而人類確定了它們能寫入的1的最大數量是13，這已經是一項非常艱巨的工作。
問題在於判定哪些機器會停止，沒有通用的演算法。
因此，我們需要對單個機器進行多年的理論推斷，找出最終會停止的一小部份機器，並執行它們以得出寫入1的最大次數。對於五狀態的圖靈機，這涉及到數萬億台更為復雜的機器。
這個函式有多難呢？首先， Σ(n)甚至不是一個可計算的函式 。一個可計算的函式是那種可以透過有限步驟從輸入產生輸出的函式，但這裏沒有這樣的函式，因為有些機器會永遠執行。在整個執行過程中，我們可能會認為其中一台機器可能是「忙碌的河狸」（Busy Beaver）。
「忙碌的河狸」是一個來自計算理論的概念，用於描述一個特殊型別的圖靈機，這種圖靈機在給定狀態數的限制下，能夠在最終停機（halt）之前打印出盡可能多的「1」。那麽，我們怎麽能計算像Σ（4）這樣的數呢？這裏有一點微妙之處： 不可計算性來自於缺乏一種適用於所有n的有限程式 。但對於特定的n，由於機器數量是有限的，我們可能能夠透過分析找到答案。
有證據表明， 這個序列增長速度超過任何可計算的函式 。 換句話說，在所有可能的函式中，只要輸入一個整數n並在有限時間內返回一個整數，忙碌河狸函式在某個n值之後的增長速度將超過它。
這實在是太不可思議了。簡單地說，任何你能想象到的透過有限步驟處理輸入的方式，都無法超過這一令人驚嘆的數列。
嘗試挑戰王者
讓我們嘗試挑戰忙碌河狸函式。我將構造一個自己的快速增長的函式。首先，我要發明一些符號。假設一個問號代表一個階乘的指數版本。比如4問號，是指4的3次方的2次方的1次方。
從右上角開始向下求值，大約等於262,000，這對於4來說是一個相當大的數位。
現在考慮這個，
得到了一個高達262,000項的指數塔。所以兩個問號後，就得到了一個無用的大數。
接下來，我定義破折號問號，
如果套用到4上，那就是4帶著很多問號，
具體有多少個呢？那將是4問號個問號，
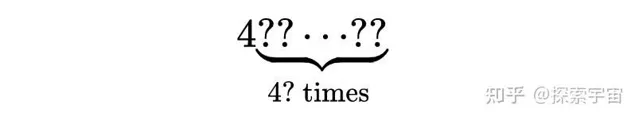
這簡直太瘋狂了。我們再進一步，定義雙破折號問號，
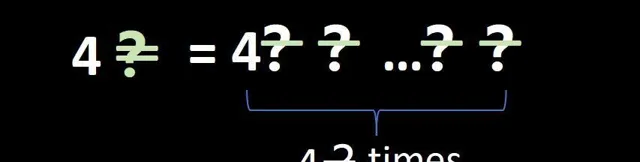
要明確的是，從左邊開始求值，也就是從 4破折號問號 開始，然後把這個數再次代入破折號問號，得到一個超乎想象的數，而且要這樣做很多很多次，實際上要做無數次。
現在，我嘗試用這個去推翻忙碌河狸函式，
效果如何呢？根本不接近！當然，對於小的n，我定義的數是更大的，但一旦超過了某個界限，忙碌河狸函式就會完全碾壓。
但臨界點在哪裏？我們可以用更快增長的 格雷厄姆數g_n（（Graham's number）） 來做一些估計，這是一個比我定義的數增長得更快的數，
格雷厄姆數（Graham's number）是一個非常大的自然數，由數學家隆納·格雷厄姆（Ronald Graham）在解決一個特定的組合最佳化問題時引入。這個數是如此之大，以至於不能用常規的數學符號或科學記數法來表示。
我猜測，在n大概為10的時候，Σ（n）可能會超過我定義的數，僅僅是猜測，如果實際上是8，我也不會感到驚訝。重點是，幾乎是一開始，忙碌河狸數就已經打敗了我的定義的數了。
我們知道忙碌河狸數超過了我定義的數，因為我定義的數是可計算的 ，即透過有限步驟從輸入得到輸出。
事情變得越來越怪異和抽象。 事實上，存在一個27狀態的圖靈機，只有當著名的「哥德巴哈猜想」是錯誤的時才會停止。 這個猜想是數學中最古老、最著名的未解問題之一，它指出大於2的每一個偶數都是兩個質數的和，但至今無人證明。
這意味著，如果直接計算Σ（27），涉及到判斷哪些機器會停止，那就相當於解決了哥德巴哈猜想。 因為我們需要確定哥德巴哈圖靈機是否停止：如果停止，猜想就是錯誤的；否則就是正確的。黎曼猜想也是同樣的道理。
準確地說，也許有一些計算忙碌河狸數但不實際解決這些開放問題的奇怪途徑，但這不是重點。重點是這些數包含了大量的數學資訊，實際上情況還會變得更加復雜。
其數值在某些體系中無法被證明
更奇怪的是，事實證明有些真實的命題，比如說Σ（1000）等於某個數K，
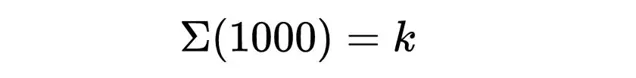
在我們常用的數學公理體系中無法被證明。 也就是說，到了某一點，數學失去了對這些數位作出聲明的能力。
