中介效应的本质——从Baron 和 Kenny (1986)的逐步法讲起
中介分析的目的是检验科学家假想的机制是否正确。所谓机制就是一种系列的影响方式。科学家发现一个现象X会影响Y (X -> Y),为了解释这个现象科学家提出一个假设:X导致M,然后M导致Y(X -> M -> Y)
举例:中世纪某船长发现出海后,船员容易得败血症。用回归方程来描述:
得败血症船员的比例 = c * 是否出海 + b1 + e1 (方程1)
其中(未出海:是否出海 = 0;出海:是否出海 = 1)
船长想要探究为什么出海后得败血症船员的比例上升,即方程1中c>0(p<0.05)。船长假设出海后没有新鲜蔬果导致的维生素C缺乏是船员得败血症的原因。即船长认为维生素C下降是中介变量。为了验证他的假说,他必须证明如下3件事:
(1)出海会导致维生素C缺乏,用回归方程描述:
船员维生素C含量 = a * 是否出海 + b2 + e2 (方程2)
其中a是负数且p<0.05
(2)在控制是否出海后,维生素C缺乏会导致得败血症船员的比例上升。用回归方程描述:
得败血症船员的比例 = c’ * 是否出海 + b * 船员维生素C含量 + b3 + e3 (方程3)
其中a是负数且p<0.05
这里有一个理解上的难点,为什么要控制「是否出海」?这件事可以反过来思考,如果不控制的话会发生什么?假设方程1和方程2中的c和a都显著,即使船员维生素C含量下降与得败血症船员比例之间显著相关,也不能说明维生素C含量低是船员得败血症的原因。因为可能存在下面这种情况,即出海导致船员维生素C和维生素D含量都下降,而维生素D含量下降才是导致败血症的病因,此时维生素C含量与败血症之间是虚假的相关关系。给船员补充维生素C并不能治败血症。
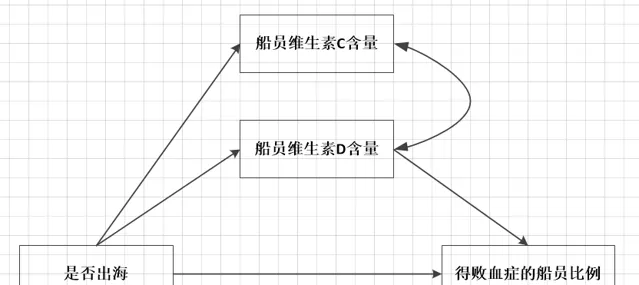
而如果控制「是否出海」,维生素C缺乏仍会导致得败血症船员的比例上升,即方程3中b显著。就说明无论船员是否出海,只要缺乏维生素C,就会得败血症。
(3)方程3中的c‘应该为0或不显著。这就说明维生素C缺乏是出海时海员得败血症的唯一原因。在心理学中,往往很少有这样的唯一原因(完全中介),因此该条件可放宽为c’ < c
上面就是最经典的中介分析。
参考文献:
Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51, 1173–1182.
私人个性化数据分析等服务请联系微信详议
微信号:sgzwrycx










