(本回答的目标读者是线性代数的初学者。)
先回答题主的问题:
矩阵是对线性变换的表示;对于同一个线性变换,基选择的不同,表示该线性变换的矩阵就不同。
接下来我试着解释这句话。
由于我们研究的对象是『 线性变换 』,而不是『矩阵』,所以在继续往下看之前, 建议暂时忘记一切关于『矩阵』的内容 ,直到我提到这个概念为止。
好,开始了呦。
一个线性变换是一个 函数 。一旦确定了函数对于定义域中每一个元素的作用,也就确定了这个函数。对于线性变换来说,我们需要知道 每一个向量 被变换到了哪里。
由于这个变换是 线性 的,所以我们只需要知道 一组基向量 被变换到了哪里,就可以知道任何一个向量的被变换到哪里了。
什么意思呢?我们具体一点来看:考虑一个线性变换T:V\rightarrow W ,我们想要知道V 中每一个向量v 去了哪里,我们只需要知道V 的一组基向量v_{1},...,v_{n} 去了哪里(因为V 中任意向量都是基向量的线性组合),也就是要知道T(v_{k}) 是W 中的哪一个向量。
那我们怎么描述W 中的一个向量呢?同样的道理,我们可以用W 的一组基向量w_{1},...,w_{m} 来描述W 中的任意一个向量。
这下就好办了,为了表示一个线性变换T:V\rightarrow W ,我们选择V 的一组基向量v_{1},...,v_{n} ,再选择W 的一组基向量w_{1},...,w_{m} ,接着,把T(v_{k}) 用w_{k} 表示出来,就搞定了!
也就是说,我们把每一个T(v_{k}) 写成w_{k} 的线性组合:
T({v_{k}})=a_{1,k}w_{1}+...+a_{m,k}w_{m}
再说一遍, 这个式子描述了V 的第k 个基向量被变换到W 中之后的位置。
所以,选定了V 与W 的基向量之后,线性变换可以由a_{j,k} 唯一确定,其中j=1,...,m ,对应的是W 的基,k=1,...,n ,对应的是V 的基。
好了,你肯定猜我要说:『我们把a_{j,k} 写成m\times n 的矩阵中第j 行第k 列的元素。』
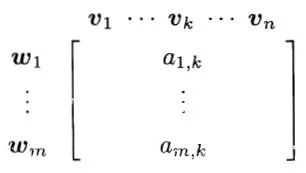
先不急,这句话是对的,但我要说的不是这个。来看一张图:
(这张图的来源是【Linear Algebra Done Right】。)
这张图描述的是我们如何通过选定的V 与W 的基向量来构造m\times n 的矩阵:
把定义域的基向量v_{1},...,v_{n} 写在上方,把目标空间的基向量w_{1},...,w_{m} 写在左侧。
接着,按照之前所说的:
把每一个T(v_{k})
写成基向量w_{i}
的线性组合,所需要的系数就构成了矩阵的第k
列。
把每一个T(v_{k})
写成基向量
w_{i}
的线性组合,所需要的系数就构成了矩阵的第k
列。
把每一个T(v_{k})
写成基向量
w_{i}
的线性组合,所需要的系数就构成了矩阵的第k
列。
最重要的话重复三遍。
再看一下图,从矩阵M(T) 中我们又可以得到T(v_{k}) :将矩阵的第k 列的每个元素与左侧相应的w_{j} 相乘,然后把所得向量相加,就得到了T(v_{k}) 。
以上这部分内容请反复看。
好的,给个例子。偷懒的我就用书上的例子了。
线性变换T:\mathbb{R}^{2} \rightarrow \mathbb{R}^{3} 定义为:
T(x,y)=(x+3y,2x+5y,7x+9y)
我们选择标准基来描述——\mathbb{R}^{2} 的标准基是(1,0),(0,1) ,\mathbb{R}^{3} 的标准基是(1,0,0),(0,1,0),(0,0,1) :
我们想知道T 把\mathbb{R}^{2} 的标准基变换到了哪里,于是代入上式:
T(1,0)=(1,2,7)=1(1,0,0)+2(0,1,0)+7(0,0,1)
T(0,1)=(3,5,9)=3(1,0,0)+5(0,1,0)+9(0,0,1)
于是,T 关于标准基的矩阵是:
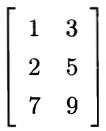
就是这样。嗯。
现在再看『一个矩阵对应了一个线性变换』这个说法,就可以知道这个说法并不严谨。实际上, 只有确定了基向量之后,一个矩阵才对应一个线性变换 ;否则,只要换一组基,同一个矩阵对应的线性变换就不同了。
那为什么我们经常还说『一个矩阵对应了一个线性变换』呢?因为一般来说,如果不明确指出,我们都默认使用标准基。
知道了上述内容,那么矩阵乘法的意义也就很好理解了。
设v_{1},...,v_{n} 是V 的基,w_{1},...,w_{m} 是W 的基,u_{1},...,u_{p} 是U 的基。考虑线性映射S:U\rightarrow V 与T:V\rightarrow W ,分别对应矩阵M(S) 和M(T) 。
当我们定义了矩阵乘法之后,它们的复合映射TS:U\rightarrow W 就对应了M(TS)=M(T)M(S) 。具体的证明在教材上都会有,但我建议最好自己动手验证一下。
但注意,这个优美的性质成立的前提是, 两个矩阵必须选择的是同一组V 的基v_{1},...,v_{n} ,否则不成立。当然,我们一般用的都是标准基,所以大多数时候不会有这个问题。
那如果出现基不一样的情况,该怎么办呢?
答案是:我们可以用矩阵来换基啊!
我们再来看一下之前的图:

矩阵本身的意义中就有『换基』,只是我们一般都用标准基,所以『换基』并没有体现出来。
所以,我个人认为,有些教材上把换基矩阵区分为『无线性变换的换基矩阵』和『有线性变换的换基矩阵』实际上是多余的(但也许这样是为了更直观地描述分解操作),因为 每一个矩阵都是『线性变换+换基』 。
实际上 『无线性变换的换基矩阵』完全可以理解成『恒等变换+换基』 ,所以,空间的维数不变,m=n ,是正方形矩阵。
我们来看一下一些教材上对『无线性变换的换基矩阵』的定义:
如果v_{1},...,v_{n} 和v'_{1},...,v'_{n} 是V 的两组基,对于\forall~ i,j \in \left\{ 1,...,n \right\} ,存在B_{i,j} \in \mathbb{R} ,使得v'_{j}=\sum_{i=1}^{n}{B_{i,j}v_{i}} 。我们把矩阵B=(B_{i,j}) 称为『把v'_{i} 换成v_{i} 的换基矩阵』。
于是有人就不理解了,看v'_{j}=\sum_{i=1}^{n}{B_{i,j}v_{i}} 这个描述,这个矩阵B 明摆着是把v_{i} 变成了v'_{i} 呀,为什么要反过来说呢?
其实并没有反,正如我之前所说的,B 实际上是『恒等变换+换基』的矩阵,跟其他矩阵没有什么不同:I(v'_{j})=\sum_{i=1}^{n}{B_{i,j}v_{i}} ,这样一来,再看一下之前的那张图,v'_{i} 是写在上方的,v_{i} 是写在左侧的。所以, 这个矩阵其实描述一个恒等变换,变换之前用的是一组基v'_{i} ,变换之后用的是另一组基v_{i} ;而由于恒等变换的效果看不出来,所以这个矩阵看起来就只是在换基。
这样一来,『为什么把非标准基换成标准基的矩阵就是把非标准基的向量竖着写下来』也就一目了然了,因为每一个非标准基向量写成标准基的线性组合,系数恰好就是该向量的对应位置的坐标。(把这个想清楚对于理解矩阵很重要。)
而『把v'_{i} 换成v_{i} 的换基矩阵』与『把v_{i} 换成v'_{i} 的换基矩阵』这两个矩阵是 互逆 的,这个很容易证明。( 证明它!! )
于是,对角化矩阵就很好理解了。
一个线性变换T 对于标准基(或者其他某个基)的矩阵为A ;而我们为了更清楚地通过矩阵看出这个线性变换的效果,就把A 对角化:
A=PDP^{-1} (D 为对角矩阵)
这其实就是先把标准基换成由特征向量组成的基(这是P^{-1} 的意义),于是每一个基向量在经过T 变换之后都只是乘了一个常数(这是D 的意义),最后再把由特征向量组成的基换回标准基(这是P 的意义)。
而刚刚说过,『把非标准基换成标准基的矩阵就是把非标准基的向量竖着写下来』,所以(按照D 中特征值的顺序)把对应的特征向量竖着写下来,就得到了P 。
所以对角化其实就是要 用一组比标准基更好的基来描述线性变换 ,也就是 由特征向量组成的基 。
那有没有比这个更好的基呢?有呀,就是 由特征向量组成的规范正交基 ,而这正是 谱定理 所研究的对象,这里就不叙述了=w=
写这个回答是因为我发现,很多时候别人问我问题,都是由于还没有清晰地理解矩阵与线性变换之间的关系,而我觉得这应该是线代的基础中的基础。所以就把这些东西写在这里,希望对题主和其他人有所帮助,同时自己也再巩固一遍。
那么就写到这里。马上去上课了!
这篇回答依然献给那个正在学线代的小朋友=w=
那么就这样=w=











