这篇回答里我主要想讲高阶矩( \geq 3 ),因为一阶矩(期望值)和二阶矩(方差)相对来说并不难理解。而看这个问题的措辞,题主也是对高阶矩比较困惑。
在我看来,高阶矩的目的是去测量一个分布的 重尾程度 ,或者说概率 p(x) 是否 随着值 x 的增大急速地减少。
听起来有点抽象,那让我首先来解释重尾是什么意思。
在研究一个分布的时候,我们很多时候可能会 对极大值特别的敏感 。比如说,我是一个小型公司的老板,收到了一份这样的风险分析,0.1 的概率赔10万,0.05 的概率赔20万,等等。这些数字我大概都是一扫而过,因为这些钱我完全赔的起。但假如说我看到了一个0.01 的概率赔1000万,我估计眼睛就瞪圆了。虽然说0.01不算是一个大的概率,但是赔这么多钱我们公司可能就破产了。
所以说,对于特别大的值,光是概率小是不够的,我们可能需要概率 非常非常小 。由于画图时这些极大值会出现在图像的边界,我们称这些极大值为分布的 尾部 。
比如,下图是我们熟悉的高斯分布。 尾部就是出现在图像的边缘。但是提到尾部,我建议不要想到4,5个 std开外,而是去想象几十个甚至更多std开外。
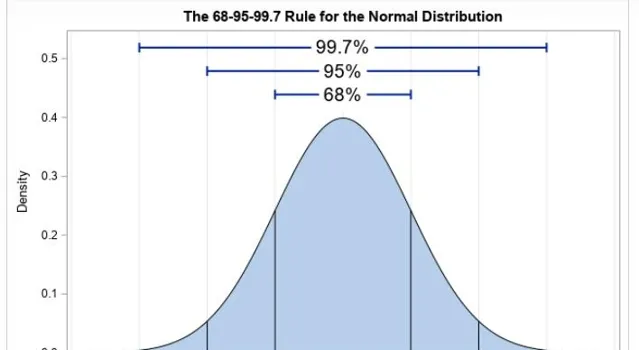
现在我们回头看一下k阶矩的定义。为了方便我只考虑k为偶数,期望值为零的情况。
\mu_k = \int_{-\infty}^{\infty}x^kp(x)dx 。
在这里我们可以将 \mu_k 理解成对于重尾现象的厌恶值,而k可以理解成一种加权。
想象我们会根据一个随机函数x的重尾程度对其扣分。
当k=3的时候,x = 1000 对应着扣10^9分。
当k=4的时候,x = 1000对应着扣10^12分。
。。。。
。。。。
当k=10的时候,x=1000对应着扣10^30分。
我们可以看到,随着k的增大,极大值对高阶矩的影响会 急速 地增大(注意,是急速)。
在这种情况下,如果说希望 \mu_k 不跟着爆炸的话,那么只有一种可能:
p(x)会随着x的增大而急速的减小,从而抵消x^k的疯长。
为了阐述这一点,我觉得可以重新看一下大家比较熟悉的高斯分布 N(0,1) , 这是一个典型的轻尾分布。
下面是一个大家可能不是很熟悉的性质。
对于 N(0,1), 有 P(x>t)\leq e^{-\frac{t^2}{2}} 。
也就是说,随着x的增大,概率会以指数的速度下降!
这个速度非常之快,大家可以很容易算得 p(x>10)\leq e^{-50} = 3.72*10^{-44}.
而上述这个性质也同样可以用高阶矩来表示,即为
对于任意k, \mu_k\leq k^{\frac{k}{2}} 。
而对于那些重尾的分布, \mu_k 可能就没有这种上界了,很多时候如果k比较大\mu_k 直接就是无穷。
所以,有这样一层对应关系
\mu_k 缓慢增长 等同于 分布的概率随着x的增长快速下降。
这对于我来说是一个非常有用的认识,也希望能够对大家有帮助。











