機器學習想解決什麽問題?答案是機器學習的野心很大,希望用機器解決一切人們期望解決的問題,比如文字/語音/影像辨識、與人對話、完成科研任務等等,總之希望機器可以具備甚至超越人類智慧。
雖然現階段機器學習還不具備超越人類的智慧,但隨著 ChatGPT 的釋出,大家都看到,機器已基本具備人類智慧,甚至在某些領域已部份超越了人類智慧。可能在幾年前,人們還在質疑當前機器學習方向是否正確,但隨著近期取得的巨大突破,人們的信念變得堅定,越來越多的頂級聰明人投入了這個方向。
所以在這個時代,任何人最好都了解一些機器學習的原理,就算被機器超越,也要知道個明白。
機器學習就是找函數
以我對機器學習的理解,認為其本質就是 找函數 。我需要從兩個角度解釋,為什麽機器學習就是找函數。
第一個角度,為什麽要找函數 。因為人解決問題與機器解決問題本質的不同,人能解決問題,但不一定能說清楚背後的原因,而機器解決問題靠的是計算,是可以重復執行且邏輯精確的。所以用機器解決人類解決的問題,也必須找到精確的函數,即便這個函數會非常復雜。
第二個角度,為什麽相信能找到函數 。我們憑什麽認為人類智慧才能完成的任務,可以找到函數解?現實就是 ChatGPT 找到了,所以說明可以找到函數解!也許因為 ChatGPT 背後的神經網絡是高維函數,高維函數投影到我們低維的時空能解決所有問題,說明我們被降維打擊了。
以上只是一些隨口說的感慨,接下來我們進入幹貨階段。
假設世間所有問題都抽象為輸入、輸出
既然我們相信能找到解決一切問題的函數,那這個問題也必須能描述為輸入,輸出的模式 。比如:
就像知乎的 slogan "有問題就會有答案",世界上絕大部份需要人類解決的問題,似乎都能透過輸入、輸出解決。
好,當我們覺得世間所有問題都能抽象為輸入輸出,那如果我們找到了一個函數,對於每一種輸入,結果輸出都是人類認可的正確答案,那這個函數不就是一個超級智慧大腦嗎?
假設我們發現了一個函數 f(x):
f("小紅有3個蘋果,給了小明1個,還剩幾個?") = "2個"
f("我真是謝謝你們的服務,烤冷面外賣送到的時候真成了冷面。這句話是正面還是負面評價?") = "負面"
那就認為,對這兩個例子來說,函數 f(x) 就是機器學習要找的函數。
那麽難點來了,怎麽找到這個函數呢?
如何找到這個完美函數
ChatGPT 幾乎已經找到了這個完美函數,它可以幾乎解決一切問題,這也是我們學習機器學習的動力。但作為初學者,只盯著火箭是永遠也學不會的,讓我們先從擰螺絲開始。
我們降低一下目標,把要找的函數設定為 y = 3x,即我們要找一個函數 f(x),
f(1) = 3
,
f(2) = 6
,
f(10) = 30
。
有人會說這不簡單嗎,y = 3x。嗯,別急,我們此時還不知道答案呢,或者當問題變得非常復雜時, 靠人腦根本找不到函數的運算式時,怎麽樣才能讓函數尋找得以繼續?
我們必須找到一條通用的路線,讓無論這個函數的運算式是什麽,都可以透過輸入與輸出自動尋找,讓電腦幫我們自動尋找,哪怕付出非常大的計算代價,這就是機器學習領域說的 「訓練模型」(training)。
換句話說,我們設定的方法必須能拓展到任意的輸入輸出,這樣我們才可能訓練
f("小紅有3個蘋果,給了小明1個,還剩幾個?") = "2個"
這樣的模型,也就是說,這個方法必須僅憑輸入輸出就可以運作,而不需要依賴任何人類數學知識的幹預,這樣才可執行。
機器學習最重要的三部曲出現了,它用在尋找 y = 3x 這種函數上看著很蠢,但用在更復雜的函數上,卻如神來之筆。
找函數三部曲
機器學習理論最早由 沃倫·麥卡洛克、禾特·皮茨 提出,後續大部份貢獻都由英國、美國、德國、法國、加拿大等國人推動,所以絕大部份是英文資料,所以我們耳熟能詳的關鍵詞都是英文詞匯,轉譯成中文反而表述或者含義上容易引發歧義,所以為了效率,關鍵詞匯還是寫成英文好了。
還是以尋找 y = 3x 為例,假設我們不知道要找的函數 f(x) = 3x,但知道一些零星的輸入輸出,比如
f(1) = 3
,
f(2) = 6
,
f(10) = 30
,這些輸入輸出組合成為 Training data(訓練資料)。Training data 是比較好找的,好比想要訓練一個判斷一個句子是積極還是消極的場景,要直接寫出 f(x) 是極其困難的,但舉一些正向或者負向的例子確實很容易的,比如:
f("商品很好用") = "積極"
f("杯子都碎了") = "消極"
f("下次還買") = "積極"
這些輸入與輸出的組合就是 Training data,找函數三部曲就是僅憑 Training data 就能找到它的實作函數,這就是機器學習的美妙之處。
第一步 define model function
define model function 就是定義函數,這可不是一步到位定義函數,而是定義一個具有任意數量未知參數的函數骨架,我們希望透過調整參數的值來逼近最終正確函數。
假設我們定義一個簡單的一元一次函數:
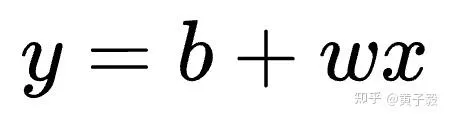
其中未知參數是 w 和 b,也就是我們假設最終要找的函數可以表示為 b + wx,但具體 w 和 b 的值是多少,是需要尋找的。我們可以這麽定義:
const
modelFunction
=
(
b
:
number
,
w
:
number
)
=>
(
x
:
number
)
=>
{
return
b
+
w
*
x
;
};
其中 w 表示 weights(權重),b 表示 bias(偏移),對這個簡單的例子比較好理解。這樣對於每一組 w 和 b,都能產生一個唯一的函數。
你也許會覺得,一元一次函數根本不可能解決通用問題。對,但為了方便說明機器學習的基本原理,我們把目標也設定為了簡單的 y = 3x。第二步 define loss function
define loss function 就是定義損失函數,這個損失可以理解為距離完美目標函數的差距,可以為負數,越小越好。
我們需要定義 loss 函數來衡量當前 w 與 b 的 loss,這樣就可以判斷當前參數的好壞程度,才能進入第三步的最佳化。因此 loss 函數的入參就是第一步 model function 的全部未知參數:w 與 b。
有很多種方法定義 loss 函數,一種最樸素的方法就是均方誤差:

即計算當前實際值
modelFunction(b,w)(x)
與目標值
3x
的平變異數。那麽 loss 函數可以這樣定義:
const
lossFunction
=
(
b
:
number
,
w
:
number
)
=>
// x 為 training data 輸入
// y 為 training data 對應輸出
(
x
:
number
,
y
:
number
)
=>
{
// y',即根據當前參數計算出來的 y 值,函數名用 cy 表示
const
cy
=
modelFunction
(
b
,
w
)(
x
);
return
Math
.
pow
(
y
-
cy
,
2
);
};
上述函數在給定 w 與 b 的下,計算在某個 training data 下的 loss,在呼叫處遍歷所有 training data,把所有 loss 加起來,就是所有 training data 的 loss 總和。
為了讓尋找的函數更準確,我們需要想辦法讓 loss 函數的值最小。
第三步 optimization
optimization 就是最佳化函數的參數,使 loss 函數值最小。
我們再重新梳理一下這三步。第一步定義 model function,包含了 n 個未知參數,第二步定義 loss function,選擇比如均方誤差的模型,值的計算依賴於 model function,第三步希望找到這 n 個參數的值,使得 loss function 值最小。
因為 loss function 定義就是值越小越貼近要尋找的目標函數,所以最小化 loss function 的過程就是尋找最優解的過程。
而尋找 loss function 的最小值,需要不斷更新未知參數,如果把 loss 函數畫成一個函數影像,我們想讓函數影像向較低的值走,就需要對當前值求偏導,判斷參數更新方向:
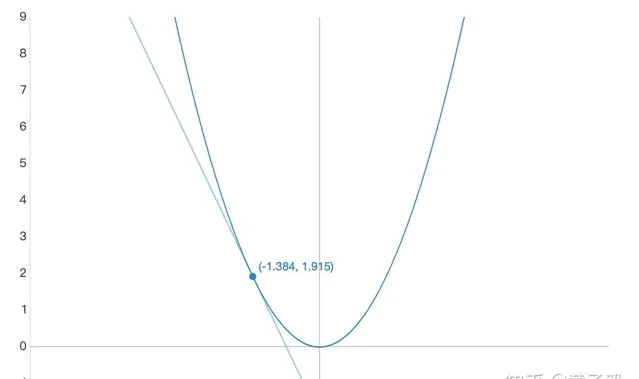
如上圖所示,假設上圖的 x 軸是參數 w,y 軸是此時所有 training data 得到的 loss 值,那麽只要對 loss 函數做 w 的偏導,就能知道 w 要怎麽改變,可以讓 loss 變得更小(當偏導數為負數時,右移,即 w 增大可以使 loss 減小,反之亦然)。
根據 loss function 的定義,我們可以分別寫出 loss function 對參數 b 與 w 的偏導公式:
對 b 偏導:

對 w 偏導:
 註意,這裏僅計算針對某一個 training data 的偏導數,而不用把所有 training data 的偏導數結果加總,因為後續如何利用這些偏導數還有不同的策略。
註意,這裏僅計算針對某一個 training data 的偏導數,而不用把所有 training data 的偏導數結果加總,因為後續如何利用這些偏導數還有不同的策略。
那麽程式碼如下:
const
optimization
=
(
b
:
number
,
w
:
number
)
=>
(
x
:
number
,
y
:
number
)
=>
{
const
gradB
=
-
2
*
(
y
-
modelFunction
(
b
,
w
)(
x
));
const
gradW
=
-
2
*
x
*
(
y
-
modelFunction
(
b
,
w
)(
x
));
return
{
gradB
,
gradW
};
};
接著我們就可以使用 training data 開始訓練,不斷更新參數 w 與 b 的值,直到 loss function 的值下降到極限,就可以認為訓練完畢啦。
訓練有三種方式使用偏導數,隨機梯度下降、批次梯度下降與小批次梯度下降。它們的區別僅在於什麽時候真正更新 w 與 b。
程式碼實踐
假設我們采用批次梯度下降,training 的過程如下:
細心的你可能發現在 training 過程中,用到了 optimization 與 model function,但沒有直接用到 loss function。其實 optimization 的定義取決於 loss function 的形態,因為 optimization 更新參數的邏輯就是對 loss function 求偏導,所以雖然函數呼叫上沒有直接關系,但邏輯上 model function、loss function、optimization 這三者就像齒輪一樣緊緊咬合。
以如下 training data 為例,看一下較為直觀的訓練過程:
// y = 3x
const
trainingData
=
[
[
1
,
3
],
[
2
,
6
],
[
3
,
9
],
[
4
,
12
],
[
5
,
15
],
];
// 初始化 b 和 w 參數
let
b
=
initB
;
let
w
=
initW
;
// 每次訓練
function
train
()
{
let
gradBCount
=
0
;
let
gradWCount
=
0
;
trainingData
.
forEach
((
trainingItem
)
=>
{
const
{
gradB
,
gradW
}
=
optimization
(
b
,
w
)(
trainingItem
[
0
],
trainingItem
[
1
]
);
gradBCount
+=
gradB
;
gradWCount
+=
gradW
;
});
b
+=
(
-
gradBCount
/
trainingData
.
length
)
*
learningRate
;
w
+=
(
-
gradWCount
/
trainingData
.
length
)
*
learningRate
;
}
// 訓練 500 次
for
(
let
i
=
0
;
i
<
500
;
i
++
)
{
train
()
}
先隨機初始化參數 b 與 w,每次訓練時,計算參數 b 與 w 在每個訓練數據的偏導數,最後按照其平均值更新,更新方向是導數的負數方向,所以 gradCount 前面會加上負號,這樣 loss 才能往低處走。learningRate 是學習速率,需要用一些 magic 的方式尋找,否則學習速率太大或者太小都 train 不起來。
把函數尋找過程視覺化,就形成了下圖:

可以發現,無論初始值參數 b 和 w 怎麽選取,最終 loss 收斂時,b 都會趨近於 0,而 w 趨近於 3,即無限接近 y=3x 這個函數。
至此,我們擁有了一個很簡單,也很強的機器學習程式,你給它任意 x、y 點作為輸入,它就可以找到最為逼近的線性函數解。
總結
作為機器學習的第一課,我們學習了利用 define model function - define loss function - optimization 三部曲尋找任意函數,其中反映出來的是不依賴人類經驗,完全依靠輸入與輸出,讓機器探索函數形態的理念。
雖然我們舉的 y=3x 例子比較簡單,但它可以讓我們直觀的了解到機器學習是怎麽找函數的,我們要能多想一步,設想當函數未知參數達到幾十,幾百,甚至幾千億個時,靠人類解決不了的問題,這個機器學習三部曲可以解決。
也許你已經發現,我們設定的 y = b + wx 的函數架構太過於簡單,它只能解決線性問題,我們只要稍稍修改 training data 讓它變成非線性結構,就會發現 loss 小到某一個值後,就再也無法減少了。透過圖可以很明顯的發現,不是我們的 define loss function 或者 optimization 過程有問題,而是 define model function 定義的函數架構根本就不可能完美匹配 training data:
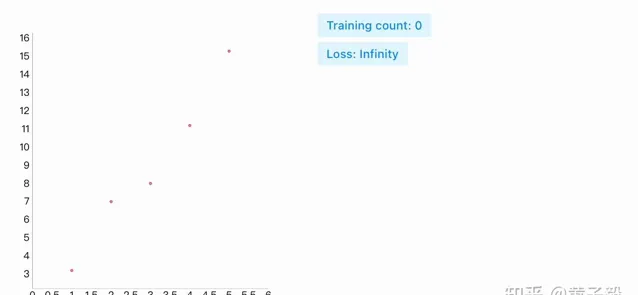
這種情況稱為 model bias,此時我們必須升級 model function 的復雜度,升級復雜度後的函數卻很難 train 起來,由此引發了一系列解決問題 - 發現新問題 - 再解決新問題的過程,這也是機器學習的發展史,非常精彩,而且讀到這裏如果你對接下來的挑戰以及怎麽解決這些挑戰非常感興趣,你就具備了入門機器學習的基本好奇心,我們下一篇就來介紹,如何定義一個理論上能逼近一切實作的函數。











