這個問題挺好的,因為在我們身邊「絕大多數人認為程式設計師非常擅長修電腦」的環境下,編程和數學到底有哪些聯系,或者說數學給了哪些支撐?相信你讀完本文就會有一個大致的輪廓了。
有句話這麽講的,「電腦是數學家一次思考失敗的產物」。
為什麽這麽說?如果去翻一下電腦的發展史,在第一台電腦ENIAC誕生之前,電腦的先驅,圖靈,他是一位數學家...
我們先簡單來捋一下編程的發展,這裏我們先暫不討論我們經常說的演算法,程式內在的邏輯必然是由演算法支撐的,這一點毫無疑問,而演算法的內在就是數學。
圖靈提出了圖靈機模型,可以視為抽象意義上的」電腦「(一種概念)。
什麽是圖靈機呢?
圖靈機:
圖靈機(Turing machine)是一種理論上的抽象計算模型,由英國數學家和邏輯學家阿蘭·圖靈(Alan Turing)於1936年提出。它被認為是電腦科學的基礎,用於理解計算的本質和計算問題的可解性。
圖靈機包含以下幾個要素:
無限長的紙帶(Tape) :圖靈機使用一條無限長的紙帶,紙帶上劃分成一個一個的格子,每個格子上可以寫上一個符號,這些符號可以是有限的字元集。
讀寫頭(Head) :圖靈機擁有一個讀寫頭,它能夠在紙帶上左右移動,並且可以讀取當前所在格子上的符號,也可以寫入新的符號。
狀態集合(States) :圖靈機具有一系列狀態,每個狀態對應著不同的操作。圖靈機根據當前狀態和讀取頭所在格子的符號來決定下一步要執行的操作,然後切換到新的狀態。
轉移規則(Transition Rules) :圖靈機的行為由一組轉移規則定義,每個轉移規則指定了在特定狀態下讀取頭所在格子的符號以及當前狀態的情況下,應該執行什麽操作(如寫入新符號、移動讀寫頭、切換狀態)。
圖靈機的工作方式是,它從初始狀態開始,根據當前狀態和讀取頭所在格子的符號,尋找相應的轉移規則,執行規則所定義的操作,然後切換到新的狀態。這個過程一直持續下去,直到圖靈機進入一個特定的終止狀態,或者執行無限多次操作。
它被證明能夠模擬任何其他形式的計算,因此它被認為是通用計算模型。 模擬的這種計算,就是我們日常生活中的編程。
圖靈是一位邏輯學家,數學家,當一門學科的創始人是數學家的話,那麽我們是不是可以認為這門學科的基礎就是數學?這一門學科就是電腦科學。

接下來我會繼續討論電腦科學中的一些人物,他們在整個電腦發展史起到了重要的作用,而他們無一例外都在數學上有很高的造詣,直到後來電腦科學慢慢成熟起來,我們才開始用電腦科學家來稱呼他們。
約翰·麥卡錫
不是那個」麥卡錫主義「的麥卡錫。
麥卡錫發明了Lisp語言,這門程式語言不同於其他程式語言,他是屬於一個新的編程範式,不同於我們常用的指令式編程。
我們把它稱為函數語言程式設計,或者泛函編程。
函數語言程式設計或稱函數程式設計、泛函編程,是一種編程範式,它將電腦運算視為函數運算,並且避免使用程式狀態以及易變物件。其中,λ演算為該語言最重要的基礎。而且,λ演算的函數可以接受函數當作輸入和輸出。—以上來自wiki
而前面提到的λ演算的提出者也是一位著名的數學家-丘奇。
對函數語言程式設計感興趣的可以參考:

在大學專業課程中,我們會接觸到一門學科:布爾代數。
這門學科給我們在程式中編寫各種分支,判斷,迴圈結構提供了數學上的支撐。
簡單來說,if(condition)中的condition,就是以它為基礎 (如&&,||,!)
基本理論在布爾代數上的運算被稱為AND(與)、OR(或)和NOT(非)。代數結構要是布爾代數,這些運算的行為就必須和兩元素的布爾代數一樣(這兩個元素是TRUE(真)和FALSE(假))。亦稱邏輯代數.布爾(Boole,G.)為研究思維規律(邏輯學)於1847年提出的數學工具.布爾代數是指代數系統B=〈B,+,·,′〉
它包含集合B連同在其上定義的兩個二元運算+,·和一個一元運算′,布爾代數具有下列性質:對B中任意元素a,b,c,有:
1.a+b=b+a, a·b=b·a.
2.a·(b+c)=a·b+a·c,
a+(b·c)=(a+b)·(a+c).
3.a+0=a, a·1=a.
4.a+a′=1, a·a′=0.
隨著電腦、通訊的發展,資訊的安全可靠越來越重要。
密碼學,是一門很古老的學科,古代就被運用於校驗身份等(大將軍調兵,虎符)
我們這裏簡單說一下一個很重要的加密演算法,他也是HTTPS協定的一個底層基礎演算法。
RSA加密演算法,它是1977年由朗奴·李維斯特(Ron Rivest)、阿迪·薩莫爾(Adi Shamir)和李安納·阿德曼(Leonard Adleman)共同提出的一種加密演算法,RSA就是他們三人姓氏開頭字母拼在一起組成。

RSA加密演算法的原理是基於數論中的兩個重要問題:質因數分解問題和離散對數問題。
具體來說,RSA演算法的加密過程如下:選擇兩個大質數p和q,計算N=p*q。
計算φ(N)=(p-1)*(q-1)。
選擇一個整數e,1<e<φ(N),且e與φ(N)互質。
計算d,使得e*d=1 mod φ(N)。
將N和e作為公鑰,N和d作為私鑰。
加密數據時,將明文轉換為整數M,計算C=M^e mod N。
解密數據時,將密文轉換為整數C,計算M=C^d mod N。
又是一門數學的分支學科。
另外還有圖論等等這些,都支撐著編程。
比如:
單源最短路徑,最小生成樹,網絡流... 想一下高德地圖,如果沒有這些圖演算法,導航還會存在嗎?
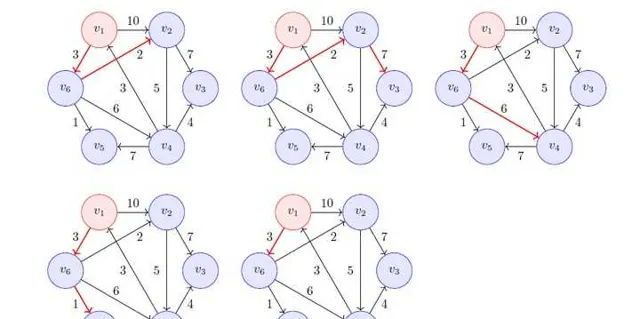
不僅是編程,很多學科在深入挖掘底層根本原理時,可能最終都會回到數學層面。










