對數據做一些變換的 目的是它能夠讓它符合我們所做的假設,使我們能夠在已有理論上對其分析。
對數變換(log transformation)是特殊的一種數據變換方式, 它可以將一類我們理論上未解決的模型問題轉化為已經解決的問題。 我將說兩類比較有代表性的模型。
先給個很經典的例子,如分析美國每月電力生產數。
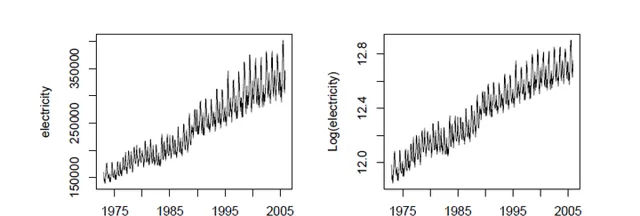
左邊是正常數據,可以看到隨著時間推進,電力生產也變得變異數越來越大,即越來越不穩定。這種情況下常有的分析假設經常就不會滿足(誤差服從獨立同分布的正態分布,時間序列要求平穩)。
這必然導致我們尋求一種方式讓數據盡量滿足假設, 讓變異數恒定,即讓波動相對穩定 。而這種目的可以透過對數轉換做到。
理論上,我們將這類問題抽象成這種模型,即 分布的標準差與其均值線性相依 。
即\sqrt{Var(Z_{t})} =\mu _{t}\times \sigma ,其中E(Z_{t}) =\mu _{t} 。
由定義可推:Z_{t}=\mu _{t}\left( 1+\frac{Z_{t}-\mu _{t}}{\mu _{t}} \right) ,利用log函數的性質:log(1+x)\approx x (當x足夠小)
那麽log(Z_{t})\approx log(\mu _{t})+\frac{Z_{t}-\mu _{t}}{\mu _{t}} .
那麽很容易就知道E(log(Z_{t})) \approx log( \mu _{t}) 和Var(log(Z_{t})) \approx \sigma ^{2} .
所以對數變換能夠很好地將 隨著自變量的增加,因變量的變異數也增大的模型 轉化為我們熟知的問題。
再給個例子:實際研究中,某一研究物件自身性質難以研究,但其增長率是服從一定分布。例如說:Z_{t}=(1+X_{t}) \times Z_{t-1} ,其中X_{t} 是每年增長率(不很大)。
我們可以考慮對數變換:log(Z_{t})-log(Z_{t-1})=log\left( \frac{Z_{t}}{Z_{t-1}} \right)=log\left( 1+X_{t} \right)\approx X_{t}
這樣,我們又可以將 研究數據的增長率分布存在一定規律的模型 轉化為我們熟知的問題。
在對數轉換後,人們又思考了很多其他的轉換方式(如Cox-Box轉換)。但總而言之,每一種轉換方式都是為了讓數據符合我們的假設,來對其進行分析。我所說的對數變換原因只是冰山一角,如有不正確的地方還請各位多多指正。










