照本宣科一番。看回答的同誌們能不能多發幾個評論?提出疑問或者指出錯誤都行,我希望能跟大家多討論討論。這幾天點贊喜歡收藏比我之前的回答都多,結果只有一條評論。。。。
首先聲明:本回答 不是我自己推導 的,僅僅選擇性 轉述了李俊清老師在中國科學技術大學出版的【物質結構導論】第三章中的部份內容 。我也是借此機會復習一下在我看來量子化學中對於有機化學專業學生最具有啟發和理論支撐價值的一部份內容。我個人數學功底不是很好,所以在接觸這些推導過程的時候喜歡聯系一些化學影像來輔助理解。我把這些 自己的體會和思考,以及一些自己犯過的錯誤、有偏差的想法都補充在推導過程旁邊 ,希望可以對跟我一樣不擅長數學的同學有所幫助。 【物質結構導論】 這本書比較老了,可能不太好找。也可以參考Ira N. Levine的【Quantum Chemistry 7th Edition】(Pearson, 2012; ISBN-13: 978-0-321-80345-0)Chapter 13。推導過程是基本一樣的。我個人強烈推薦用這兩本書學習量子化學。前者數學推導基本嚴格但不是太繁瑣,論證簡潔,適合新手上手。後者我打算過年再看一遍重新學習一下。
重申一遍:我數學確實不太好,所以下面的 過程可能不嚴謹,歡迎大家批評指正 。我絕對沒有說數學不重要的意思,而且我覺得良好的數學基礎對於學好量子化學是很巨大很巨大很巨大的助力。但是如果一些同學和我一樣實在沒有能力自己獨立地推導某些積分或者變形過程,我覺得問題也不是很大。但是,我們必須要意識到我們做一切數學工作的目標是什麽。只要緊扣解決問題的策略,我們就可以理解大部份數學變化的動機,以及某些近似成立的原則和帶來的問題。這些理解是很重要的。如果你不用應付考試,你甚至可以不記住某些公式的具體形式;但是我們應該做到看到某個公式就能明白它所描述的物理影像。
本回答旨在透過簡化的線性變分法解p+氫分子離子的薛定諤方程式來解釋分子軌域中成鍵反鍵的由來。我們應該首先認識到:所謂成鍵和反鍵只是結果,是電子填充到能量不同的軌域上造成的分子結構變化。它的產生原因比較難以用經典力學解釋,或者用宏觀世界的模型來類比。
先厘清一些基本觀念:在量子化學的框架下,任何一個原子核和電子構成的體系(比如原子、分子)都可以用一個薛定諤方程式來描述;它們的形式會隨著構成元素的不同而變化(比如核的數量、核電荷數、電子數量等)。薛定諤方程式是一個偏微分方程式,它的解是一個(組)函數( Ψ1,Ψ2,Ψ3.... ),這些函數被稱為波函數。通常,當體系較為復雜時薛定諤方程式沒有嚴格解析解;比如氫氣,這就已經很復雜了,我們一般不會去求氫氣分子薛定諤方程式的解析解。但是,我們有很多方法用近似手段來簡化求解過程,而且實驗證明這些近似方法的結果是很精確的。
一種極其常用的近似思路是:我們可以利用 可嚴格求解的原子軌域 來擬合一個 分子軌域 。這裏所謂「軌域」,其本質某個體系薛定諤方程式的波函數 Ψ 。它的數學基礎是:原子軌域薛定諤方程式的解(波函數)構成一個完備的集合,即它們的線性組合(如式4)能夠構成所有復函數。我們把分子軌域分解成原子軌域線性組合的形式之後,就可以作進一步的簡化,並且套用一些原子軌域的現成結論。所謂的成鍵軌域和反鍵軌域,就是一個給定分子體系薛定諤方程式的 某一組的兩個解 ;它們均滿足薛定諤方程式,但能量本征值不同。
薛定諤方程式和它的解究竟可以怎樣描述分子體系呢?首先,波函數本身沒有明確的物理意義,但對它做算符作用可以求解體系的能量(如式###);而所謂的電子雲,本質是一個概率密度函數,而且它和波函數的關系是:
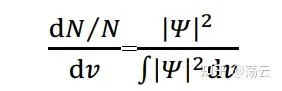
上式左側表示體積微元d v 中出現粒子的數量與總粒子數之比,即「概率密度」。右側分母對於標準化的波函數為1。而右側的分子「絕對值的平方」的展開形式為:
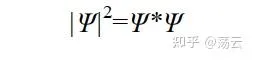
之所以寫成 Ψ* · Ψ (前面的函數加*表示其共軛復函數),是因為波函數 Ψ 是一個含有復變量的函數。
沒學過復變函數的同學不必糾結這些數學,這不是重點。你只需要知道以下兩點:
- 一個分子體系可以由薛定諤方程式描述,它的解是波函數,反映了分子的性質,至少包含以下兩方面的物理意義:(1)波函數的平方是概率密度函數,就是體系電子雲的分步。(2)波函數可以透過算符作用表示體系的能量。
- 由於薛定諤方程式通常難以精確求出解析解,所以我們要做近似和簡化。具體的方法是,首先假定分子薛定諤方程式的解(分子軌域)可以寫成原子軌域線性組合的形式(而且事實上這在數學上是嚴密的)。稍後我們會介紹如何進行這種操作,以及它為什麽可以簡化計算。
好了,上面這些只是提供一點基本認識框架,簡單地介紹了我們的任務和解決問題的基本策略,避免沒有基礎的同學對下方推導中進行某些變換的動機提出疑問。以下開始正式推導。
對於氫分子離子p+,即兩個質子一個電子構成的體系,如圖:
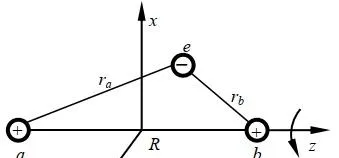
該模型中的成鍵,即電子結構可由電子波函數和能量描述。問題歸結為解這個體系的 Schrödinger 方程式 。 Ψ 為體系波函數。
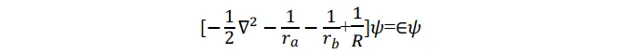
這個方程式在橢球座標系下可以精確求解, 但是多電子分子的 Schrödinger 方程式都不能嚴格求解,所以該方程式的精確求解沒有普遍性。下面用 線性變分法 近似 求解該方程式。
對於在基態下的 p+,如果電子在氫核 a 附近運動,即 ra<<rb,ra<<R,則方程式可近似地寫為
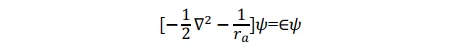
其形式滿足氫原子a的Schrödinger 方程式,其基態即為氫原子1s態。同理,當p+的電子在氫核 b 附近運動時,其基態也是氫原子的 1s 態。所以1sa和1sb兩個原子軌域函數應均滿足上述薛定諤方程式。當電子分別在a核和b核附近運動時,應分別有:(本段的說法我個人感覺不太完善,歡迎大佬補充更好的解釋)
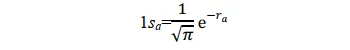
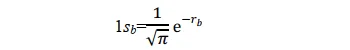
當p+的電子在其它區間運動時,其基態應不同於 1sa 或 1sb;但應與 1sa 或 1sb 有關,因為至少在電子分別靠近兩個核時的特殊情況下, Ψ 可以別近似為 1sa 或 1sb 作為粗糙的近似,可以把 Ψ 表示為 1sa 和 1sb 線性組合。
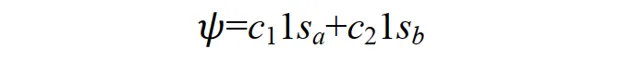
這種近似稱為分子軌域表示為原子軌域的線性組合,簡稱 LCAO 近似 (linear combination of atomic orbitals)。在原子結合成分子的過程中,電子運動波函數一般有較大的形變.如果像上式那樣僅用兩個原子軌域的線性組合來表示分子軌域,顯然是很粗糙的.為了提高精確度,應該用大量的原子軌域的線性組合來表示分子軌域 Ψ 。如開始的介紹中所說,我們用大量原子軌域定態方程式的解(原子軌域)為基函數擬合出了一個較精確的分子薛定諤方程式解(分子軌域)。其中組合系數 c1, c2, …可由變分法求得。因這種變分法的參數是線性組合系數,故稱為線性變分法。
如果每一個原子軌域都是其對應的 Schrödinger 方程式的精確解,則通常所有這些精確解構成一個完備系。下式的展開式中若包括無限多個原子軌域,則它所表示的分子軌域可以達到數學上嚴格精確的程度。在實際套用中,一般只取有限個原子軌域的線性組合,即LCAO近似。(關於變分法可以參考Levine書的第8章,講的非常好,雖然是英文的但很容易理解)
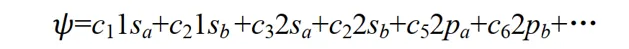
對於一個特定的分子軌域,展開式(4)中只有少數幾個原子軌域的貢獻是主要的。例如 CO 分子的一個占據電子的成鍵分子軌域,主要應由碳和氧原子的 2s 和 2p 軌域組合而成,其它原子軌域,如 1s, 3s,3p, 3d, 4s 等軌域對 CO 的成鍵貢獻應該是很小的。為了定性地討論問題,僅用碳和氧的 2s 和 2p 軌域組合起來,也許就能反映出 CO 成鍵的主要特征。同樣,對氫分子離子p+,對其共價鍵起主要作用的是氫原子的 1s 軌域,可以用兩個氫原子的 1s 軌域線性組合式(3)來定性地討論p+的成鍵問題。
這裏不厭其煩地弱弱插一句:線性組合,在元函數足夠多(直到構成相互正交完備集)的時候是趨近於嚴格精確的。只用兩個軌域的近似在數學上是非常粗暴不合理的,但事實證明這種簡陋的模型與實驗事實吻合得很好。一方面大大簡化了分析復雜度,一方面對討論問題的結論影響不大,因此這種方法很受歡迎。以後大家還會見到更粗暴的近似,沒錯,說的就是你HMO(休克爾分子軌域法)。
定義(1)中的Hamiltonian(哈密頓算符)為
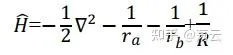
則(1)可轉化為
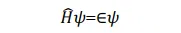
上式左乘 Ψ* 並對整個空間積分,得
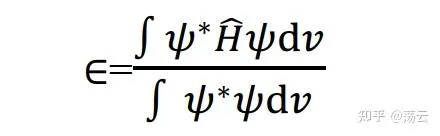
將(3)代入上式,則有
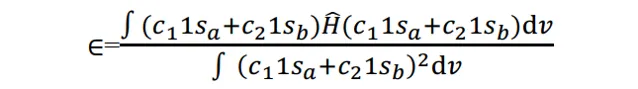
式(6)描述了這個體系的能量。我們要對它 做變分 , 使體系能量最低 ,求出各個組合系數c的值。
我們先把式(6)簡化一下,可定義以下四式。四個式子中,第一個和第四個是由於a核和b核是完全等價、可以互換的,所以能夠成立;第二三個是因為哈密頓算符的厄米性所以能夠成立(關於厄米性[Hermite]請參閱Levine書第7章)。
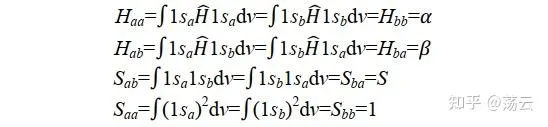
代入到(6)中
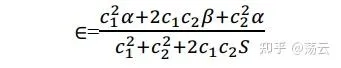
下面,按照變分原理,能量值最小時必須有
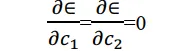
把(7)代入上式得到
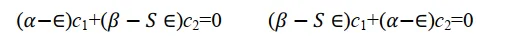
關於c1和c2的二元一次方程式組(8)有非零解的條件是系數行列式為零。 這是一個必須加入的附加條件。 上面這個方程式組出現0解即代表它對應的原子軌域不參與分子軌域組合,其權重為0,不符合問題的數學設定,也不符合物理。
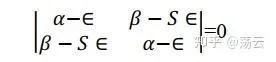
這個方程式稱為久期方程式,因其與描述行星的久期運動的方程式相似而得名。解得
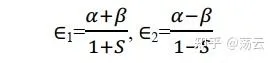
我們透過 解不為零 的性質拿到了最低能量可能值,現在回代方程式組(8)得到 c1=c2。
再加上一個附加條件:歸一化,即概率密度函數對全空間的積分必須等於1:
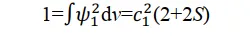
解出

所以首先解出 Ψ1,同理可解出Ψ2:
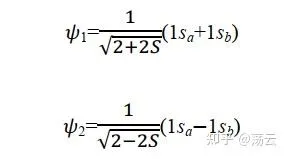
好的,現在我們已經取得了階段性的重要勝利:拿到了分子軌域波函數的具體(近似)形式。可以小結一下:氫分子離子是共價鍵的一個簡化模型,在其中不用考慮 電子互斥、自旋和全同性 的問題,只需要考慮兩個質子正電荷和一個電子構成的簡單系統中三者之間的相互作用。列出薛定諤方程式後,我們用LCAO近似的方法,首先將薛定諤方程式的解寫成原子軌域線性組合的方式,然後透過變分法求得組合系數,同時得到了兩個能量值和兩個分子軌域,即電子在整個分子體系中運動的波函數。這個過程中需要用到 組合系數不為零 以及 波函數歸一化 兩個預先設定好的條件。
我們再來看看我們拿到的結果。關於上面定義的 α、β 和 S 三個積分量,可以透過在橢球座標系中的積分求出。過程比較復雜(老實說作為學化學的我也不會),我就直接放結論:
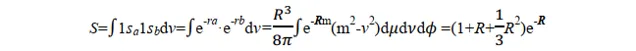
當核間距 R =0 時, S =1;當 R =∞時, S =0;當 0< R <∞時,1> S >0。實驗發現在p+的平衡構型下, R e=2 a.u. (a.u.為原子單位,是一個能量單位),由上式可得平衡構型下的 S e=0.586。可見 S 表示兩個軌域 1sa 和 1sb 的重叠程度,故 S 稱為重叠積分.圖 3.2 表示了兩個軌域 1sa 和 1sb 的重叠情況和重叠積分的大小.
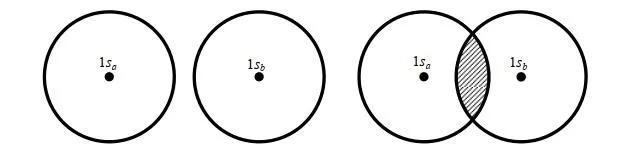
一種常有的錯誤認識是:原子軌域都是相互正交的,故 S 應恒為零。在這裏應強調:只有屬於同一個原子的原子軌域才是正交的;屬於不同原子的原子軌域,因其不是同一個 Hamiton 算符(是Hermite 算符)的固有函數,故它們並不相互正交。 正是不同原子的原子軌域間的重叠積分 S,才導致了共價鍵的形成 。(關於哈密頓算符及固有函數、完備函數域請參閱Levine書第7章)
關於α,則有
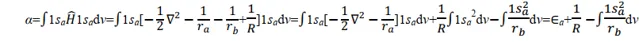
其中 Ea 為孤立的氫原子的基態能量,為 0.5 a.u.。1/ R 為核間排斥能; 在平衡構型下, R = 2a.u.; 1/ R =0.5a.u.。被積函數是1sa 態的電子與核 b 的吸引能。由此可見 α 主要與粒子間的 Coulomb 作用有關,故稱 α 為 Coulomb 積分,可用橢上式中積分項得到
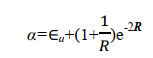
在平衡構型下 R e=2 a.u. ,可得
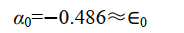
即 Coulomb 積分 α 與原子軌域能量 E a 近似相等
根據較復雜的橢球座標積分(這裏省略具體演算步驟,直接給出結果),可以得到
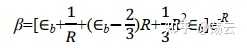
因為 Eb 是基態氫原子b的能量,其值為 -0.5 a.u.;故在平衡構型 R e=2 a.u.,得
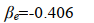
用 S e、 α e和 β e分別代入 E1和E2, 得到平衡構型下的能量為
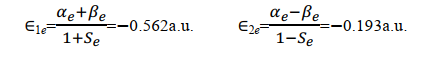
小結一下,透過求解積分值 S 、 α e和 β e我們得到了兩種原子軌域線性組合而成的分子軌域的波函數對應的能量本征值。根據式(18), β e為負值,所以式(19)中 E1<E2。註意,這裏用的都是原子單位制。
現在我們有了兩個波函數,如式(12)
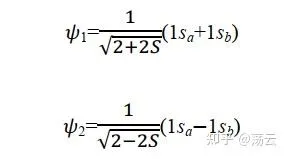
以及他們對應的平衡狀態能量
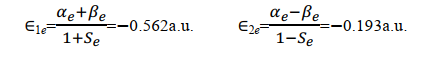
這即是兩個分子軌域,一個能量低,一個能量高。它們所描述的電子雲概率密度函數為

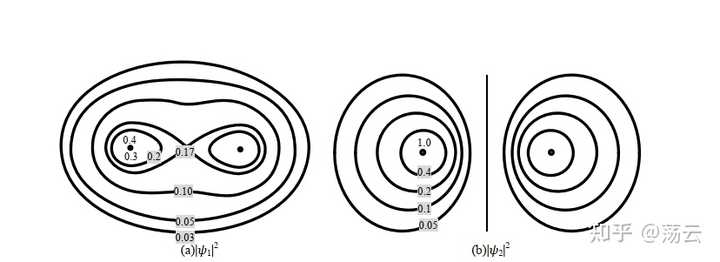
這是兩個三維概率密度函數,它們在Z方向的等高線圖如上。大家更熟悉的可能是同核sigma成鍵軌域和反鍵軌域的影像如下。註意, 這裏得到的並不是理論上嚴謹的分子軌域。 分子軌域法描述分子結構由於需要考慮多電子,還必須引入 Born-Oppenheimer 近似 和 非相對論近似 兩個基本近似。下圖僅做範例,讓大家把此處推導結果和已經學過的模型聯系起來。
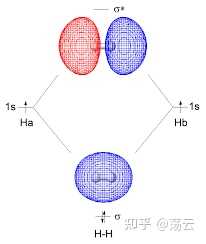
總結關於氫分子離子的討論,我們可以得到一些定性的結論:兩個原子軌域 1sa 和 1sb 的線性組合,可以得到兩個分子軌域 Ψ1 和 Ψ2 ,其中一個分子軌域的能量 E 1 低於其原子軌域的能量,這個分子軌域稱為成鍵軌域,另一個分子軌域的能量 E 2 高於其原子軌域的能量,這個分子軌域稱為反鍵分子軌域。在基態時,電子會占據能量低的成鍵軌域。註意,式(12)中兩個波函數的形式,可以視為分別為同相位疊加和不同相位抵消的結果,前面的1/根號部份可以看成一個歸一化因子。此外,分析ra=rb的情形就可以直觀地看出成鍵軌域兩原子中間的部份概率密度極大,而反鍵軌域該位置概率密度基本為0,形成節點。
可以把這個結論用能階圖直觀地表示出來.在平衡構型下, Coulomb 積分 α 近似地等於氫原子軌域能量 E a(或 E a),所以可用 α 表示原子軌域的能量,作為定性的直觀圖形表示,可忽略重叠積分 S。成鍵軌域能量和反鍵軌域能量分別為
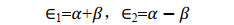
交換積分 β 小於零,所以能階圖應如下。兩邊為原子軌域的能階 α 中間為分子軌域的能階 E1 和 E2。 所謂成鍵三原則: 能量相近、最大重叠 和 對稱性匹配 中的前兩個根據上面的推導其實可以進行簡單直觀的數學解釋。最後一個對稱性匹配的問題需要借助一點群論的知識。雖然直觀看很簡單,但要給出一個可靠的普適性的解釋其實還是比較麻煩的。但這又是有機化學中重要的HMO(Huckel分子軌域法)的基礎。
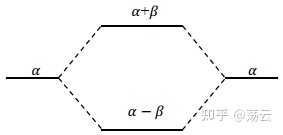
到此為止,分子軌域的基本推理方法已經簡單演示完了。應該基本可以比較嚴謹地回答題主的問題了。要用淺顯的話講明白一個這種包含大量數學推導的知識和理論好難啊。。。。
以後有空再更新多電子體系分子軌域的理論假設和電子填充規則。











