千萬不要小看PCA , 很多人隱約知道求解最大特征值,其實並不理解PCA是對什麽東西求解特征值和特征向量。 也不理解為什麽是求解特征值和特征向量。 要理解到Hinton對PCA的認知,需要跨過4個境界,而上面僅僅是第1個境界的問題。
為什麽要理解PCA?
其實深度學習在成為深度學習以前,主要是特征表達學習, 而特征表達學習追溯到始祖象階段,主要是無監督特征表達PCA和有監督特征表達LDA。 對了這裏LDA不是主題模型的LDA,是統計鼻祖Fisher搞的linear discriminant analysis(參考「Lasso簡史」)。 而Hinton在這方面的造詣驚人, 這也是為什麽他和學生一起能搞出牛牛的 t-Distributed Stochastic Neighbor Embedding (t-SNE) 。
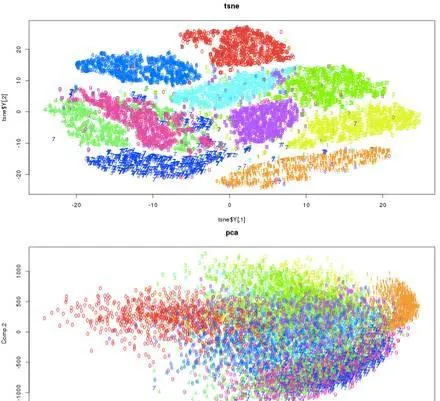
至於t-SNE為啥牛, 這裏給兩個對比圖片, 然後我們再回到PCA,以後有機會再擴充套件!
t-SNE vs PCA: 可以看到線性特征表達的局限性
t-SNE 優於 已有非線性特征表達 Isomap, LLE 和 Sammon mapping
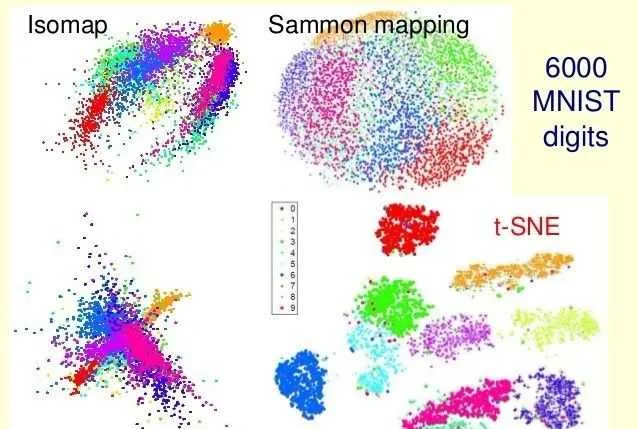
依然還記得2004年左右Isomap橫空出世的驚奇, 再看t-SNE的誕生,真是膜拜! 也正是Hinton對PCA能理解到他的境界, 他才能發明t-SNE。
PCA理解第一層境界:最大變異數投影
正如PCA的名字一樣, 你要找到主成分所在方向, 那麽這個主成分所在方向是如何來的呢?
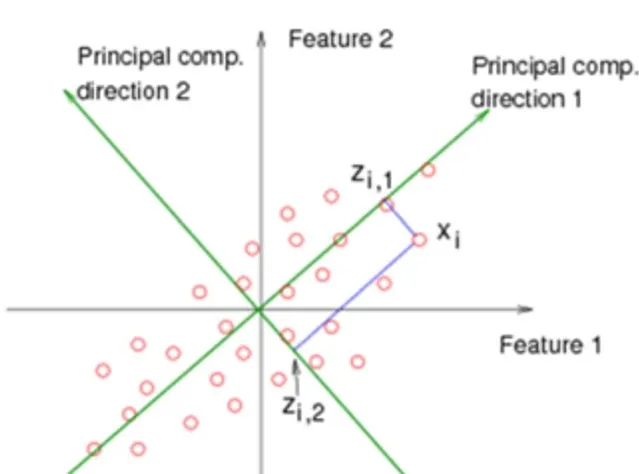
其實是希望你找到一個垂直的新的座標系, 然後投影過去, 這裏有兩個問題。 第一問題 : 找這個座標系的標準或者目標是什麽? 第二個問題 , 為什麽要垂直的, 如果不是垂直的呢?
如果你能理解第一個問題, 那麽你就知道為什麽PCA主成分是特征值和特征向量了。 如果你能理解第二個問題, 那麽你就知道PCA和ICA到底有什麽區別了。
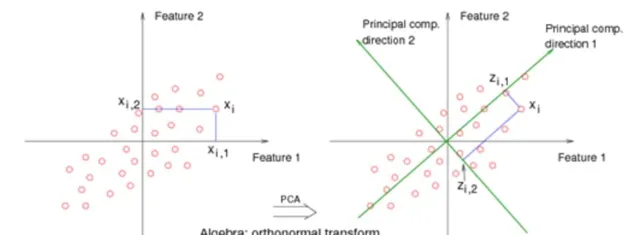
對於第一個問題: 其實是要 求解變異數最小或者最大 。 按照這個目標, 你代入拉格朗日求最值, 你可以解出來, 主成分方向,剛好是S的特征向量和特征值! 是不是很神奇? 偉大的拉格朗日 (參考 "一步一步走向錐規劃 - QP" "一挑三 FJ vs KKT ")

現在回答了,希望你理解了, PCA是對什麽東西求解特征值和特征向量。 也理解為什麽是求解的結果就是特征值和特征向量吧!
這僅僅是PCA的本意! 我們也經常看到PCA用在影像處理裏面, 希望用最早的主成分重建影像:

這是怎麽做到的呢?
PCA理解第二層境界:最小重建誤差
什麽是重建, 那麽就是找個新的基座標, 然後減少一維或者多維自由度。 然後重建整個數據。 好比你找到一個新的視角去看這個問題, 但是希望自由度小一維或者幾維。

那麽目標就是要最小重建誤差,同樣我們可以根據最小重建誤差推匯出類似的目標形式。

雖然在第二層境界裏面, 也可以直觀的看成忽略了最小特征值對應的特征向量所在的維度。 但是你能體會到和第一層境界的差別麽? 一個是找主成分, 一個是維度縮減。 所以在這個層次上,才是把PCA看成降維工具的最佳視角。
PCA理解第三層境界:高斯先驗誤差
在第二層的基礎上, 如果 引入最小平方法和帶高斯先驗的最大似然估計的等價性 。(參考"一步一步走向錐規劃 - LS" 「最小平方法的4種求解」 ) 那麽就到了理解的第三層境界了。
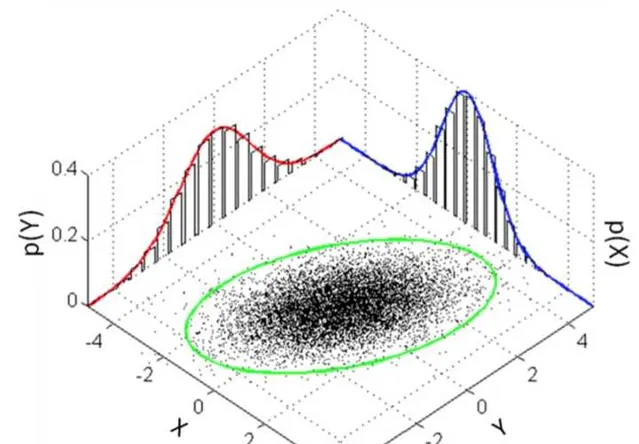
所以, 重最小重建誤差, 我們知道求解最小平方法, 從最小平方法, 我們可以得到高斯先驗誤差。

有了高斯先驗誤差的認識,我們對PCA的理解, 進入了概率分布的層次了。 而正是基於這個概率分布層次的理解, 才能走到Hinton的理解境界。
PCA理解第四層境界(Hinton境界):線性流形對齊
如果我們把高斯先驗的認識, 到到數據聯合分布, 但是如果把數據概率值看成是空間。 那麽我們可以直接到達一個新的空間認知。
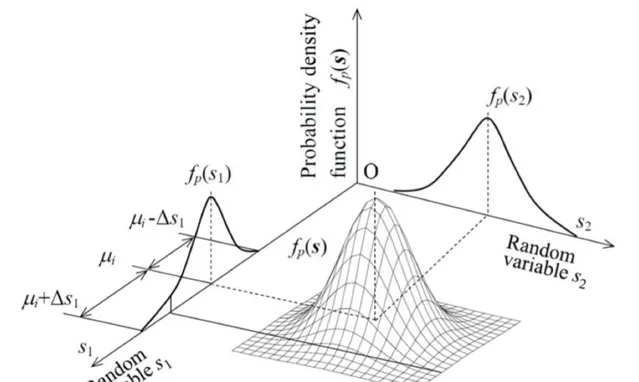
這就是「Deep Learning」書裏面寫的, 烙餅空間(Pancake), 而在烙餅空間裏面找一個線性流行,就是PCA要幹的事情。 我們看到目標函數形式和最小重建誤差完全一致。 但是認知完全不在一個層次了。
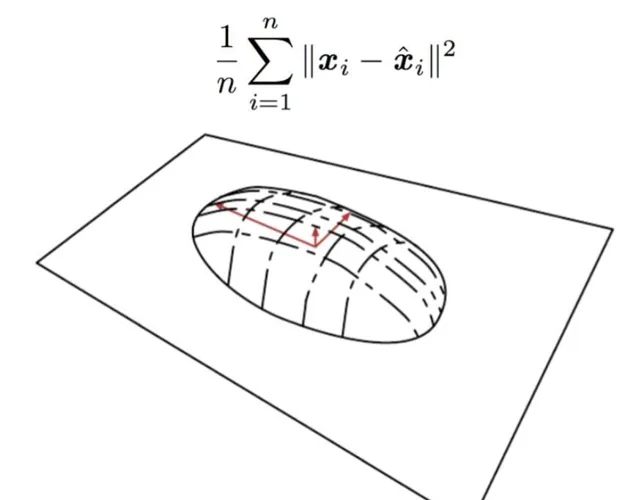
小結
這裏羅列理解PCA的4種境界,試圖透過解釋Hinton如何理解PCA的, 來強調PCA的重要程度。 尤其崇拜Hinton對簡單問題的高深認知。不僅僅是PCA,尤其是他對EM演算法的再認識, 誕生了VBEM演算法, 讓VB演算法完全從物理界過渡到了機器學習界(參考 「變の貝葉斯」)。 有機會可以看我對EM演算法的回答,理解EM演算法的8種境界。










