能科普下隨機圖理論嗎？

隨機圖模型

隨機圖的歷史

在 1959 和 1968 年期間，數學家 Paul Erdos 和 Alfred Renyi 發表了關於隨機圖（ Random Graph ）的一系列論文，在圖論的研究中融入了組合數學和概率論，建立了一個全新的數學領域分支---隨機圖論。

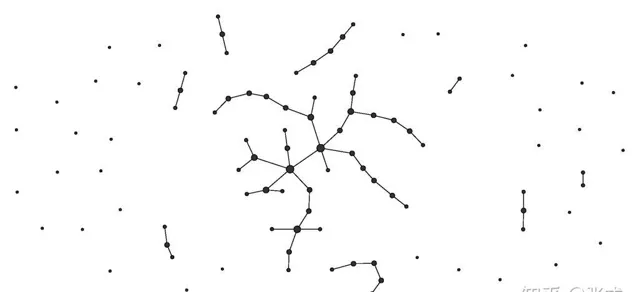
隨機圖的定義

本文只關註無向圖的場景。顧名思義， 隨機圖（Random Graph） 就是將一堆頂點隨機的連線上邊。好比在地上撒了一堆豆子，而豆子之間是否用線來相連是根據某個概率值來確定的。通常來說，對於隨機圖而言有兩種定義方式

1. 【定義一】給定 N 和 M, G_{1}(N,M) 的定義是隨機從 N 個頂點和 M 條邊所生成的所有圖集合中選擇一個。其中，這樣的圖集合的勢是 C(N(N-1)/2, M), 因此獲得其中某一個圖的概率是 1/C(N(N-1)/2, M).
2. 【定義二】給定 N 和 p ， G_{2}(N,p) 的定義是有 N 個頂點，並且兩個頂點之間以概率 p\in[0,1] 來決定是否連邊。

事實上，這兩個定義是等價的， N 個頂點的圖最多擁有的邊數是 N(N-1)/2, 而 G_{1}(N,M) 恰好有 M 條邊，並且它們分配的概率是均等的，因此兩個頂點之間是否存在邊的概率就是 p = M/(N(N-1)/2), 這裏的 C 指的是組合數。i.e.

G_{1}(N,M) = G_{2}(N, \frac{M}{N(N-1)/2}).

另一方面，對於 G_{2}(N,p) 而言，頂點兩兩之間是否存在邊的概率是 p, 而 N 個頂點的圖最多擁有 N(N-1)/2 條邊，於是邊數為 pN(N-1)/2. i.e.

G_{2}(N,p)=G_{1}(N,pN(N-1)/2).

進一步地，透過以上兩個公式可以得到：

G_{1}(N,M)=G_{2}(N,\frac{M}{N(N-1)/2}) = G_{1}(N,M).

在定義一中，可以直接算出所有頂點的平均度是 \langle k\rangle = 2 M /N. 但如果要計算圖的其余指標，用第二種定義 G_{2}(N,p) 反而更加容易，因此後續將會重點關註第二種定義，為方便起見，記號簡化為 G(N,p) = G_{2}(N,p).

隨機圖的度

圖的 度（degree） 指的是對於某個頂點而言，與它相關聯的邊的條數。對於隨機圖 G(N,p) 而言，它的邊數大約是 pN(N-1)/2, 最多與該節點相連線的頂點數為 N-1, 整個圖的頂點平均度是（邊數 * 2) / 頂點數，用記號 \langle k\rangle 來表示，意味著頂點平均度是 \langle k\rangle = p(N-1) \sim pN, 當 N 充分大的時候成立。換言之，

p \sim \langle k\rangle / N.

對於隨機圖 G(N,p) 中的一個頂點 i 而言，我們想計算它恰好有 d 條邊的概率值。事實上，對於除了 i 之外的 N-1 個點而言，有 d 個頂點與 i 相連， N-1-d 個頂點與 i 不相連，其概率是 p^{d}(1-p)^{N-1-d}, 同時需要從這 N-1 個點中選擇 d 個點，因此，頂點 i 的度恰好是 d 的概率是

p_{d}=C(N-1, d)\cdot p^{d}\cdot (1-p)^{N-1-d}.

特別地，當 d\ll N 時，上述概率近似於卜瓦松分布（Possion Distribution）。事實上， p=\langle k\rangle / (N-1) 並且

C(N-1,d) = (N-1)(N-2)\cdots(N-d+1)/ d! \sim (N-1)^{d} / d!,

(1-p)^{N-1-d} \sim (1-\langle k\rangle /(N-1))^{N-1-d} \sim e^{-\langle k\rangle},

因此，在 d\ll N 時， p_{d} 近似於卜瓦松分布，

p_{d} \sim \langle k\rangle^{d}e^{-\langle k\rangle}/d!.

隨機圖的連通分支

對於隨機圖 G(N, p) 而言，它的連通分支個數是與頂點的平均度 \langle k\rangle 息息相關的。特別地，當 \langle k\rangle=0 時，每個頂點都是孤立的，連通分支個數為 N; 當 \langle k\rangle=N-1 時，任意兩個頂點都有邊相連線，整個圖是完全圖，連通分支的個數是 1. 頂點的平均度從 0 到 N-1 的過程中，連通分支的個數從 N 演變到 1, 最大連通分支頂點數從 1 演變到 N, 那麽在這個變化的過程中，最大連通分支的頂點數究竟是怎樣變化的呢？是否存在一些臨界點呢？數學家 Erdos 和 Renyi 在 1959 年的論文中給出了答案：

對於隨機圖 G(N,p) 而言，用 N_{G} 表示最大連通分支的頂點個數，那麽對於圖的平均度 \langle k\rangle 而言，

1. 當 \langle k\rangle = Np < 1, 那麽 N_{G} = O(\ln(N));
2. 當 \langle k\rangle = Np = 1, 那麽 N_{G} = O(N^{2/3});
3. 當 \langle k\rangle = Np \in (1, \ln(N)), 那麽巨連通分支（Giant Component）存在，同時存在很多小的連通分支，在臨界點 1 的附近時， N_{G} \sim (p-p_{c})N, 這裏 p_{c}=1/N;
4. 當 \langle k\rangle = Np \in (\ln(N),+\infty), 那麽圖 G 是全連通圖，i.e. N_{G}=N.

在這個定理中，對於頂點的平均度 \langle k\rangle 而言，存在兩個臨界點，分別是 1 和 \ln(N). 當 \langle k\rangle < 1 時，巨連通分支不存在，所有連通分支的量級都在 O(\ln(N)) 以下；當 \langle k\rangle = 1 時，巨連通分支開始出現，量級大約是 O(N^{2/3}); 當 1<\langle k\rangle <\ln(N) 時，隨機圖存在一個巨連通分支和很多小的連通分支；當 \langle k\rangle > \ln(N) 時，圖是連通圖。

整個定理的證明有點復雜，但本文將會介紹 兩個臨界點 的計算。先來考慮第一個臨界點 \langle k\rangle = 1 的情況：

用 N_{G} 來表示隨機圖 G 中的最大連通分支的頂點個數， u 表示圖 G 中不在最大連通分支的頂點比例，i.e.

u=(N-N_{G})/N = 1 - N_{G}/N= 圖的頂點不在最大連通分支的概率。

對於不在最大連通分支的頂點 i 而言，其余的 N-1 個頂點分成兩種情況，Case（1）：要麽 i 與之不相連，此時概率是 1-p; Case（2）：要麽 i 與之相連，但此時的頂點不能在最大連通分支中，那就只能在剩下的 uN 個頂點中，其概率是 pu. 於是，對於所有頂點而言，它不在最大連通分支的概率是 (1-p+pu)^{N-1}. 於是，

u=(1-p+pu)^{N-1}=(1-p(1-u))^{N-1}.

根據 p\sim\langle k\rangle /N 和 \lim_{N\rightarrow +\infty}(1+x/N)^{N}=e^{x} 可以得到當 N 充分大時，有

u = (1-p(1-u))^{N-1} = (1-(1-u)\langle k\rangle /N)^{N-1} \sim e^{-(1-u)\langle k\rangle}.

令 s= 1-u = N_{G}/N, 它表示最大連通分支的頂點個數在所有頂點個數的占比，從而可以得到 近似方程式 ：

1-s=e^{-\langle k\rangle s}.

令 g(s) = 1 - s - e^{-\langle k\rangle s}, 則 g(0) = 0, g(1) = -e^{\langle k\rangle}<0. 它的導數是 g'(s) = - 1 + \langle k\rangle e^{-\langle k\rangle s}, 透過計算可以得到：

1. 當 \langle k\rangle \leq 1 時， g'(s)<0 在 (0,1) 上成立，i.e. g(s) = 0 在 [0,1] 上的唯一解是 s=0, 換言之， N_{G}/N = s \rightarrow 0;
2. 當 \langle k\rangle > 1 時，g'(s)>0 在 (0,\ln\langle k\rangle/\langle k\rangle) 成立， g'(s)<0 在 (\ln\langle k\rangle /\langle k\rangle,1) 成立。換言之， g(s)=0 在 [0,1] 上除了零之外還有解 s_{0}\in(0,1). 此時會存在巨連通分支， N_{G}/N = s_{0}\in (0,1) 是解。

因此，最大連通分支的頂點數在這個點會出現突變， 1 是該方程式的第一個臨界點，並且是出現巨連通分支的臨界點。

再來考慮第二個臨界點 \langle k\rangle = \ln(N) 的情況。對於極限狀況而言，假設僅有一個頂點不在最大連通分支中，那麽 s = N_{G}/N = (N-1)/N, 此刻，

1/N=1-s=e^{-\langle k\rangle s}=e^{-\langle k\rangle (N-1)/N},

兩邊求對數可以得到 \langle k\rangle = \ln(N), 因此，\ln(N) 也是一個臨界點，並且是出現全連通圖的臨界點。

隨機圖的六度分離

六度分離 又稱為 小世界現象 ，它的含義是在地球上任意選擇兩個人，他們之間最多相隔 6 個相識關系。換言之，來自世界上任何地方的兩個人都可以透過不超過 6 個相識關系所連線起來。

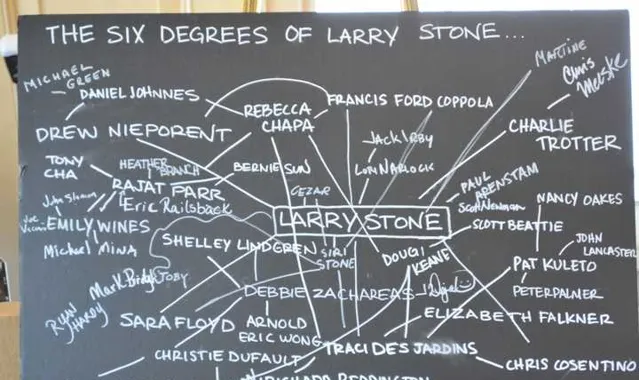
圖中兩個頂點的距離定義為兩個頂點之間的最短路徑長度，圖的直徑就是圖中任意兩點的距離的最大值。對於隨機圖 G(N,p) 而言，如果 \langle k\rangle \leq 1 則是不連通的，因此通常只需要考慮 \langle k\rangle>1 的情況，甚至只考慮 \langle k\rangle >\ln(N) 的全連通圖。任取一個頂點 i ，則有

1. \langle k\rangle 個距離為 1 的頂點；
2. \langle k\rangle^{2} 個距離為 2 的頂點；
3. \langle k\rangle^{3} 個距離為 3 的頂點；
4. \langle k\rangle^{d_{max}} 個距離為 d_{max} 的頂點；

同時，G(N,p) 而言，頂點的個數為 N, 這意味著 \langle k\rangle + \langle k\rangle^{2}+\cdots+\langle k\rangle^{d_{max}}\leq N. 透過等比級數的公式可以得到 \langle k\rangle^{d_{max}} \leq N, 因此，

d_{max} = O(\ln(N)/\ln(\langle k\rangle)).

而隨機圖的直徑的量級是與 d_{max} 成正比的，因此，隨機圖的直徑量級同樣是 O(\ln(N)/\ln(\langle k\rangle)). 如果 N = 10^9 並且每個人認識 \langle k\rangle = 200 個人，於是隨機圖的直徑量級是 \ln(6*10^9) / \ln(200) = 4.25 < 6.

參考文獻

1. Erdos Renyi Model：https:// en.wikipedia.org/wiki/E rdős–Rényi_model
2. Giant Component：https:// en.wikipedia.org/wiki/G iant_component
3. Erdős P, Rényi A. On the evolution of random graphs[J]. Publ. Math. Inst. Hung. Acad. Sci, 1960, 5(1): 17-60.
4. Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Reviews of modern physics, 2002, 74(1): 47.
5. 【巴拉巴西網絡科學】，艾伯特-拉斯洛·巴拉巴西（Albert-LászlóBarabási），2020.