我猜題主是想問高階微分的含義。二階導數寫成 \frac{\mathrm{d}^2y}{\mathrm{d}x^2} 這種形式確實跟高階微分有一定關系,但又有它的局限性。我在下面的解釋中會介紹無窮分階數體、高階微分的含義和完整形式、以及完整形式下高階微分的形式不變性等內容。看完就明白了。
首先,我們要搞清楚無窮小的概念。牛頓和萊布尼茨當年創立微積分時,都把無窮小當成一種數。他們的意思是, 無窮小是一種無限靠近0而又不是0的數 。但這個說法不夠精確,令人難以理解。他們有時把無窮小當作0舍去,有時又用無窮小來做分母,所以當時很多人搞不清楚無窮小到底和0有什麽區別,覺得無窮小是一種不可捉摸的東西。也正是因為這個原因,使得微積分在創立之初,便受到貝基利大主教等人的攻擊。
直到19世紀,德國數學家魏爾斯特拉斯提出ε-δ語言,才使無窮小得到了嚴格的定義。
定義 設函數f(x)在x0的某一去心鄰域內有定義(或|x|大於某一正數時有定義)。如果對於任意給定的正數ε(不論它多麽小),總存在正數δ(或正數X),使得對於適合不等式0<|x-x0|<δ(或|x|>X)的一切x,對應的函數值f(x)都滿足不等式
|f(x)|<ε,
那麽稱函數f(x)當x→x0(或x→∞)時為無窮小。
ε-δ定義也就是說:「如果x向x0奔跑時f(x)向0奔跑,那麽f(x)就是一個無窮小。」如果我們令f(x) = x,並令x0 = 0,那麽顯然f(x)滿足ε-δ定義,因此當x→x0時,f(x)是一個無窮小,或者說當x→0時,x是一個無窮小。這就是說,任何一個向0奔跑的變量都是一個無窮小。因此,ε-δ定義本質上是說: 無窮小是一個向0奔跑的變量 。
我們知道,變量之間可以具有函數關系。既然無窮小是一種變量,那麽無窮小之間也可以具有函數關系。設兩個無窮小x和y之間具有單調函數關系,那麽在它們向0奔跑的過程中,它們的取值是一一對應的。例如,當x = 0.12時,y可能等於0.08;當x = 0.06時,y可能等於0.002;等等。而我們真正關心的是,在x和y無限逼近0的過程中,它們的比例關系所趨向的極限。有以下四種情形:
●情形1:如果x/y→0,那麽x是y的「高階無窮小」,y是x的「低階無窮小」。此時,在向0奔跑的過程中,x在y面前變得越來越微不足道。打個比方,當y相當於一個西瓜大小時,x相當於一個核桃大小,當y縮小到核桃那麽大時,x已經縮小到一個細菌那麽大了。也就是說,越接近0,x和y的相對大小就越懸殊,並且這種懸殊差距會無限拉大。
●情形2:如果y/x→0,那麽x是y的「低階無窮小」,y是x的「高階無窮小」。此時,在向0奔跑的過程中,y在x面前變得越來越微不足道。
●情形3:如果x/y→B,其中B為非零常數,那麽x和y是「同階無窮小」。此時,在向0奔跑的過程中,x和y的比值趨向於常數B。
●情形4:如果x/y→1,那麽x和y是「等價無窮小」。這是同階無窮小的特例。此時,在向0奔跑的過程中,x和y的比值趨向於1。
也就是說,雖然我們考察的是變量向0奔跑的過程,但這只是一種輔助手段,我們真正關心的是兩個無窮小變量在奔跑終點處的比例關系。如果直接在奔跑終點處計算比例關系的話,那麽就是0比0,沒法計算,所以只能透過考察變量向0奔跑的過程來求極限處的比例關系。
既然x和y在向0奔跑的終點處可以具有比例關系,那麽x和y的奔跑終點應該不是0,而是一種無限靠近0的數。這樣一來,無窮小又成了牛頓和萊布尼茨描述的那種無限靠近0而又不是0的數。我們借助向0奔跑的變量,在這種不可捉摸的數之間建立起了比例關系,從而使得這種數互相之間可以定量地比較大小。這樣一來,這些數不再是不可捉摸的了,完全可以建立起一個新的數體來!
根據x和y的四種大小關系可以知道,這種無窮小數體中的數應該具有「階」和「權」兩個內容。例如,當x→0時,2sinx、3.5tanx、5x都是x的同階無窮小,它們的大小比例為2 : 3.5 : 5,而2(1-cosx)和 -2x^2 則都是x的高階無窮小。如果規定x是權值為1的一階無窮小,那麽2sinx、3.5tanx、5x分別是權值為2、3.5、5的一階無窮小,2(1-cosx)和 -2x^2 分別是權值為1和-2的二階無窮小, 6x^3 是權值為6的三階無窮小, 7x^{2.8} 是權值為7的2.8階無窮小。這些無窮小都是無限靠近0而又不是0的數。這樣,透過「階」和「權」這兩個內容,就建立起了一個無窮小數體,將所有的無窮小都包括了進來。
既然無窮小不是0,那麽它們可以取倒數。無窮小的倒數就是無窮大。如果規定x是權值為1的一階無窮小,那麽1/x、3.5/x、-2/x分別是權值為1、3.5、-2的一階無窮大,1/(1-cosx)是權為2的二階無窮大, 4.3/x^3 是權為4.3的三階無窮大, 2.2/x^{3.6} 是權值為2.2的3.6階無窮大。這樣一來,我們又得到一個無窮大數體,它可以和上述無窮小數體合並成一個數體。也就是說,把無窮大看作階為負數的無窮小,把無窮小看作階為負數的無窮大。
我們還可以把有限實數也包括到這個新數體中,也就是說,把實數看作0階無窮大或0階無窮小,而實數的數值就是它的權值。
這種新數體可以命名為「 無窮分階數體 」。因為其中的數都具有階和權兩個內容,所以可以用平面直角座標系來描述這個數體,如圖1所示。圖1中的點A到點H都代表無窮分階數體中的數,點A、B、C、D、E是無窮小,點F、G、H是無窮大。透過它們的縱座標和橫座標可以知道它們各自的階和權。
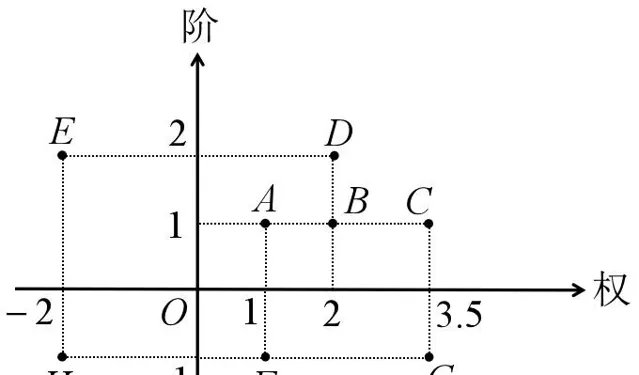
我們還可以建立起一套符號系統。將權值為 a 的m階無窮小記為 a(0)^m ,它也可以看成權值為 a 的-m階無窮大。將權值為 a 的m階無窮大記為 a(\infty)^m ,它也可以看成權值為 a 的-m階無窮小。
圖2左邊是一個邊長為1的正立方體,我們將它均勻地切成無窮多片,右邊展示了其中一片。那麽,每一片的體積可以規定為權值為1的一階無窮小,即 (0)^1 ,於是總片數就是權值為1的一階無窮大,即 (\infty)^1 。這無窮多片的體積之和,就是正立方體的體積。也就是說,權值為1的一階無窮小乘以權值為1的一階無窮大,結果為1,即
(0)^1\times(\infty)^1=1 。
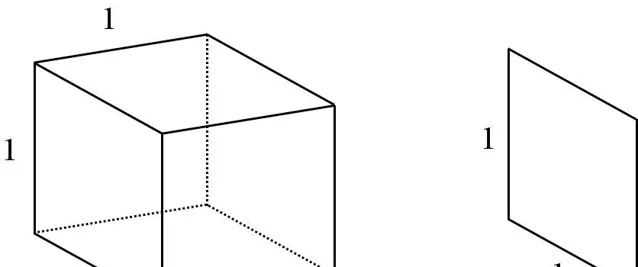
因為圖2中每一片的體積是權值為1的一階無窮小 (0)^1 ,所以如果將每一片再均勻切成無窮多條,如圖3左邊所示,那麽每一條的體積就是一個權值為1的二階無窮小,即 (0)^2 。因為總片數和每一片被切成的條數都是權值為1的一階無窮大,即 (\infty)^1 ,所以正立方體被切成的總條數是一個權值為1的二階無窮大,即 (\infty)^1\times(\infty)^1=(\infty)^2 。正立方體的體積等於這無窮多個切條的體積之和。也就是說,權值為1的二階無窮小乘以權值為1的二階無窮大等於1,即
(0)^2\times(\infty)^2 =1 。

如圖3右邊所示,如果繼續將每一條均勻切成無窮多塊,那麽每一塊的體積是權值為1的三階無窮小 (0)^3 ,正立方體被切成的總塊數是權值為1的三階無窮大 (\infty)^3 。這無窮多塊的體積之和,就是正立方體的體積。因此,權值為1的三階無窮小乘以權值為1的三階無窮大等於1,即
(0)^3\times(\infty)^3=1 。
因為無窮小是無限靠近0的數,所以有限值和無窮小相加時,無窮小不起作用。例如,圖2中正立方體的體積加上一個切片的體積,仍然等於正立方體的體積,即
1+(0)^1 = 1 。
類似地,低階無窮小和高階無窮小相加時,高階無窮小不起作用。例如圖3左邊,切片的體積是 (0)^1 ,將這個切片均勻切成 (\infty)^1 個切條,則每個切條的體積是 (0)^2 。如果給這個切片增加一個切條,那麽切片的體積並不會增加,即
(0)^1 + (0)^2 = (0)^1 。
類似地,無窮大和有限值相加時,有限值不起作用。例如,圖3左邊一個切片被分成 (\infty)^1 個切條,如果再加上一個切條,那麽總共還是 (\infty)^1 個切條,即
(\infty)^1+1=(\infty)^1 。
無窮小與實數0是不同的,因為一階無窮大個0加起來還是0,例如
0\times(\infty)^1 = 0 ,
而一階無窮大個一階無窮小求和卻得到一個有限值,例如
(0)^1\times(\infty)^1 = 1 。
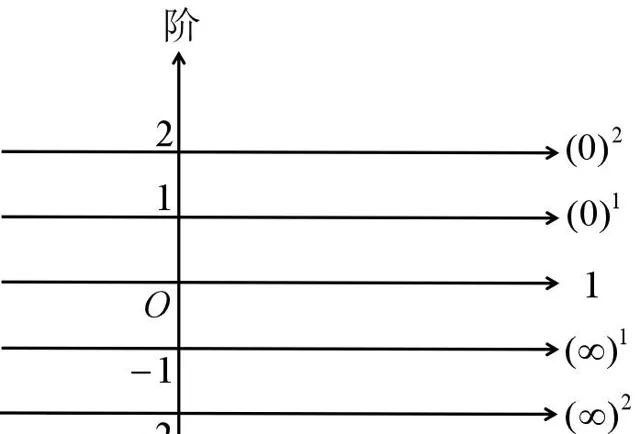
在圖1所示的無窮分階數體中,將相同階上的點連成數軸,便得到各階無窮大數軸和各階無窮小數軸,如圖4所示。這些數軸都與實數軸平行,且每一條數軸上的數都具有與實數類似的運算性質,只不過每一條數軸上的單位不同。例如,二階無窮大數軸上的數都以 (\infty)^2 為單位;一階無窮大數軸上的數都以 (\infty)^1 為單位;一階無窮小數軸上的數都以 (0)^1 為單位;二階無窮小數軸上的數都以 (0)^2 為單位;實數軸上的數都以1為單位,1也可以看作零階無窮大 (\infty)^0 或零階無窮小 (0)^0 。
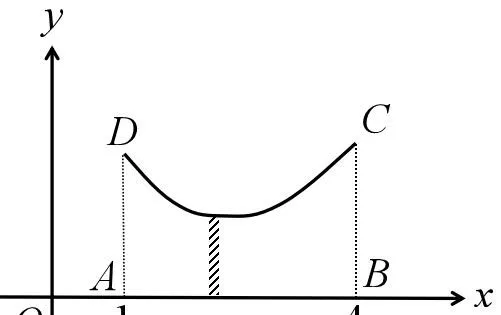
這樣,無窮小和無窮大都徹底變成了數,不僅可以進行它們的運算,而且還可以用它們來解釋定積分的含義。如圖5所示,如果想求曲線CD下方的面積,那麽可以將該面積切分成無窮多個豎直的窄條,然後再對所有窄條的面積求和。圖中陰影部份示意了其中一個窄條。如果認為每個窄條的寬度都相等,那麽可以規定每個窄條的寬度都是權值為1的一階無窮小,即 (0)^1 。於是每個窄條的面積都是一個一階無窮小,權值等於曲線CD上對應點的縱座標。因為這無窮多個窄條的寬度之和等於圖中點B和點A的x座標之差,也就是3,所以總共有 3/(0)^1 = 3(\infty)^1 個窄條,這是一個權值為3的一階無窮大。因此曲線CD下方的面積等於一階無窮大個權值互不相同的一階無窮小之和,這就是定積分的含義。
用無窮分階數體將無窮小和無窮大都變成數之後,接下來就可以研究微分和高階微分了。
我們都知道,微分是一種無窮小。設y=f(x),x=h(t),那麽當以x為自變量時,y的微分為
dy = f'(x)dx ;(1)
當以t為自變量時,x的微分為
dx = h'(t)dt ,(2)
y的微分為
dy = f'(x)h'(t)dt = f'(x)dx 。(3)
式(1)中的dx代表x自身的無窮小增量,而式(2)和式(3)中的dx則代表由t的無窮小增量引起的x的微分,即h'(t)dt。因此,在這三個式子中,dx具有兩種不同的含義。同理,dy也具有兩種不同的含義:式(1)中的dy代表由x的無窮小增量引起的y的微分,而式(3)中的dy則代表由t的無窮小增量引起的y的微分。
如果用ε-δ定義來理解無窮小,也就是將無窮小看成向0奔跑的變量,那麽式(1)和式(3)中的dy都是向0奔跑的變量,並且這兩個dy在向0奔跑的過程中一般是不相等的。同理,式(1)中的dx和式(3)中的dx在向0奔跑的過程中一般也是不相等的。但是式(1)和式(3)中的dy都可以表示成f'(x)dx這種形式,這種現象被稱作「微碎形式的不變性」。言外之意就是,微分的含義改變了,只是形式不變而已。
然而,式(1)中的dy和式(3)中的dy在向0奔跑的過程中,比值是趨向於1的,也就是說它們是等價無窮小。在奔跑到終點之後,作為無限靠近0而又不等於0的數,或者說作為無窮分階數體中的數,這兩個dy是完全相等的,具有相同的階和權。同理,式(1)中的dx和式(3)中的dx也是等價無窮小,它們到達奔跑終點後,也是無窮分階數體中相等的數,具有相同的階和權。這樣一來, 有了無窮分階數體之後,微分不光具有形式的不變性,而且具有了含義的不變性! 微分可以看作一階無窮小數軸上的數。在這個觀點下,任何一個變量的微分,都等於它自身的無窮小增量,與誰是自變量無關!
作為實數軸上的變量,x在每一個點處產生的微分dx都是一階無窮小數軸上的數,這些不同位置上的dx可以具有相同的權值,也可以具有不同的權值。如果不同點處的dx具有不同的權值,那麽dx就成為x的函數,例如可以設dx = u(x)(0)^1 。這樣一來,當x再次在各處產生無窮小增量時,作為x的函數,dx當然也會隨之產生無窮小增量,而這個無窮小增量很自然地就位於圖4中的二階無窮小數軸上。這就是x的二階微分 \mathrm{d}^2x 啊!
也就是說,變量的一階微分可以成為變量自身的函數。在此基礎上,一階微分的微分,就是變量的二階微分,它位於圖4中的二階無窮小數軸上。
再回過頭來看dy = f'(x)dx這個式子。當dx是x的函數時,dy也是x的函數。比如,當dx = u(x)(0)^1 時,dy = f'(x)u(x)(0)^1 。因此,當x再次在各處產生無窮小增量時,等式dy = f'(x)dx兩邊都隨之產生無窮小增量。根據微分的運演算法則d(uv) = vdu + udv,可知 \mathrm{d}^2y = d(dy) = d(f'(x)dx) = dxdf'(x) + f'(x)d(dx) = f''(x)\mathrm{d}x^2+f'(x)\mathrm{d}^2x 。因此有
\mathrm{d}^2y=f''(x)\mathrm{d}x^2+f'(x)\mathrm{d}^2x 。 (4)
這就是二階微分 \mathrm{d}^2y 的完整形式,它是具有形式不變性的!即使以t做自變量,存在x = h(t)這一層關系,等式(4)仍然是成立的!
傳統上,人們總是規定自變量在各處產生的微分相等。如果以x為自變量,規定dx在各處相等,那麽dx就成為一階無窮小數軸上的常數,從而 \mathrm{d}^2x = d(dx) = 0。這樣一來,等式(4)就變成了
\mathrm{d}^2y=f''(x)\mathrm{d}x^2 。 (5)
於是,等式(5)兩邊同除以 \mathrm{d}x^2 ,就得到了
f''(x) = \frac{\mathrm{d}^2y}{\mathrm{d}x^2} (6)
這個式子。
在數學分析教科書上,直接把等式(5)作為二階微分 \mathrm{d}^2y 的定義式,如圖6所示。並不只是某一個版本的數學分析教科書這樣寫,幾乎所有的數學分析教科書上都是這樣寫的。就連1958年出版的吉米多維奇的【數學分析習題集】裏,也是這樣定義高階微分的,如圖7、圖8、圖9所示。可見,這是一個傳統的定義。




但是顯然,這個定義是有局限性的,因為它只在「dx在各處相等」這個前提下成立,在一般情況下是不成立的。所以數學分析教科書上認為高階微分不具有形式的不變性。
問題就出現在「dx在各處相等」這個假設上。事實上,dx在各處完全可以不相等。如果以t為自變量,設x = h(t),並令dt在各處相等,不妨規定dt = (0)^1 ,那麽dx = h'(t)dt = h'(t)(0)^1 。顯然,此時dx在各處一般是不相等的。此時等式(5)不再成立,而等式(4)仍然成立。事實上,即使以t為自變量,也完全可以令dt在各處不相等,在這種情況下,等式(4)仍然是成立的。因此,等式(4)才是二階微分 \mathrm{d}^2y 的完整表達形式,它是具有形式不變性的。
數學分析教科書上之所以對高階微分采用了等式(5)這樣的有局限性的定義方法,是歷史遺留下來的問題。一方面,當年萊布尼茨祖師是這樣推導的。另一方面,自從魏爾斯特拉斯提出ε-δ語言後,無窮小就被當成向0奔跑的變量來研究了,而在這種框架下,想研究「微分的微分」是非常困難的。
因此二階導數寫成 \frac{\mathrm{d}^2y}{\mathrm{d}x^2} 這種形式,只能看成是一種歷史遺留下來的習慣。在這種習慣表達下, \frac{\mathrm{d}^2y}{\mathrm{d}x^2} 必須看作一個整體符號,上下不可拆分。如果要考慮二階微分 \mathrm{d}^2y 的獨立意義,那麽y對x的二階導數 f''(x) 應該表示為
f''(x) = \frac{\mathrm{d}^2y}{\mathrm{d}x^2} - \frac{\mathrm{d}y}{\mathrm{d}x}\frac{\mathrm{d}^2x}{\mathrm{d}x^2} 。 (7)
事實上,等式(7)和等式(4)是等價的。只需在等式(4)兩邊同除以 \mathrm{d}x^2 即可得到等式(7)。等式(7)中的\frac{\mathrm{d}^2y}{\mathrm{d}x^2} 和\frac{\mathrm{d}^2x}{\mathrm{d}x^2} 才是上下可拆分的。
順便說一句,高階微分同微分一樣,不僅具有形式的不變性,而且具有含義的不變性。關於無窮分階數體和高階微分的詳細研究,請看知乎文章【具有形式不變性的高階微分】:https:// zhuanlan.zhihu.com/p/70 866374
這篇文章更全面深入,不僅討論了高階微分在實際問題中的幾何意義,甚至還討論了直接由高階微分構成的微分方程式。
-----------------------------------------
補充說明兩點:
(1)我是昨天(2019年6月29日)才知道,原來早在1960年,德國數學家魯濱遜就嚴謹地提出了超實數體,並在此基礎上創立了「非標準分析」這個數學分支。我對非標準分析了解得還太少,目前僅憑從百度和知乎上搜到的描述性資訊來看,超實數體是一種將無窮小、無窮大與實數統一到一起的數體。單從這一點上來看,或許無窮分階數體就是超實數體的一種。超實數體和非標準分析是建立在嚴格的數學論證和一系列的定理基礎上的,好像有點像康托教授的集合論。相比之下,無窮分階數體則簡單又直觀。但是感覺上,無窮分階數體應該屬於非標準分析的範疇。
無窮分階數體和高階微分這套東西,是我在北航讀本科時冥思苦想搞出來的,當時是2002年末。這麽多年,我一直以為這是一個孤立的創造,現在看來是找到組織了。下一步準備拜讀一下魯濱遜的非標準分析著作,向組織靠攏。
(2)關於高階微分,我只能自不量力地呼籲一下,現有的數學分析教科書中那種不具有形式不變性的高階微分定義方法早該淘汰了。不具有形式不變性的高階微分,放在數學分析教科書中,簡直是一個敗筆。為了微積分的完整性和優美性,該為高階微分正名了。
---------------------
2019年7月7日補充:
(3)對無窮分階數體裏的運算律感興趣的同學,可以看看文章【具有形式不變性的高階微分】https:// zhuanlan.zhihu.com/p/70 866374 。其中有一節專門講運算律。這些運算律都是從微積分的計算中抽象出來的。在定積分中,略去高階項,只對最低階的無窮小進行累加,其原理就是「異階相加」這條運算律。
(4)有數學專業的同學指出,「無窮分階數體」裏的運算律,特別是「等價相減」,並不滿足數學裏對「域」的定義,所以不能叫做域。我想也許改稱「無窮分階數集」更合適。
2019年7月29日補充:
(5)萊布尼茨把二階導數寫為二階差商的極限。他對自變量 x 考察三個值: x 、 x_1=x+h 、 x_2=x_1+h ,對應的函數值分別為 f(x) 、 f(x_1) 、 f(x_2) . 記 h=\Delta x 、 y_1-y=\Delta y 、 y_2-y_1=\Delta y_1 . 記 (y_2-y_1)-(y_1-y) =\Delta y_1-\Delta y =\Delta(\Delta y)=\Delta ^2y . 那麽,二階差商為
\frac{1}{h}\left ( \frac{y_2-y_1}{h} -\frac{y_1-y}{h}\right) =\frac{1}{h^2}\left[ (y_2-y_1)-(y_1-y) \right] =\frac{\Delta ^2y}{(\Delta x)^2} .
從而二階導數為 f''(x)=\lim_{\Delta x \rightarrow 0}{\frac{\Delta ^2y}{(\Delta x)^2}} . (8)
在這個推導過程中,萊布尼茨將x在不同位置的增量都設為h,這也就是說,他將不同位置的dx看成是相等的,所以才得到了等式(8)。而「相等」是「不相等」的特例,因此只有假設不同位置的dx不相等,才具有一般意義。此時,該推導過程應該做如下修改。
對自變量x考察三個值: x 、 x_1=x+h 、 x_2=x_1+(h+\Delta h) . 也就是說,不同位置具有不同的增量:從 x 到 x_1 ,增量為 h ;從 x_1 到 x_2 ,增量為 h+\Delta h ,其中 \Delta h 是增量的增量。此時,二階差商為
\frac{1}{h}\left ( \frac{y_2-y_1}{h+\Delta h} -\frac{y_1-y}{h}\right) . (9)
根據 \frac{1}{x+\mathrm{d}x}-\frac{1}{x}=\mathrm{d}\left( \frac{1}{x} \right)=\frac{-1}{x^2}\mathrm{d}x 可知,當x位於分母上時,x的無窮小增量dx會使分式 \frac{1}{x} 產生無窮小增量 \frac{-1}{x^2}\mathrm{d}x 。也就是說, \frac{1}{x+\mathrm{d}x}=\frac{1}{x}-\frac{1}{x^2}\mathrm{d}x 。 將x換成h,將dx換成 \Delta h ,就得到當 \Delta h \to 0 時,
\frac{y_2-y_1}{h+\Delta h} \to (y_2-y_1)\left( \frac{1}{h}-\frac{1}{h^2}\Delta h \right) .
因此,當 \Delta h \to 0 時,式(9)所表示的二階差商趨向於
\frac{1}{h}\left ( (y_2-y_1)\left( \frac{1}{h}-\frac{1}{h^2}\Delta h \right) -\frac{y_1-y}{h} \right) ,
即 \frac{1}{h}\left ( \frac{y_2-y_1}{h} -\frac{y_1-y}{h} \right) -\frac{y_2-y_1}{h} \cdot \frac{\Delta h}{h^2} ,
即 \frac{\Delta ^2y}{h^2}-\frac{\Delta y_1}{h} \cdot \frac{\Delta h}{h^2} . (10)
因為 h=\Delta x ,所以 \Delta h=\Delta(\Delta x)=\Delta ^2 x ,從而式(10)即
\frac{\Delta ^2y}{(\Delta x)^2}-\frac{\Delta y_1}{\Delta x} \cdot \frac{\Delta ^2x}{(\Delta x)^2} .
於是,將二階導數表示為二階差商的極限,則立得
f''(x) =\lim_{\Delta x \to 0}{\left (\frac{\Delta ^2y}{(\Delta x)^2}-\frac{\Delta y_1}{\Delta x} \cdot \frac{\Delta ^2x}{(\Delta x)^2} \right)} =\lim_{\Delta x \to 0}{ \frac{\Delta ^2y}{(\Delta x)^2} } - \lim_{\Delta x \to 0}{ \frac{\Delta y_1}{\Delta x} } \cdot \lim_{\Delta x \to 0}{ \frac{\Delta ^2x}{(\Delta x)^2} } =\frac{\mathrm{d} ^2y}{\mathrm{d} x^2}-\frac{\mathrm{d} y}{\mathrm{d}x} \cdot \frac{\mathrm{d} ^2x}{\mathrm{d} x^2} .
可見,我們又一次得到了等式(7),這才是具有一般意義的二階導數運算式。
可能有同學對上式中的 \lim_{\Delta x \to 0}{ \frac{\Delta y_1}{\Delta x} } = \frac{\mathrm{d} y}{\mathrm{d}x} 感到疑惑。因為 \Delta y_1=y_2-y_1 ,所以按導數定義來講,應該是 \lim_{x_2 \to x_1}{ \frac{\Delta y_1}{x_2-x_1} } = \frac{\mathrm{d} y}{\mathrm{d}x} . (11)
但是註意到 x_1-x=h 和 x_2-x_1=h+\Delta h 都是無窮小,並且它們相差一個高階無窮小 \Delta h ,所以 x_1-x 和 x_2-x_1 是等價無窮小,所以式(11)中分母上的 x_2-x_1 可以用 x_1-x 替換。因此也有 \lim_{x_1 \to x}{ \frac{\Delta y_1}{x_1-x} } = \frac{\mathrm{d} y}{\mathrm{d}x} ,即 \lim_{\Delta x \to 0}{ \frac{\Delta y_1}{\Delta x} } = \frac{\mathrm{d} y}{\mathrm{d}x} .
註意這裏得到的 \frac{\mathrm{d} y}{\mathrm{d}x} 其實是點 x_1 處的導數值。但是因為當 \Delta x \to 0 時 x_1 \to x ,所以在導數連續的前提下,當 \Delta x \to 0 時,這個 \frac{\mathrm{d} y}{\mathrm{d}x} 也就趨向於點 x 處的導數值。











