谬误,目前空调是当前制冷方法中最科学最节能的,具体原因可以往下看看。
1、气体状态方程
先认识3个概念:
a)构成物质分子聚合状态称为物质的 聚集态 :气态、液态、固态、等离子态、超密态、BEC等;(液固为凝聚态)
b)没有外力作用,物理、化学性质完全相同,成分完全相同的均匀物质聚集态,称为 相;
c)处于平衡态的某种物质的热力学参量之间所满足的函数关系称为该物质的 状态方程 。
1.1理想气体
在压力极低时,分子间的距离非常大,此时分子间的相互作用非常小,而分子本身线度与分子间的距离相比可忽略不计,因此可将分子看作是没有体积的质点,这种状态下的气体可近似看作理想气体,理想气体在微观上具有以下两个特征:
①分子间无相互作用力;②分子本身不占有体积因此只有压强趋于零时的气体才是理想气体,理想气体可看作是真实气体在压力趋于零时的极限情况。对于理论上的理想气体 在任何温度、任何压力下均服从理想气体状态方程 。
玻意耳(Boyle, 1627-1691)定律: 物质的量和温度恒定时,体积与压强成反比
pV=C (1-1)盖·吕萨克(Gay Lussac, 1778-1850)定律: 物质的量与压强恒定时,体积与热力学温度成正比
V=V_{0}(1+\beta_{p}t) (1-2)
对于等压体膨胀系数,表示压强不变时单位温度所引起的体积变化
\beta_{p}=\frac{1}{V}(\frac{\partial V}{\partial T})_{p} (1-3)
式中 V 和 V_{0} 表示温度为 t 和 0℃ 的体积, \beta_{p}=1/273.15 ℃ ,热力学温度 T=(273.15+t/ ℃)K ,因此 V=V_{0}\beta_{p}T
\frac{V_{2}}{{V_{1}}}=\frac{T_{2}}{T_{1}} (1-4)查理(Charles, 1746-1823)定律: 物质的量与体积不变时,压强与热力学温度成正比
p=p_{0}(1+\alpha_{V}t) (1-5)
对于压强系数,表示体积不变时单位温度所引起的压强变化
\alpha_{V}=\frac{1}{p}(\frac{\partial p}{\partial T})_{V} (1-6)
式中 p 和 p_{0} 表示温度为 t 和 0℃ 的压强, \alpha_{V}=1/273.15 ℃ ,热力学温度 T=(273.15+t/ ℃)K ,因此 p=p_{0}\alpha_{V}T
\frac{p_{2}}{{p_{1}}}=\frac{T_{2}}{T_{1}} (1-7)以上实验得出的三个定律,归纳后可得出理想气体状态方程
pV=nRT (1-8)上式中 n 为物质的量,有些物理教材会用 \nu 代表。对于标准状况下 T=273.15K , p=1.013\times 10^{5}N\cdot m^{-2} , V_{m}=22.4\times 10^{-3}\ m^{3} ,带入上式得 普适气体常数
R=8.31J\cdot mol^{-1}\cdot K^{-1}对于混合理想气体,根据道尔顿定律: 混合气体的总压强等于各组分单独存在于混合气体的温度、体积条件下所产生压强的总和
p=\sum_{B}{p_{B}}=\sum_{B}\frac{n_{B}RT}{V} (1-9)
1.2真实气体
理想气体分子没有相互作用,所以在任何温度、压力下都不会液化。但真实气体分子间相互作用势能随分子间距离的变化类似引力势能变化。降低温度与增加压力可使气体的摩尔体积减小,即 分子间距离减少,这将使分子间相互吸引力作用增加,导致气体变成液体 。
在某一适当温度下,液体与其蒸汽可达成一种动态平衡,即单位时间内由液体分子变为气体分子的数目与由气体分子变为液体分子的数目相同,也就是说液体的蒸发速度与气体的液化速度相同,此时这种气-液平衡时的气体称为饱和蒸汽,所具有的压强称为 饱和蒸气压 p^{*} 。当饱和蒸气压与外界压力相等时,液体沸腾,此时相应的温度称为液体的 沸点 。我们先来看看3种常见物质的饱和蒸气压
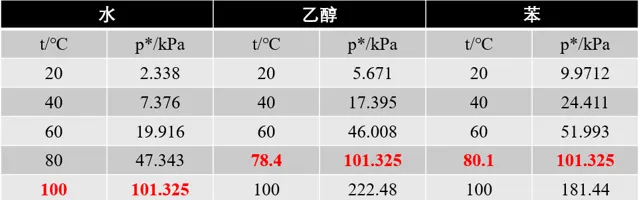
图中标红的数据为标准大气压下的正常沸点,根据道尔顿定律,此时无论空气中该物质组分所占含量,即便空气中水蒸汽含量达到100%,但已达到饱和蒸气压,液体表面的分子会发生汽化,内部的分子也会汽化。在一定温度下如果蒸汽分压小于饱和蒸气压,液体将蒸发,直到蒸发至蒸汽分压升至饱和蒸气压;反之,如果蒸汽分压大于饱和蒸气压,气体将液化,直到液化至蒸汽分压降至饱和蒸气压。例如,水在20℃时饱和蒸气压2.338kPa,但只要水蒸气的分压小于2.338kPa,液体就会蒸发,这就是衣服能在常温下自然晾干的原因;夜晚降温时,饱和蒸气压降低,空气中水蒸汽分压大于饱和蒸气压,因此液化出现露珠。
液体的饱和蒸气压随温度的升高而增大,从理想气体状态方程也可以看出,温度升高若要使体积不变,则压强越大。但对于真实气体,有一个特殊的温度, 在该温度以上,无论施加多大压强,都不再能使气体液化 ,这个温度称为 临界温度 T_{c} ,临界温度是气体能够液化所允许的最高温度。
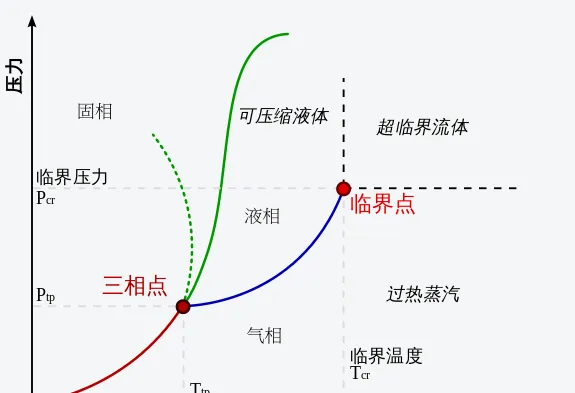
给定一种组成,通过实验可以发现在特定温度及压强下只有某些相可以存在,把这些相在不同压强和温度时的实验结果绘制成 相图 。在临界温度 T_{c} 时对应的饱和蒸气压称为 临界压力 p_{c} ,也就是与相图中液气共存线段的交点,称为 临界点 。当温度及压力接近临界点时,液相和气相的性质会越来接近,在临界点时无法区分液相和气相,温度及压强一旦超过临界点,就没有单独可区分的液相或气相,只会有一种称为超临界流体的流体相。超临界流体可以理解为一种稠密的气相,其具有气体的黏度与液体的密度,扩散系数比液体大得多,再加大压强就不属于工程上研究的问题了。


在相图中我们还可以看到左下方有一个使一种物质三相达到热力学平衡共存时的一组温度和压强数值,这就是 三相点 ,在这个温度和压强附近,一点点扰动就会使物质发生沸腾或凝固,变得非常不安定。比如,水 的固-液-气-三相点是0.01℃ (273.16K )及611.73Pa (约等于标准大气压101.325kPa 的千分之六)。在上面的动图中我们可以看出三相点左下方,物质是可以轻易发生气-固转变的,比如沸腾的气泡突然凝固,冻结的固体突然涨裂。反之,现实中有些自然升华和凝华的物质,其实在高温高压下也是有液体状态的。
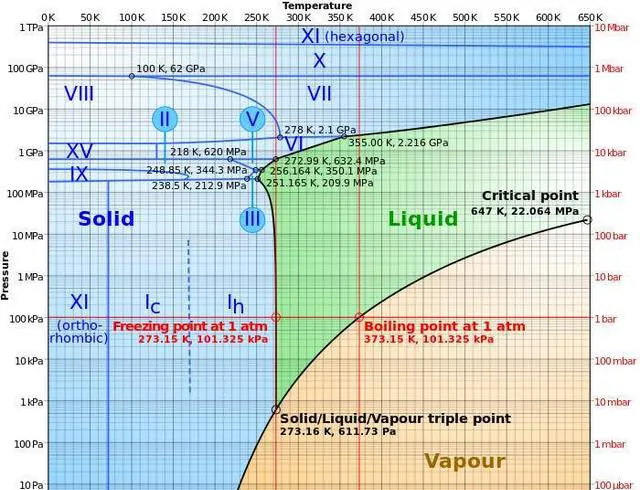
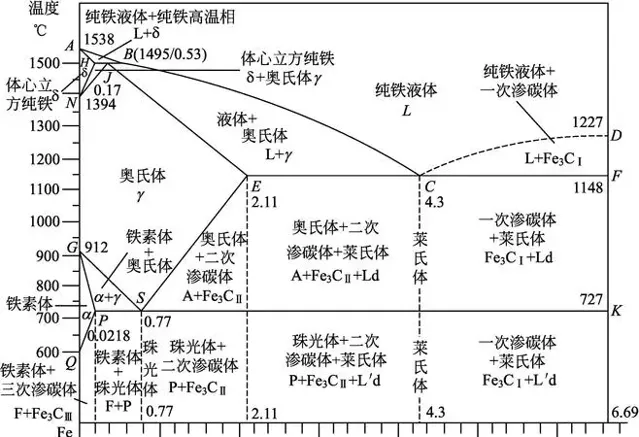
上面仅仅针对的是水而言,但是如果物质有多种固相和液相,测相图上相邻的相之间都会形成三相点。许多固体(如铁、冰)在不同温度和压力下会有不同的固相,因此有多个三相点。如冰有正交晶系和六方晶系等9种晶体结构,铁在冷却过程中会经历 \delta 体心立方、 \gamma 面心立方、 \beta 体心立方、 \alpha 体心立方相变,如果是两相共存还要参考铁碳相图,过程会更加复杂。不过,氦 -4是唯一有两种液相(低温下液氦发生二级相变 )的物质,所以氦-4虽然没有固-液-气-三相点,但有液-液-气-三相点:2.177 K, 5.043 kPa。
范德华(van der Waals) 认为理想气体的压强是指分子间无相互作用力时的压强,摩尔体积是每摩尔气体分子自由活动的空间;而真实气体处在实际的p,Vm,T条件时,由于分子间有相互作用,压力p实际上是理想气体在同等T,Vm时所应有的压强减去由于内部吸引力造成的压强减小后的结果,即 p=p_{理}-a/V_{m}^{2} ;而体积在考虑了分子本身占有的体积b后,自由活动的空间 V_{m自由}=V_{m}-b ,因此将修正后的压强和体积带入理想气体状态方程
(p+\frac{a}{V_{m}^{2}})(V_{m}-b)=RT (1-10)上式为范德华方程,将 V_{m}=V/n 代入上式
(p+\frac{an^2}{V_{}^{2}})(V_{}-nb)=nRT (1-11)得到适用于其物质的量为n的范德华方程,式中的a,b为范德华常数。经过范德华修正后,真实气体也有自己的状态方程了。

1.3微观模型
热力学第零定律 (Zeroth Law of Thermodynamics)也称为热平衡定律:
若两个热力学系统均与第三个系统处于热平衡状态,此两个系统也必互相处于热平衡。说明白一点就是热0给出了温度的概念(互为热平衡的物体间温度相同),因此建立了共同的热力学温标。
伯努利(Daniel Bernoulli, 1700—1782)设想气体压强来自例子碰撞器壁所产生的冲量。任何宏观可测定量均是某微观量的平均统计值,所以器壁所受到的气体压强是单位时间内大数分子频繁碰撞器壁所给予单位面积器壁的平均总冲量。这种碰撞是无间歇的,所施加的力也是恒定不变的,在这里给出微观气体压强公式,n为分子数量
p=\frac{1}{6}n\tilde{v}\cdot2m\tilde{v}\approx\frac{1}{3}nm\tilde{v^{2}} (1-12)同样可以计算出分子的平均动能
\bar{\varepsilon_{t}}=\frac{1}{2}m\bar{v^{2}} (1-13)值得一提的是,气体压强不仅存在于器壁,也存在于气体内部,对于理想气体,这两种压强表达式完全相同。我们将微观量与宏观量进行联系,可得到 玻尔兹曼常数k
k=\frac{R}{N_{A}}=1.38\times10^{-23}[J\cdot K^{-1}]
最后将微观与宏观表达式进行联系p=nkT,可得 单原子 分子热运动平均动能
\bar{\varepsilon_{t}}=\frac{3}{2}kT (1-14)摩尔内能则为
U_{m}=N_{A}\cdot\frac{3}{2}kT=\frac{3}{2}RT (1-15)上式表明分子热运动平均平动动能与绝对温度成正比,绝对温度越高,分子热运动越剧烈。绝对温度是分子热运动剧烈程度的量度, 粒子的平均热运动动能与粒子质量无关,而仅与温度有关 。 \bar{\varepsilon_{t}} 是分子杂乱无章热运动平均平动动能(内能),它不包括整体定向运动动能(机械能)。
2、功与热,焓与熵
先记住3个定义:
a)热力学中对于功与热这种 过程量 取变分而不取微分,如 đW、đQ(物理化学教材里用δW、δQ),而对于内能、焓、熵这种 状态量 取微分而不取变分,如 dU、dH、dS,我们可以不用纠结数学上的定义,在这里只是借用两种符号区别一下这几种量纲[J]相同的物理量。
b)只有系统内部各部分之间及系统与外界之间都始终同时满足力学、热学、化学平衡条件的过程才是 准静态过程 。
c)只有无耗散的准静态过程才是 可逆过程 。
2.1热力学第一定律
功是在力学相互作用过程中系统和外界之间转移的能量 。热力学中的力学相互作用力是一种广义力,它不仅包括机械力(压强、拉力、表面张力等),也包括电场力、磁场力等,所以功也是一种广义功,这里有4点需要注意:
1)只有在系统状态变化过程中才有能量转移,系统处于平衡态时能量不变,因而没有做功, 功与系统状态无对应关系,说明功不是状态量 ;
2)只有在广义功作用下产生了广义位移后才做了功;(如压强、电动势在体积变化和电荷量迁移后)
3)非准静态过程中,由于系统内部压强处处不同,且随时在变化,很难计算系统对外做的功,因此 系统对外做功计算局限于准静态过程 ;
4)外界对气体做 功 以 W 表示,气体对外界做功以-W表示。
气体对外界做功以体积膨胀形式进行,此时对气体分析有đW=-pdV,该过程是无限小的可逆过程中外界对气体所做元功的表达式,它是系统状态量p、V的函数。đW>0,表示外界对系统做正功,此时dV<0表示气体被压缩,反之则膨胀。在整个可逆过程中有
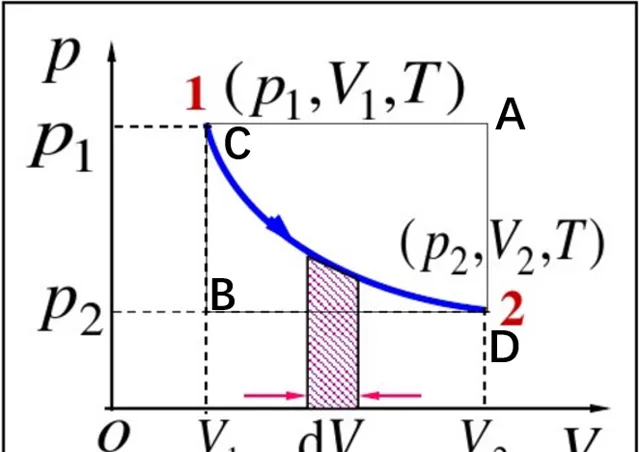
W=-\int_{V_{1}}^{V_{2}}pdV (2-1)表示外界对系统做的总功。上述过程存在的问题是同时存在2个自变量T=T(p,V),实际上并不用重积分,只需令每一种准静态变化过程都对应于p-V图中某一曲线,这时p与V就有一一对应关系。另外,在下图中可以发现沿CD等温线,沿CAD先等压再等体,沿CBD先等体再等压,三条曲线下的面积均不相等,这说明功与变化的的路径有关,功不是系统状态属性,不是状态函数,元功đW不满足多元函数中全微分条件。 đW仅表示沿某一路径的无穷小变化,因此在微分符号d上加一杠đ以示区分 。
等温过程:
W=-\int_{V_{1}}^{V_{2}}pdV=-nRT\int_{V_{1}}^{V_{2}}\frac{dV}{V}=-nRTln\frac{V_{2}}{V_{1}}=-nRTln\frac{p_{2}}{p_{1}} (2-2)等压过程:
W=-\int_{V_{1}}^{V_{2}}pdV=-p\int_{V_{1}}^{V_{2}}dV=-p(V_{2}-V_{1}) (2-3)等体过程:
W=-\int_{V_{1}}^{V_{2}}pdV=0 (2-4)当系统状态的改变来源于热学平衡条件的破坏,也即来源于系统与外界间存在温度差时,我们就称系统与外界间存在热学相互作用,有能量从高温物体传递给低温物体,这样传递的能量称为 热量Q 。热量和功是系统状态变化中伴随发生的两种不同的能量传递形式,是不同形式能量传递的量度,它们都 与状态变化的中间过程有关,因而不是系统状态的函数 。
与功一样,一个无穷小过程中所传递的热量只能写成đQ而不是dQ,因为不满足多元函数全微分条件。功与热量的区别在于它们分别来自不同的相互作用: 功由力学相互作用引起,只有产生广义位移时才伴随功的出现;热量来源于热学相互作用,只有存在温差时才有热量传递 。此外,热力学中还有化学相互作用,扩散、渗透、相变、溶解稀释、化学反应等都属于这种。
热力学第一定律 (First Law of Thermodynamics)其推广和本质就是著名的 能量守恒定律 :
物体内能的增加等于物体吸收的热量和对物体所做的功的总和。这里的 内能U 是系统内部所有微观粒子的微观无序运动能以及总的相互作用势能两者之和。 内能是状态函数 ,处于平衡态系统的内能是确定的,内能与系统状态间有一一对应关系。热1的数学表达式也就是 内能定理 ,内能的增加可来源于外界对系统做功W与从外界吸收的热量Q
U_{2}-U_{1}=Q+W (2-5)对于无限小的过程,因为U是状态函数,能满足多元函数全微分条件
dU=đQ+đW (2-6)对于准静态过程,结合(2-1)可得出
dU=đQ-pdV (2-7)如此一来,我们就把功、热量、内能和理想气体的状态方程联系起来了。最后要注意一点 理想气体 内能是温度的函数U=U(T),与体积压强无关。但对于 真实气体U=(T,V),内能还是V的函数 ,所以气体向真空自由膨胀时势能增加(理想气体无势能),动能降低,温度是会降低的。
dU=(\frac{\partial U}{\partial T})_{V}dT+(\frac{\partial U_{ }}{\partial V})_{T}dV (2-8)2.2热力学第二定律
功和内能都能通过宏观或微观的数学表达式定义出来,对于同为过程量的热量,我们可以用热容进行描述。物体升高或降低 单位温度 所吸收或放出的热量称为物体的 热容C
C=đQ/dT (2-9)每摩尔物体的热容称为 摩尔热容Cm ,有C=nCm单位质量物体的热容称为 比热容c ,有C=mc。
在等体过程中,气体与外界没有功的交往,所吸收的热量全部用来增加内能,因此 摩尔定体热容 C_{V,m} 为
C_{V,m}=(\frac{\partial U_{m}}{\partial T})_{V} (2-10)在等压过程中,吸收的热量除用来增加内能外,还需使气体膨胀对外做功,所以定压比定体热容大 。根据(2-7)可知đQ=dU+pdV(克劳修斯的热1表达式),为了计算摩尔定压热容 C_{p,m} ,我们定义一个函数
H=U+pV (2-11)因为U、p、V都是状态函数,故它们的组合 焓H 也是状态函数,与内能和热容类似,把h、Hm称为比焓和摩尔焓,因此摩尔定压热容 C_{p,m} 为
C_{p,m}=(\frac{\partial H_{m}}{\partial T})_{p} (2-12)等压过程中吸收的热量等于焓的增量 。由于 C_{p,m} 和 C_{V,m} 的定义,可导出两者的关系
C_{p,m}-C_{V,m}=(\frac{\partial H_{m}}{\partial T})_{p}-(\frac{\partial U_{m}}{\partial T})_{V}=(\frac{\partial H_{m}+pV_{m}}{\partial T})_{p}-(\frac{\partial U_{m}}{\partial T})_{V}=(\frac{\partial U_{m}}{\partial T})_{p}+p(\frac{\partial V_{m}}{\partial T})_{p}-(\frac{\partial U_{m}}{\partial T})_{V}
根据(2-8) dU_m=(\frac{\partial U_m}{\partial T})_{V}dT+(\frac{\partial U_{ m}}{\partial V_m})_{T}dV_m ,在等压时除以dT得
(\frac{\partial U_m}{\partial T})_{p}=(\frac{\partial U_m}{\partial T})_{V}+(\frac{\partial U_{ m}}{\partial V_m})_{T}(\frac{\partial V_m}{\partial T})_{p} ,代入 C_{p,m}-C_{V,m} 式中得
C_{p,m}-C_{V,m}=[(\frac{\partial U_{ m}}{\partial V_m})_{T}+p](\frac{\partial V_m}{\partial T})_{p} ,我们可以这样看 (\frac{\partial U_{ m}}{\partial V_m})_{T}(\frac{\partial V_m}{\partial T})_{p} 相当于1mol物质等压升温1K时,体积膨胀克服分子间吸引力,从外界吸收的热量, p(\frac{\partial V_m}{\partial T})_{p} 相当于体积膨胀对外界做功而吸收的热量。
对理想气体状态方程有 (\frac{\partial V_m}{\partial T})_{p}=\frac{R}{p} , (\frac{\partial U_{ m}}{\partial V_m})_{T}=0 ,代入上式,最终有迈耶公式
C_{p,m}-C_{V,m}=R (2-13)关于热量的描述过程可以结合热1表达式,đQ=n C_{V,m} dT+pdV,来描述等温、等压、等体过程
等温过程: 理想气体内能不变đQ=-đW=pdV
Q=-W=nRTln\frac{V_2}{V_1} (2-14)等压过程: 吸收热量为đQ=n C_{p,m} dT
Q=n\int_{T_{1}}^{T_{2}}C_{p,m}dT (2-15)等体过程: 系统对外界做功为零,吸收的热量等于系统内能的增加đQ=n C_{V,m} dT
Q=n\int_{T_{1}}^{T_{2}}C_{V,m}dT (2-16)值得注意的是,等压过程中其内能改变量与等体过程吸收热量相同 U_1-U_2=n\int_{T_{1}}^{T_{2}}C_{V,m}dT 。同为过程量的功在等体过程可以不变化,那么热量也存在一种过程可以不变化,这就是绝热过程。
绝热过程: Q=0,系统绝热膨胀对外做了多少功,内能就减少多少。由đQ=n C_{V,m} dT+pdV,可知
-pdV=n C_{V,m} dT (2-17)我们对理想气体状态方程两边全微分pdV+Vdp=nRdT,有dT=(pdV+Vdp)/nR,代入(2-17),得 ( C_{V,m} +R)pdV=- C_{V,m} Vdp, 结合(2-13),并定义 \gamma=\frac{C_{p,m}}{C_{V,m}} ,最终化简为 \frac{dp}{p}+\gamma\frac{dV}{V}=0 ,解微分方程可得
p_1V_{1}^{\gamma}=p_2V_{2}^{\gamma}=···=C (2-18)\gamma 称为 比热容比 或 绝热指数 ,是一个联系微观与宏观的系数。进一步我们有
\gamma=\frac{C_{p}}{C_{V}}=\frac{H}{U}>1 ; C_{p,m}=\frac{\gamma R}{\gamma-1} ; C_{V,m}=\frac{ R}{\gamma-1} (2-13.5)热力学第二定律 (Second Law of Thermodynamics)的表述和推广定理很多,也称为熵增定律:
开尔文(Kelvin):不可能从单一热源吸收热量,使之完全变为有用功而不产生其他影响;克劳修斯(Clausius):不可能把热量从低温物体传到高温物体而不产生其他影响;
实质:在一切与热相联系的自然现象中它们自发地实现的过程都是不可逆的。
功能自发地、无条件地全部转化为热;但热转化为功是有条件的,而且转化效率有所限制,也就是说功自发转化为热折一过程只能单向进行而不可逆。热1说明了自然界中能量是守恒的(宏观上),不会凭空产生,热2则说明从单一热源吸热全部用来做功是不可能的,热机效率不可能提高到100%,且存在其他理论极限,本文将在下节展开。

2.3卡诺定理
热力学第一、第二定律都是在一次次失败制作永动机的尝试中总结出来的。在真实的 热力循环中(指系统或工作物质从初态出发经历一系列的中间状态最后回到原来状态的过程 ),工作物质从高温热源吸热所增加的内能不能全部转化为对外做的有用功,它必须向外放出一部分热。
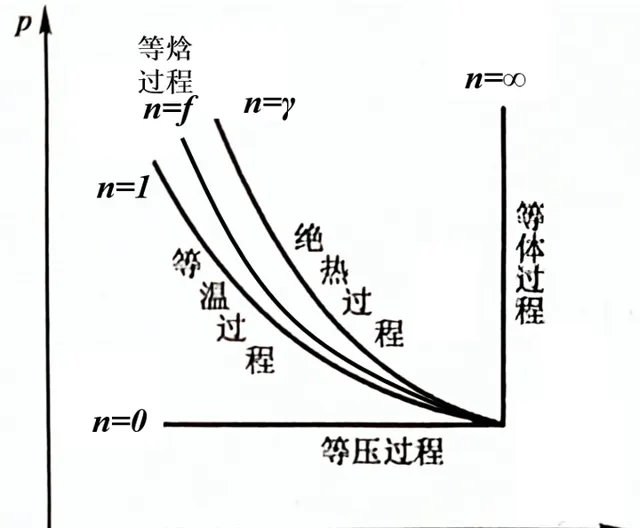
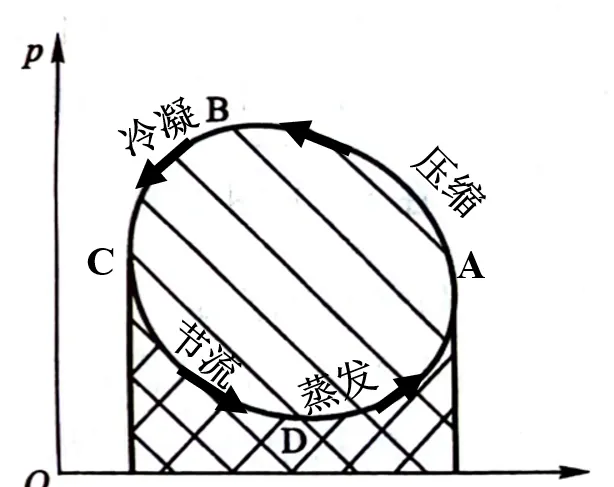
在上述准静态热机循环图中,A→B过程温度升高,内能增加,对外做功,属于吸热过程;B→C过程温度降低,内能减少,对外做功,属于放热过程;C→D过程温度降低,内能减少,外界对系统做功,属于放热过程;D→A过程温度升高,内能增加,外界对系统做功,属于吸热过程。横坐标V轴正方向为对外做功,反方向系统对内做功;纵坐标p轴正方向为吸热,反方向为放热。我们还可以发现:
1)热机由热驱动,热比功多,因此是吸热和升温等价,放热和降温等价;
2)A→B→C过程的系统对外做功减去C→D→A过程的外界对系统做功,循环净功就是p-V图循环曲线围成的面积;
3)顺时针循环表示系统从高温热源吸热,向低温热源放热,系统对外界做净功,此为热机;
我们可以推出: 逆时针循环表示系统从低温热源吸热,向高温热源放热,外界对系统做净功,此为冷机 。
我们用循环中 吸收的总热Q1 及 放出的总热Q2 计算热机的理论效率
\eta_热=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1} (2-19)我们已经知道要使热机循环,在经历温度升高、体积增加后必须要使温度降低、体积减小才能回到初始状态,而绝热过程没有系统与外界热量交换,是一个理想的循环阶段,因此在计算理论效率时必须有两个绝热过程(对外和对内做功)。根据现有理想气体过程可以推导出3种理想循环:卡诺循环(等温)、奥托循环(等体)、狄赛尔循环(等压)。
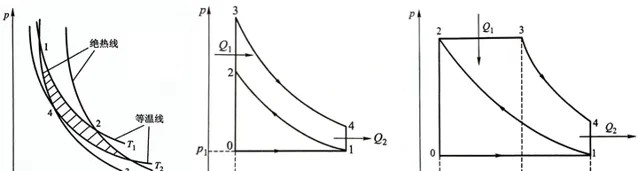
对于卡诺循环:
1、恒温可逆膨胀(1→2)有 Q_1=-W_1=nRT_1ln\frac{V_2}{V_1} , \Delta U_1=0 ;
2、绝热可逆膨胀(2→3) W_2=\Delta U_2=nC_{V,m}(T_2-T_1) ;
3、恒温可逆压缩(3→4) Q_2=-W_3=nRT_2ln\frac{V_4}{V_3} , \Delta U_3=0 ;
4、绝热可逆压缩(4→1) W_4=\Delta U_4=nC_{V,m}(T_1-T_2) ;
整个过程系统对外界做功 -W=-(W_1+W_2+W_3+W_4)=nRT_1ln\frac{V_2}{V_1}+nRT_2ln\frac{V_4}{V_3} ,根据绝热过程(2-18)的关系有 \frac{V_2}{V_3}=\frac{V_1}{V_4}=(\frac{T_2}{T_1})^\left( 1/(\gamma-1) \right) ,所以有 \frac{V_2}{V_1}=\frac{V_3}{V_4} ,所以 -W=nR(T_1-T_2)ln\frac{V_2}{V_1} ,根据热机效率定义
\eta=\frac{-W}{Q_1}=\frac{nR(T_1-T_2)ln\frac{V_2}{V_1}}{nRT_1ln\frac{V_2}{V_1}}=1-\frac{T_2}{T_1} (2-20)结论有:
①卡诺热机热效率仅与两个热源的温度有关,温差越高效率越大;
②因为-W=Q1+Q2,有 \frac{Q_1+Q_2}{Q_1}=\frac{T_1-T_2}{T_1} ,进一步有\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0 (2-21)
③ 卡诺循环可逆,当循环逆向进行时η不变,外界对系统做功,把热从低温物体转移到高温物体 。
其余两种循环在这里仅做参考,效率都是和体积有关,用于内燃机更合适
奥托循环: \eta_{otto} =1-(\frac{V_1}{V_2})^\left(1-\gamma \right)
狄赛尔循环: \frac{V_1}{V_2}=K ,\frac{V_3}{V_2}=\rho , \eta_{diesel} =1-\frac{\rho^\gamma -1}{\gamma(\rho-1)K^{\gamma-1}}
卡诺循环中两个绝热可逆过程的功相同,而两个恒温可逆过程的功不同,气体恒温可逆膨胀时因过程可逆是的热机对外做功最大,而恒温可逆压缩时因过程可逆使系统从外界得功最小,故一个循环过程的总结果是热机以极限的做功能力向外界提供了最大可用功,因而其效率时最大的。我们可以将其抽象为卡诺定理:
(1)在相同的高温热源和相同的低温热源间工作的一切可逆热机其效率相等,与工作物质无关;(2)在相同高温热源与相同低温热源间工作的一切热机中,不可逆热机效率不可能大于可逆热机效率。
效率:100%>可逆>不可逆
在得到卡诺定理后,我们开始建立一个新的状态函数 熵S 。对于一个无限小的卡诺循环,工质只从热源吸收或放出热đQ,结合式(2-21),
\frac{đQ_1}{T_1}+\frac{đQ_2}{T_2}=0
即任何卡诺循环的可逆热温商之和为零。因过程量是可逆的,T是系统的函数恒不为0(热3),在极限情况下有
\oint_{卡}^{ }\frac{đQ}{T}=0 (2-22)即任意可逆卡诺循环的可逆热温商 \frac{đQ}{T} 沿封闭曲线的环路积分为0(没有奇点)。变量全微分的闭环路积分为零(保守场),反过来闭环路积分为零,所积变量为某函数的全微分。该变量的积分只取决于系统的始末状态,因此为状态函数
dS=đQ/T (2-23) 可逆时,对于 一般过程有dS≥đQ/T(克劳修斯不等式)结合热1,đQ=dU+pdV可得
TdS=dU+pdV (2-24)因đQ是广延量,T是强度量,因此熵S也是广延量,但摩尔熵Sm时强度量。由于T>0,所以系统可逆吸热đQ>0时,熵是增加的;系统可逆放热,熵是减小的,单位[J/K]。为了计算熵,可用热容表示
C_V=(\frac{đQ}{dT})_V=T(\frac{\partial S}{\partial T})_V ; C_p=(\frac{đQ}{dT})_p=T(\frac{\partial S}{\partial T})_p
对于理想气体 dU=n C_{V,m} dT , 有dS= n C_{V,m} dT/T+nRdV/V ,进行T0到T的积分
S-S_0=nC_{V,m}ln\frac{T}{T_0}+nRln\frac{V}{V_0} (2-25)同理有
S-S_0=nC_{p,m}ln\frac{T}{T_0}-nRln\frac{p}{p_0} (2-26)熵增加原理:热力学系统从一平衡态绝热到达另一个平衡态的过程中,它的熵永不减少。
3、节流膨胀
理想模型在前面2章已经铺垫的差不多了,接下来我们加快速度进入具体的原理阶段。
3.1能量均分
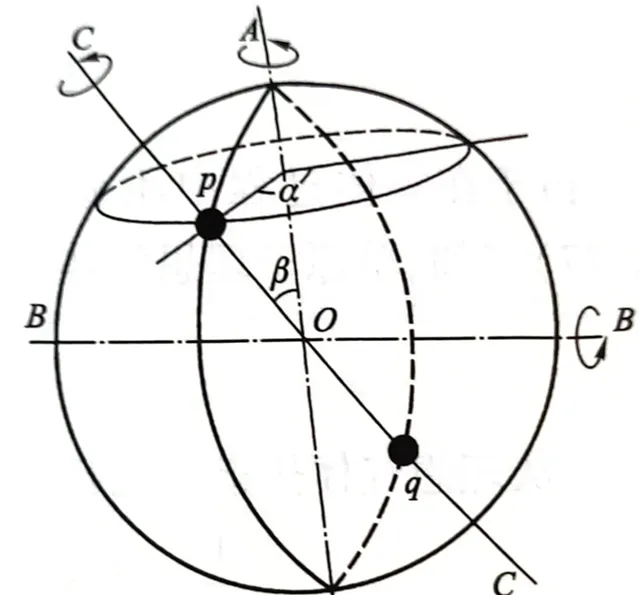
之前推导比热容比γ的时候,也把这个系数称为绝热指数,这个数不仅仅是推导过程中用来简化方程的书写,还与很多真实气体的分子类型有关。对于单原子理想气体,只有热运动动能没有势能,由分子热运动平均动能式(1-14) \bar{\varepsilon_{t}}=\frac{3}{2}kT ,以及理想气体热运动无择优取向 \frac{1}{2}m\bar{v^{2}_x}=\frac{1}{2}m\bar{v^{2}_y}=\frac{1}{2}m\bar{v^{2}_z}=\frac{1}{3}\cdot\frac{1}{2}m\bar{v^{2}} 可知
\frac{1}{2}m\bar{v^{2}_x}=\frac{1}{2}m\bar{v^{2}_y}=\frac{1}{2}m\bar{v^{2}_z}=\frac{kT}{2} (3-1)单原子理想气体的摩尔等体热容为(1-15)和定体热容定义
C_{V,m}=\frac{3}{2}R (3-2)上式说明在理想气体中,xyz三个方向的平均平动动能都均分为kT/2。但是这一规律用来解释双原子及多原子气体时,与实验结果并不相符。

这是因为双原子以上分子的分子结构不再能简化成质点,必须把它们当成刚体。若要解释单原子与多原子理想气体热容的差异,必须引用力学中自由度的概念。若一刚体在空间平动,又以各种可能转动,因此需要3个平动、3个转动自由度。对于双原子分子,原子的质量集中在半径 10^{-15} m的原子核上,而分子线度(化学键长度)为10^{-10} m,它绕自己化学键中心轴旋转的转动惯量仅为绕另外两轴的10^{-10} 而可忽略,因此双原子分子又3个 平动自由度 和2和 转动自由度 。
若非刚性分子,相邻两原子间相对位置还可改变,原子间作用可使其振动,所对应的自由度为 振动自由度 。非刚性双原子分子有一个沿两质心连线振动的振动自由度,因此其自由度为6个。
N个原子组成的多原子分子自由度最多为3N个一般来说 ,在这3N个自由度中,有3个平动、3个转动、3N-6个振动自由度。不过例外还是挺多的,振动一般都比较多,比如双原子、直线三原子分子都是这样。
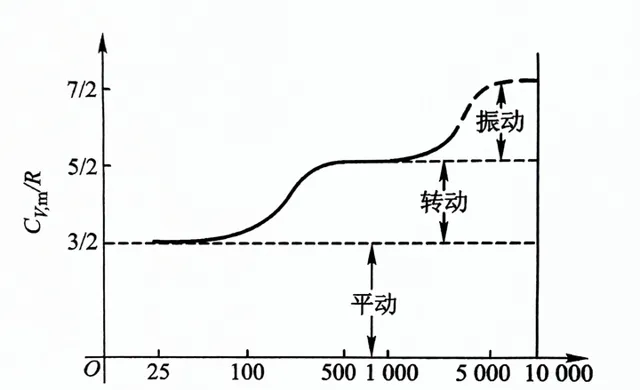
接下来把单原子理想气体的平均平动动能推广到多原子。单原子分子理想气体的3个平均平动动能分到3个平动自由度中,每个自由度均分到kT/2平均动能,那么我们也可以认为每一转动及振动自由度也均分kT/2平均动能,有
处于温度T的平衡态气体中,分子热运动动能平均分配到每一个分子的每一个自由度上的平均动能都是kT/2 。对于振动能量除动能外还有振动势能,由于分子中原子所进行的振动都是振幅非常小的微振动,可以看作简谐振动。一个周期内,简谐振动的 平均动能 与 平均势能 相等,所以 一个振动自由度均分kT的能量 。若某种分子有t个平动自由度、r个转动自由度、v个振动自由度,则每一分子的总的平均能量为
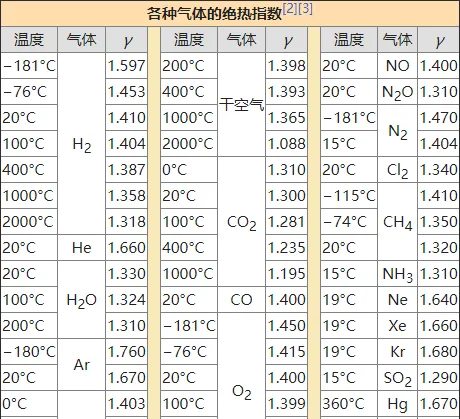
\bar{\varepsilon}=(t+r+2v)\cdot\frac{1}{2}kT=\frac{1}{2}ikT (3-3)其中的 i=t+r+2v,表示的是分子的自由度 。需要强调的是,上式中的各种振动、转动自由度都应是确实在对能量均分定理作全部贡献的自由度,因为自由度会发生「冻结」。在常温下 O_2 N_2 H_2 CO H_2O 等都是刚性分子,振动自由度被冻结,(只计算平动和转动,双原子=3+2,多原子=3+3)O_2 N_2 H_2 CO 的自由度i=5,水蒸气H_2O 的自由度i=6。能量均分定理不仅适用于理想气体,一般也可用于液体和固体,只不过凝聚态是通过分子间很强的相互作用来实现。
分子自由度和绝热指数的关系有 γ=1+2/i ,比如常温下不考虑振动,对于单原子i=3,γ=1.67;双原子i=5,γ=1.4;多原子i=6,γ=1.33。
3.2传热方式
热量传递有三种基本方式:热传导、热对流与热辐射。
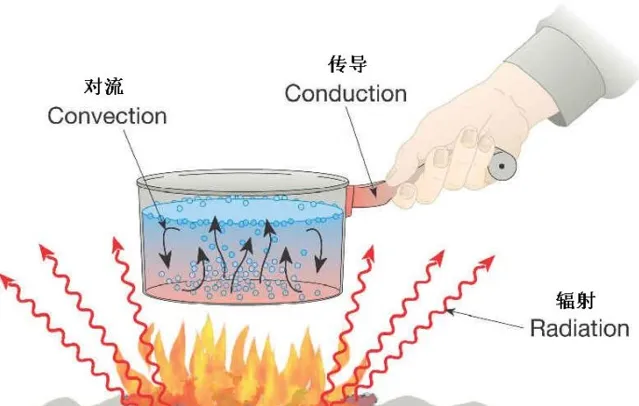
热传导 (Heat Conduction):是指在物体内部或相互接触的物体表面之间,由于分子、原子及自由电子等微观粒子的热运动,而产生的热量传递现象,是热能 从高温向低温部分转移的过程,是一个分子 向另一个分子传递振动能 的结果。主要通过傅立叶定律描述,主要有热通量密度 {\display style {\overrightarrow {q}}} ,单位 W·m^{−2} , 热导率k(热导率为在单位时间内,每单位截面积所流过的热量除以单位距离温度变化量的负值) ,单位 W·m^{−1}·K^{−1} ,温度梯度 {\display style {\big .}\nabla T{\big .}} ,单位K·m^{−1} 组成。
{\display style {\overrightarrow {q}}} =-k{\display style {\big .}\nabla T{\big .}} (3-4)热对流 (Heat Convection):是指由于流体 的宏观运动而引起的流体各部分之间发生相对位移(对流 ),冷热流体相互掺混所引起的热量 传递过程。对流传热可分为强迫对流和自然对流。强迫对流,是由于外界作用推动下产生的流体循环流动。自然对流是由于温度不同密度 梯度变化,重力作用引起低温高密度流体自上而下流动,高温低密度流体自下而上流动。对流传热其经验公式为牛顿冷却定律,主要有流入或损失的热量q,单位W,传热系数h(单位时间内通过单位面积传递的热量),单位 W/(m^2K) ,传热面积A,单位m²,固体表面与周围流体的温度差△T,单位K。也可以忽略热源面积将hA等效为α,称为热适应系数。
q=-hA\Delta T (3-5)热辐射 (Thermal Radiation)是物体用电磁辐射 把热能 向外散发的热传 方式,以热辐射传递热时 不需要介质 。任何物体温度只要高于0K就会释放热辐射。热辐射功率可以表示为
P_{rad}=\epsilon\sigma AT^4 (3-6)这里只有两个未知量,其中 斯特藩常数 可以用玻尔兹曼常数表示,单位[ Wm^{-2}K^{-4} ],物体表面放射率 {\display style \epsilon } 介于0~1之间,黑体辐射为1。
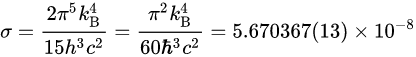
3.3焦耳-汤姆孙效应
在制冷过程中,我们计算效率时要考虑的是从低温热源吸走的总热量Q2,那么外界必须对制冷机做功W,系统向高温热源放出的热量为Q1,有 \eta_冷=\frac{Q_2}{W}=\frac{Q_2}{Q_2-Q_1} 。我们继续逆时针卡诺循环,同样可得出
\eta_{卡冷}=\frac{T_2}{T_2-T_1} (3-7)可以看出制冷温度越低时,制冷系数也越小,当T2为绝对零度时,则制冷系数为0。这里补充一下
热力学第三定律 (Third Law of Thermodynamics)又常被称为 能斯特定理(Walther Hermann Nernst):
能斯特表述:系统的熵在等温过程中的改变随绝对温度 趋于0。普朗克表述:在绝对 零度时,一切完美晶体的熵 值等于0。
推论:不可能通过有限的步骤使物体温度降低到绝对零度。
1852年焦耳 James Prescott Joule 和汤姆孙(开尔文勋爵, Kelvin Lord )发现气体 会因在 等焓 的环境下膨胀,而使温度上升或下降(基本上都是下降)。我们之前推导过等温、等压、等体、绝热过程,我们这里的绝热都是可逆的,那也可以称为等熵过程,现在还差一个等焓过程,这里参考理想气体的等某过程
等焓热容C_H=\left( \frac{\delta Q}{\partial T} \right)_H
dH=dU+pdV+Vdp=\delta Q+Vdp
在等焓过程中 dH=\delta Q+Vdp=0
\left(\frac{\delta Q}{\partial T} \right)_H=-V\left( \frac{\partial p}{\partial T} \right)_H=-nR
C_H=-nR (3-8)等焓热容是个负值,这意味着在等焓过程中温度升高系统反而会对环境放热 。
根据广义泊松方程(多方过程),等焓过程有
p_1V_{1}^{f}=p_2V_{2}^{f}=···=C (3-9)其中 f=2-1/γ,显然可知f<γ ,至此所有等某过程介绍完毕。
我们回头看JT的实验。如果系统隔热效果好或者过程发生进行得很快,系统来不及和外界发生明显的热量交换,那我们也可以用绝热过程近似分析。在这种绝热条件下,高压气体经过多孔塞流到低压一边的稳定流动过程称为 节流过程 。工业上常通过使气体通过 节流阀 或 毛细管 来实现 节流膨胀 。

节流膨胀过程绝热,所以Q=0。过程的功由两部分组成,左侧活塞运动至多孔塞的过程中,环境对系统做功 W_1=p_1V_1 ,右侧活塞由多孔塞处移动至末态位置时,系统对环境做功 W_2=-p_2V_2 ,故整个节流膨胀过程功 W=p_1V_1-p_2V_2 ,根据热1,有 U_1-U_2=p_1V_1-p_2V_2 ,整理得 U_1+p_1V_1=U_2+p_2V_2 ,即
H_2=H_1 (3-10)所以节流膨胀时等焓过程。对于真实气体节流膨胀后不仅温度会变化,压强也要变化(不然无法自发进行),因此焓H(T,p)是T,p的函数,为描述气体节流膨胀制冷或制热能力的大小,引入如下焦耳-汤姆孙系数,又称 节流膨胀系数, 以下简称JT系数
\mu_{JT}=(\frac{\partial T}{\partial p})_H (3-11)我们对H(T,p)进行全微分 dH=(\frac{\partial H}{\partial T})_pdT+(\frac{\partial H}{\partial p})_Tdp=C_pdT+(\frac{\partial H}{\partial p})_Tdp , C_pdT 相表示理想气体的焓变, (\frac{\partial H}{\partial p})_Tdp 表示气体的非理想性带来的附加贡献,可以解释为要克服分子间作用力而必须施加的功。
根据循环定理有 (\frac{\partial H}{\partial T})_p(\frac{\partial T}{\partial p})_H(\frac{\partial p}{\partial H})_T=-1 ,再重排变量有
(\frac{\partial H}{\partial p})_T=(\frac{\partial H}{\partial T})_p(\frac{\partial T}{\partial p})_H=-C_p\mu_{JT} (3-12) \mu_{JT} \mu_{JT}所以 dH=C_pdT-C_p\mu_{JT}dp
因为气体膨胀dp<0,等焓过程dH=0,所以有下图\mu_{JT} 为正时节流膨胀冷却,反之则变暖。
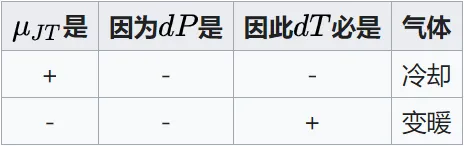
JT系数并不是一成不变的,对于真实气体,随着气体压强的升高,JT 系数由大变小,甚至出现负值。JT 系数从正值变到负值,必经过 JT 系数等于零的点。当 JT 系数为正值,即 \mu_{JT} >0,发生致冷效应;当 JT 系数为负值,即\mu_{JT} <0,发生致热效应;当 JT 系数为零,即\mu_{JT} =0,为理想气体,既不致冷,也不致热。可通过\mu_{JT} =0的点来判断\mu_{JT} 的正负,将一系列\mu_{JT} =0 的点连接起来就形成一条曲线,称为焦耳-汤姆逊反转曲线(JTIC),即通过此曲线时,焦耳-汤姆逊效应反转。通过 JTIC 很容易判断出实际气体的致冷区域和致热区域。在低压侧,即在 JTIC 内侧是致冷区域;在高压侧,即 JTIC 外侧是致热区域。
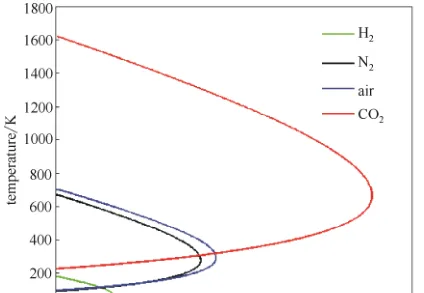
可以这样理解,在低压侧,当气体膨胀,分子 之间的平均距离上升。因为分子间吸引力,气体的位能 上升。因为这是等焓过程,系统的总能量守恒 ,所以位能上升必然会令动能 下降,故此温度下降;高压侧,当分子碰撞 ,动能暂时转成位能。由于分子之间的平均距离上升,每段时间的平均碰撞次数下降,位能下降,因此动能上升,温度上升。在制冷过程中我们需要的当然是低压侧的效应。
4、制冷剂循环
我们已经解锁了全部的物理化学过程前置,实现了从-1到0的改变,接下来我们正式开始介绍空调。
4.1四大装置
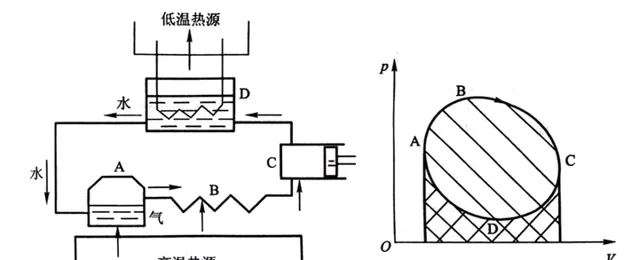
实现空调制冷循环的制冷剂五花八门,无论是压缩式还是吸收式,不管是非等温流还是解不出的复杂湍流,都必须遵循热力学第二定律,参照之前的卡诺热机循环,我们在这里给出卡诺冷机循环:
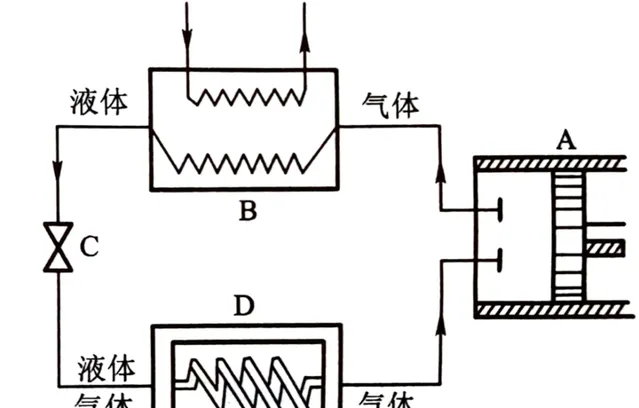
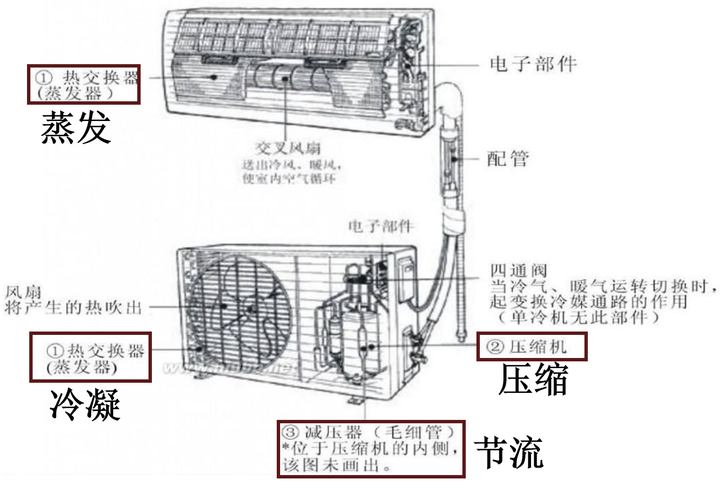
1)气态制冷工质被压缩机A压缩后成为 高温高压蒸汽 ;
2)压缩蒸汽进入冷凝器B中冷却后成为 中温高压 后释放汽化热(相变焓)成为 液体 ,释放Q1热量;
3)中温高压液体进入节流装置C进行等焓节流膨胀成为 低温低压湿蒸汽(气液混合态) ;
4)低温低压湿蒸汽进入蒸发器D中,吸收Q2热量,全部蒸发为 低温低压过热蒸汽 (仍比蒸发风低),随后进入下一循环。
这里由于外部做功,制冷效率算出来会大于1,因此这个值也称为制冷系数,制冷剂经过的ABCD四个装置是市面上绝大多数空调所必须具备的。其中压缩机A现在已经都是密闭式涡旋压缩机;冷凝器B其实就是一排排线圈缠绕管,配合冷凝风扇向室外散热;冷凝管出来后的液体去节流装置C前还有经历一遍干燥过滤,节流阀多为热力膨胀阀或电子膨胀阀;节流膨胀后的低温低压湿蒸汽经过蒸发器D,和冷凝器相同的线圈和风扇,只不过是向室内吹风,重新变回低温低压过热蒸汽。
ABC一般放空调外机,D一般放在空调内机。
为了更加准确计算真实制冷剂的效率,需要借助压焓图判断工质在各个机组的状态,这里仅做定性介绍。
压焓图曲线的含义可以用一点(临界点)、二线(饱和液体线、饱和蒸汽线)、三区(液相区、两相区、气相区)、五态(过冷液状态、饱和液状态、过热蒸汽状态、饱和蒸汽状态、湿蒸汽状态)和八线(等压线、等焓线、饱和液线、饱和蒸汽线、等干度线、等熵线、等比体积线、等温线)来概括。
这里可以参考空调压焓图
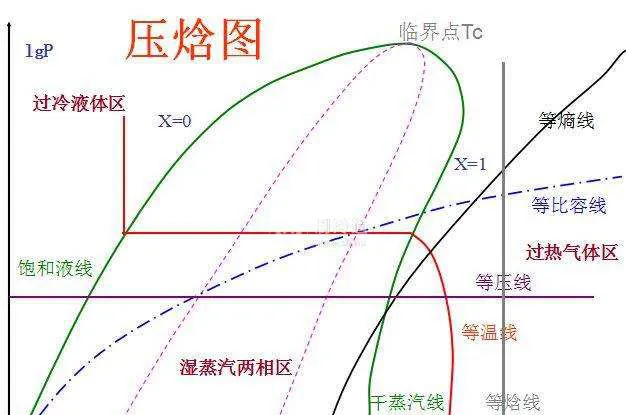
很抽象对不对,其实并不需要记忆多少概念,我们结合实际的循环来看,以R407C制冷剂为例。在单级压缩焓图中:A点对应的是11℃的过热蒸汽(焓h=412kJ/kg);压缩至B点55℃的高温高压蒸汽(焓h=432kJ/kg);冷凝器冷却后为中温高压液体,36℃达到饱和(焓h=245kJ/kg)C点31摄氏度达到过冷(焓h=238kJ/kg);节流膨胀降压过程等焓,D点温度降低至6℃的低温低压湿蒸汽;蒸发器蒸发后重新变成11℃的过热蒸汽(焓h=412kJ/kg)。

压缩焓图中,蒸发后的饱和蒸汽并不是达到饱和蒸汽线(干蒸汽线)就开始压缩,这个过热蒸汽是防止压缩机被液化击穿,一般为5℃;胀阀后,必须要在蒸发器内将液体变为气体,因此在节流膨胀前要进行过冷却过冷度一般为5℃。
过热度:吸入气体温度-蒸发温度过冷度:冷凝温度-膨胀阀前温度
4.2冷热模式
我们知道功可以自发转变为热量,但是这种转变太慢。我们把卡诺冷机反过来,交换一下制冷剂的循环顺序,使压缩机把压缩后的高温高压气体进入蒸发器,蒸发器本来就是向室内吹气,这样把高温制冷剂热量通过强迫热对流传递给室内,似乎2个装置就可以完成循环。但是,还记卡诺定理吗?这个温差简直就是能耗黑洞。而就现实来说,没有节流降压过程,蒸发散热后的液体更不可能被压缩,所以必须经过完整的卡诺循环。
我们按照相反过程推导:
1)气态制冷工质被压缩机A压缩后成为 高温高压蒸汽 ;
2)压缩蒸汽进入蒸发器D中冷却后成为 中温高压 后释放汽化热(相变焓)成为 液体 ,释放Q1热量;
3)中温高压液体进入节流装置C进行等焓节流膨胀成为 低温低压湿蒸汽(气液混合态) ;
4)低温低压湿蒸汽进入冷凝器B中,吸收Q2热量,全部蒸发为 低温低压过热蒸汽 (仍比蒸发风低),随后进入下一循环。
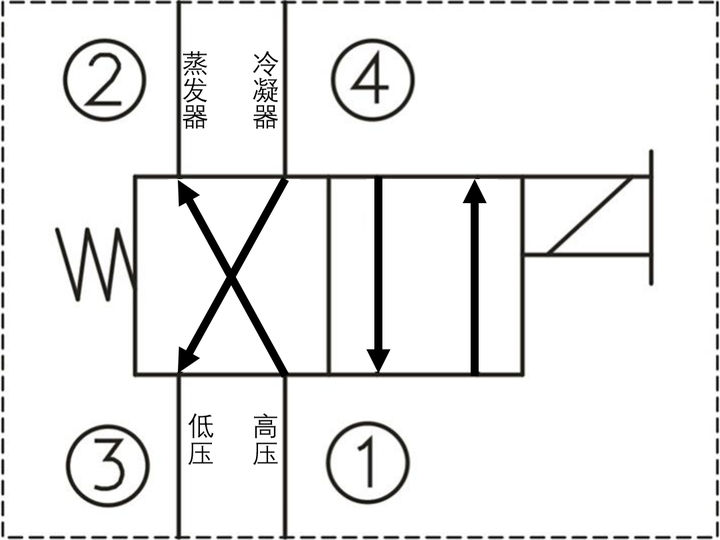
这实质上也是 从低温热源吸热,向高温热源放热 的冷机过程。为了实现冷热模式交替,需要切换制冷剂流经蒸发器和冷凝器的方向,这里我们可以直接使用一个二位四通阀。对于压缩机,我们不能弄错高压和低压的流向,必须时制冷剂总是从低压进高压出,同样对于膨胀阀和干燥器,我们也要设置一个二位四通阀,使得总是节流膨胀,这样一来,我们空调开启制冷模式时四通阀是一个位,开启制热模式时四通阀又是一个位。不过对于很多地方,空调制热时目标温差要远大于制冷时的目标温差,所以在具有制热模式的空调蒸发器风扇外增设了电热管,进一步改善制热效果。
后面的温度调节,电控方法之类的我觉得不是原理,更偏应用,就不展开了。
5、番外篇
基于节流膨胀的制冷已经被开发一百多年了,尽管这些年也诞生了很多非主流制冷方式,但空调依旧是比别的制冷方式节能。
5.1空气液化
在空调制冷剂循环中,我们都是用沸点比较高(室温能达到)的制冷剂作为例子,它们在经过冷凝器后就已经是液态,节流膨胀只是让其温度进一步降低,试想一下,我们如果我们不要蒸发过程了,只要控制温压在JT反转曲线内,是可以继续降温的,但是如果需要使用节流效应进行 等焓液化 ,我们需要看另一个图——温熵图。
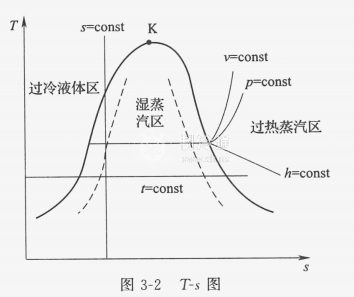
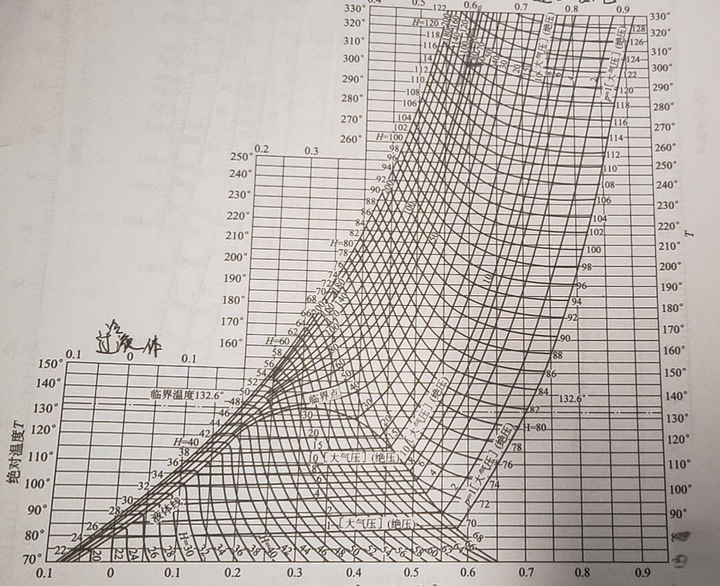
温熵图和之前提到的压焓图有点像,也分为过冷液体区、湿蒸汽区和过热蒸汽区,也有临界点,而且实际上用途更广泛。首先是 等温线 和 等熵线 ,它们就是和横纵坐标平行的线,如果用温熵图描述卡诺热机,我们就可以得到一个标准的矩形。 等压线 :在湿蒸汽区近乎与等温线重合;在过热蒸汽区为 左下至右上曲线 ;过冷液体区,等压线密集于饱和液体线附近,可近似以饱和液体线代替。 等焓线 :为 左上至右下曲线 ,湿蒸汽区坡度大,过热蒸汽区较平坦。此外还有等溶线、等干度线等。上面提到的液化实际上就是气态经等焓线进入气液两相区的过程。比如下面的空气温熵图中,我们在10MPa(100个大气压)下时,温度要低于169.4K才能沿等焓线液化。
目前液化空气的方法有林德(Linde)过程和克劳德(Claude)过程。林德过程也就是林德-汉普逊循环。原理如下,①通过压缩加热气体,以给予其参与循环所需的外部能量。②将气体浸入低温环境的方式将其冷却,使其失去一部分热量;③节流膨胀,现阶段气体达到整个过程的最低温度,将再度循环并被送回;④送回后的气体经换热器冷却下一阶段的返流气体;⑤回到阶段①开始下一循环。在这个简图中,似乎只有外界对系统做功,温度应该是上升,实际上冷凝是有另一套循环的,我们可以在温熵图中进一步深入。
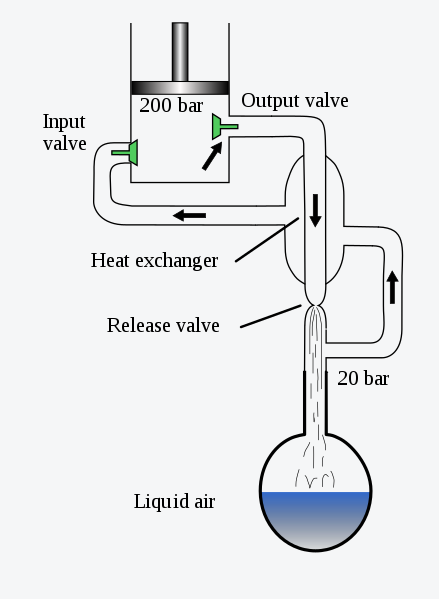
在林德循环中: 状态1 处于压强为p1的气体,经压缩机压缩至压强p2后等压冷却至 状态2 ,该气体经逆流换热器被分离返回后的气体进一步等压冷却至 状态3 ,再经节流效应等焓液化至湿蒸汽区的 状态4 ,在贮分离器中液化后 状态0 的液态会被分离器不断导出,未被液化的 状态5 气体被导出经过逆流换热器给下一波状态2气体冷却后再和状态1的气体一起被压缩。这个过程冷却和换热的液体都是随着循环进行温度越来越低的,因此可以将空气液化。
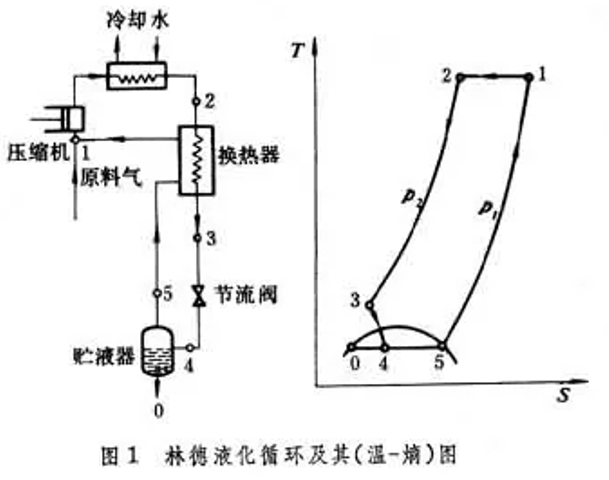
节流膨胀不对外做功,而绝热膨胀可对外做功,因此理论上可制取更低温度,但低温液化会造成损失,因此膨胀机必须与节流阀共同使用,为此克劳德循环增加了2个换热器和1个膨胀机。我们从状态3开始分析,其中的一部分气体沿3→8绝热膨胀至 状态8 ,另一部分经换热器2(状态4)、换热器3(状态5)、节流阀(状态6)后,液化后的状态0,未液化的状态7都与林德循环相同,状态7气体经逆流换热器3后与膨胀机出口状态8汇合,汇合后的气体经换热器1、2后进入压缩机进入下一个循环。
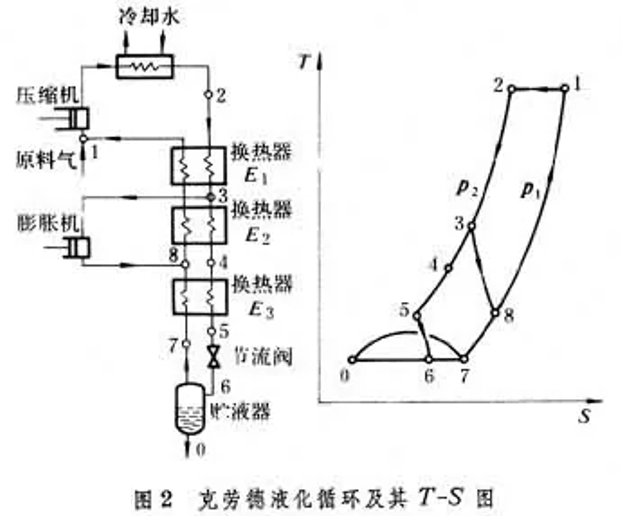
5.2半导体制冷
之前所有的降温过程都或多或少用上了JT效应或者膨胀做功,那么接下来我们看一点不一样的。
热电效应( 英语:Thermoelectric effect)是一个由温差产生电压的直接转换,且反之亦然。简单的放置一个热电装置,当他们的两端有温差时会产生一个电压,而当一个电压施加于其上,他也会产生一个温差。
1821年塞贝克发现将二种不同金属 各自的二端分别连接构成的回路,如果两种金属的两个结点处温度不同,就会在这样的线路内发生电流。这种现象称为 赛贝克效应 (Seebeck Effect)。
1834年珀尔帖 发现了与塞贝克效应 的相反效应,即当电流流经两个不同导体形成的接点时,接点处会产生放热和吸热现象,放热或吸热大小由电流的大小来决定。这就是 珀尔帖效应 (Peltier Effect)。
1854年威廉·汤姆森 将一根导线通恒定电流,由于导线有电阻而发热。再将这根带电的导线的某小局部加热;使它产生温度梯度 。这根导线就在原有发热的基础上,出现吸热或放热的现象。或者反过来,当一根金属棒的两端温度不同时,金属棒两端会形成电势差。这就是 汤姆森效应( Thomson effect)
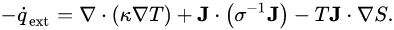
在只有金属导电的年代,这几个效应确实只能叫「热」电效应,但是在半导体时代,我们有更好的用途。根据塞贝克效应我们可以得到塞贝克系数的定义:当对材料施加温度梯度时,以及当材料达到电流密度 处处为零的稳定状态时,建立的电压。
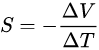
从物理上讲,塞贝克系数的大小和符号可以理解为材料中电流携带的每单位电荷的熵。它可能是正的或负的。对导体中独立移动的自由电荷载流子 ,塞贝克系数对于带负电的载流子(例如电子 )为负,对于带正电的载流子(例如电子空穴 )为正。
塞贝克效应通常主要由电荷载流子扩散的贡献决定,电荷载流子扩散往往会将电荷载流子推向材料的冷侧,直到建立补偿电压。因此,在p型半导体 , S 为正,在n型半导体 (仅具有负移动电荷,电子 )中, S 为负。然而,在大多数导体中,电荷载流子表现出类空穴和类电子行为,并且 S 的符号通常取决于它们中的哪一个占主导地位。
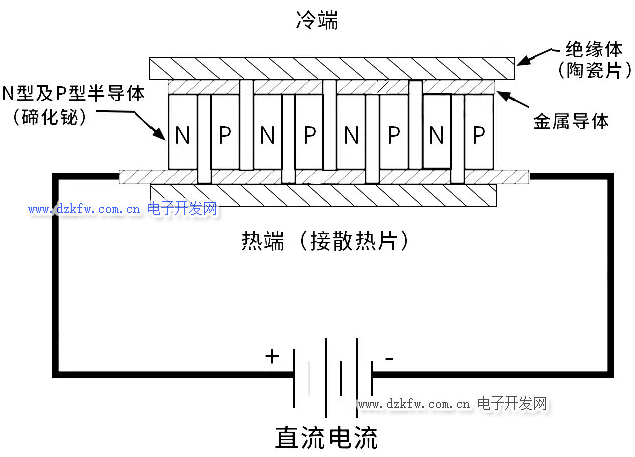
对于一般金属导体和N型半导体,都是电势高的地方为热端,电势低的地方为冷端,而P型半导体则相反。根据这个效应,我们将很多个这样的半导体联结成电偶对时,在这个电路中接通直流电流后,就能产生能量的转移,电流由N型元件流向P型元件的接头吸收热量,成为冷端;由P型元件流向N型元件的接头释放热量,成为热端。
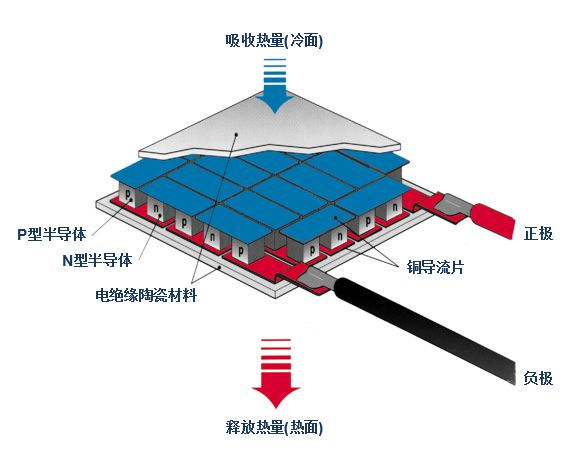
这样的元器件就是半导体制冷器(Thermoelectric cooler),不过若要使用它来制冷,得准备比它自身大得多的风扇,而且这个只能用于热传导接触制冷,因为实在是带不起风扇吹出的制冷量。

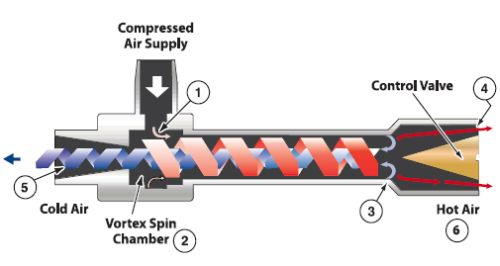
5.3涡流管制冷
这里参考涡流管到底怎么制冷的
涡流管制冷是一种借助涡流管的作用使高速气流产生漩涡分离出冷、热两股气流,利用冷气流而获得制冷方法。涡流管其实和上面的TEC很像,就是一端制冷另一端制热,只不过对于民用制冷来说使用条件更加严格,需要3-10bar的进气压力,通常为7bar,这导致没有压缩空气的地方必须要带一个空压机,噪音就太大了。
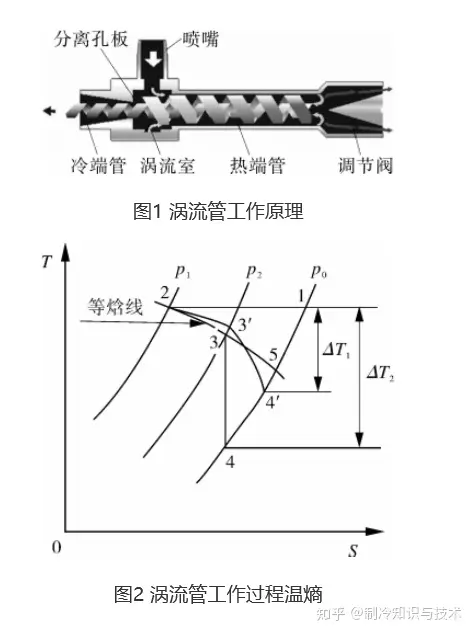
我们再来看能耗,也就是涡流管的温熵图,围成面积对应量纲为能量。
图中p0、p1、p2分别为环境大气压、喷嘴出口压力、空压机出口压力,ΔT1为实际温降,ΔT2为理论最大温降。1-2-3-4-1为理想涡流管的制冷循环,其面积为理想涡流管制冷量,环境空气进入空气压缩机等温压缩,后经喷嘴的节流过程,进入涡流管绝热膨胀,最终排出冷热端管。
图中2-3'为实际喷嘴节流降温过程,过程中摩擦等损失使焓值增加,3'-4'为实际涡流室中气体膨胀降温过程,其膨胀效率介于绝热膨胀与绝热放气之间,焓减小一部分转化为气体的推动功,因而其制冷效率总是比理想节流的等焓过程高。1-2-3'-4'-1为实际涡流管制冷循环,其面积为实际涡流管制冷量。2-5为等焓线,1-2-5过程为单一利用空气压缩机出口气体进行节流制冷循环的制冷量。从图可以发现理想及实际涡流管总的制冷量总是比单一运用节流效应制冷的制冷高。
但是,实际上空调并不需要涡流管如此猛烈的温降,而且涡流管不像空调把空气循环和制冷工质循环分开,这导致在空气净化上还是得额外走一路,高温气体回收困难,综合成本下来还是空调最划算。