看了一圈答案,有很多游戏机制、心理学角度解答问题的,不少都回答得很有启发性,但遗憾的是,唯独没有从纯数学角度解答这个问题的。
而从纯数学角度讲,这个问题本质上就是在讲「天花板函数的性质」。
在 高票答案 中,作者提到了「最大众化」的理解:
10% 闪避率 = 受到伤害时有 10% 的概率完全规避这次伤害;10% 减伤 = 受到的所有伤害降低 10%;
—— 事实上,这也是「唯一」准确的理解。
在实际游戏中,「10% 闪避率」和「10% 减伤」可能会存在一些因为暴露游戏策划数学水平不足的歧义理解,比如:
我原本闪避率是 20%,现在又堆了「10% 闪避率」,因此我现在的闪避率是 30%。对吗?
不对。
正确的说法是:
我原本闪避率是 20%,现在又堆了「10 % 闪避率」,因此我现在的闪避率是 22%;我原本闪避率是 20%,现在又堆了「10 pp 闪避率」,因此我现在的闪避率是 30%;
「百分比」(%)是两个数「相除」得到的结果;而两个「百分比」(%)相减,结果应表示为「百分点」(pp)。
因此,在数学表达无误的情况下, 原问题的理解是唯一的,并不存在歧义。
那么在这个定义下,理想模型下,相同初始条件时,两个属性价值相同吗?
并不相同。
高票答案提出了 EHP(有效生命)的概念,然而这个模型存在一些纰漏,就是它
忽略了边界条件
。
举个简单的例子:你有 100 点血,对手砍你一刀能打 80 滴血,你能抗几刀?
按照 EHP 的概念,你能抗 1.25 刀;
实际上呢?2 刀。
这个误差也太大了。
因此,我们需要引入我们熟悉的「天花板函数」:
ceil(x):返回不小于 x 最小整数。假设在正常情况下,对方砍你一刀能砍掉你血量的占比为 k;
那么:
对于 「10% 减伤」,我们能承受的刀数为:ceil(1/k/0.9);这个值是稳定的。
而对于「10% 闪避」,我们能承受的刀数和运气相关,似乎涉及到一些风险偏好问题,但学过概率就知道,其总挨刀数的期望是固定的,即 ceil(1/k)/0.9。
那么, ceil(1/k/0.9) 和 ceil(1/k)/0.9 哪个大?
请看下图:
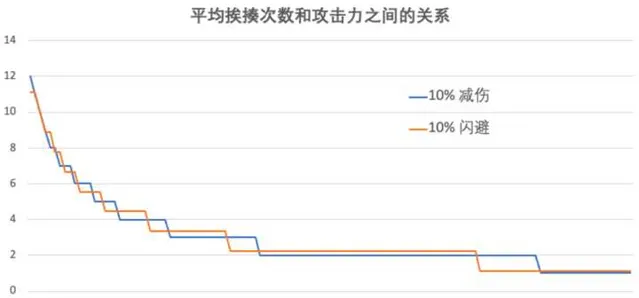
这两个函数并不是一致的,而是「纠缠不清」的。
事实上我们发现,两个函数孰大孰小,其根本在于 ceil 函数对数值本身的扩大作用;
而从图中可以明显看到:
当然,不同的游戏机制,会导致结果变得完全不同:
—— 如果对手有「连击加伤」,那么闪避会提升连击中断的可能性,其作用就会明显变大;
—— 如果对手有「击中附加负面效果」,比如中毒之类的,显然闪避的效果更好;
—— 如果自己有「闪避反击」,显然闪避更有用;
—— 如果自己有「受伤反击」,并且反击强度和受到伤害的程度无关,减伤会让你的技能依旧发动,那么减伤的作用就会更好。
由此可见,从游戏机制讲,由于连击技、附加效果、闪避反击的广泛存在, 受伤反击的技能偏少(有相当一部分还是和受伤血量挂钩的),在大部分情况下,「闪避率」是更好用的技能——尤其是在考虑人有赌性的情况下。











