奥利给不等式 就是:

哈哈哈哈,开个玩笑~
其实,这是个谐音,「奥利给不等式」指的是「ALG不等式」(Arithmetic-Logarithmic-Geometric mean inequalities),中文又称「对数均值不等式」 [1] 。
定义是:
\forall a,b>0\cap a\ne b. \Rightarrow\frac{a+b}{2}>\frac{b-a}{\ln b - \ln a}>\sqrt{ab}\tag{1}
即对于任意两个非负且互不相等的数 a 和 b ,两者的 算术平均数(Arithmetic mean) \frac{a+b}{2} 大于 对数平均数(Logarithmic mean) \frac{b-a}{\ln b - \ln a} 大于 几何平均数(Geometric mean) \sqrt{ab} 。
对应的证明方法有很多,我找到了一个由 Roger B. Nelsen 教授给出的图解证明法 [2] ,这也是我所见过的最为直观简洁的奥利给不等式证明方法,但是由于其原文中的公式有些错误,所以这里重新写一遍。
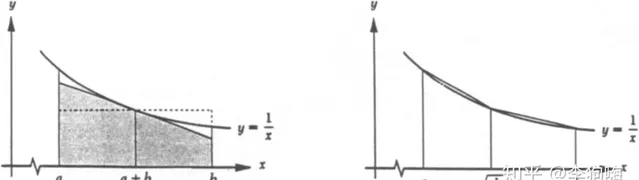
思路其实就是对比函数 y=\frac{1}{x} 在区间 (a,b) 所围的面积与一个通过「内切」(左边图)形成的梯形面积与两个通过「外接」(右边图)形成的梯形面积,进而得到不等式关系。
很显然,两种情况下,函数 y=\frac{1}{x} 在区间 (a,b) 所围的面积都为:
\int_{a}^{b}\frac{1}{x}dx=\ln x|_{a}^{b}=\ln b - \ln a \tag{2}
对于左边的图,根据积分所得面积与梯形面积的关系有:
(注意这里的梯形可以看做是长为 b-a ,高为 \frac{2}{a+b} 的矩形)
\ln b-\ln a>\frac{2}{a+b}(b-a)\tag{3}
\frac{a+b}{2}>\frac{b-a}{\ln b -\ln a}\tag{4}
对于右边的图,根据积分所得面积与两个梯形面积和的关系有:
(开始吟唱:梯形的面积是上底加下底的和乘高除二!)
\ln b -\ln a<\frac{1}{2}\left(\frac{1}{a}+\frac{1}{\sqrt{ab}}\right)\left(\sqrt{ab}-a\right)+\frac{1}{2}\left(\frac{1}{b}+\frac{1}{\sqrt{ab}}\right)\left(b-\sqrt{ab}\right)\\=\frac{ab-a^2}{2a\sqrt{ab}}+\frac{b^2-ab}{2b\sqrt{ab}}=\frac{b-a}{\sqrt{ab}}\tag{5}
\sqrt{ab}<\frac{b-a}{\ln b - \ln a}\tag{6}
综上有:
b>a>0\Rightarrow\frac{a+b}{2}>\frac{b-a}{\ln b - \ln a}>\sqrt{ab}\tag{7}
而对于题主的问题,关于 \ln x 与 \frac{2x-2}{x+1} 的关系就很好比较了。
由奥利给不等式有:
\frac{x+y}{2}>\frac{x-y}{\ln x - \ln y}\tag{8}
现在只需要令 y=1 则有:
\frac{x+1}{2}>\frac{x-1}{\ln x - \ln 1}\tag{9}
所以当 x>1 时,有:
\ln x>\frac{2x-2}{x+1}\tag{10}
当 0<x<1 时,有:
\ln x<\frac{2x-2}{x+1}\tag{11}
当 x=1 时,有:
\ln x=\frac{2x-2}{x+1}\tag{12}
参考
- ^ Logarithmic mean https://en.wikipedia.org/wiki/Logarithmic_mean
- ^ Nelsen, Roger B. "Proof without Words: The Arithmetic-Logarithmic-Geometric Mean Inequality." Mathematics Magazine 68, no. 4 (1995): 305. doi:10.2307/2690586.











