这种数学问题下怎么可以没有MATLAB?
其他答主都做的非常好, 但是没人用MATLAB做. 那我们就用MATLAB做一遍呀.
\pi 中 0123456789 这 10 个数字是否出现的概率一样, 即, \pi 中数字是否是均匀分布的, 目前数学界还没有证明. 符合这种条件的数叫做正规数, 但是目前并没有在数学上证明 \pi 是正规数. 不过, 题主既然要数据支撑, 我们倒是可以探讨有限位下 10 个数字出现的概率是否大致相等.
我们用一下MATLAB呀.
先写个万年不变的起手式.
clear
然后...好像没什么好说的, 代码比较简单.
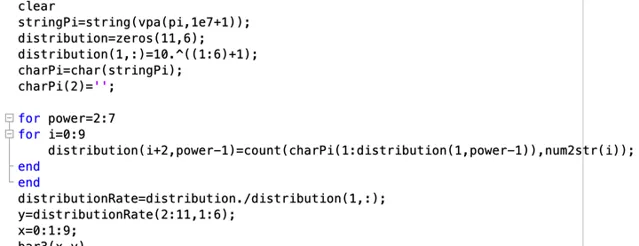
大概解释一下, 我取了6个 \pi 的位数, 分别是 100,1000,10000,100000,1000000,10000000 ,也就是一百, 一千, 一万, 十万, 百万, 千万位.
在获取到对应位数的 \pi 的至之后, 转换成string格式, 再转换成char格式.(MATLAB sym格式不能直接转换成char).
转换成char格式之后, 再用两个循环分别统计不同 \pi 位数下各个数字出现的次数(频数).
之后再将频数转变成频率, 最后在对每个数字对应的频率和位数进行作图.
clear
stringPi
=
string
(
vpa
(
pi
,
1e7
+
1
));
distribution
=
zeros
(
11
,
6
);
distribution
(
1
,:)=
10.
^((
1
:
6
)
+
1
);
charPi
=
char
(
stringPi
);
charPi
(
2
)=
''
;
for
power
=
2
:
7
for
i
=
0
:
9
distribution
(
i
+
2
,
power
-
1
)=
count
(
charPi
(
1
:
distribution
(
1
,
power
-
1
)),
num2str
(
i
));
end
end
distributionRate
=
distribution
./
distribution
(
1
,:);
y
=
distributionRate
(
2
:
11
,
1
:
6
);
x
=
0
:
1
:
9
;
bar3
(
x
,
y
)
set
(
gca
,
'XTickLabel'
,{
'100'
,
'1000'
,
'10000'
,
'100000'
,
'1000000'
,
'10000000'
});
xlabel
(
'重复次数'
);
ylabel
(
'数字'
);
zlabel
(
'频率'
);
OK了, 我们看一下结果?
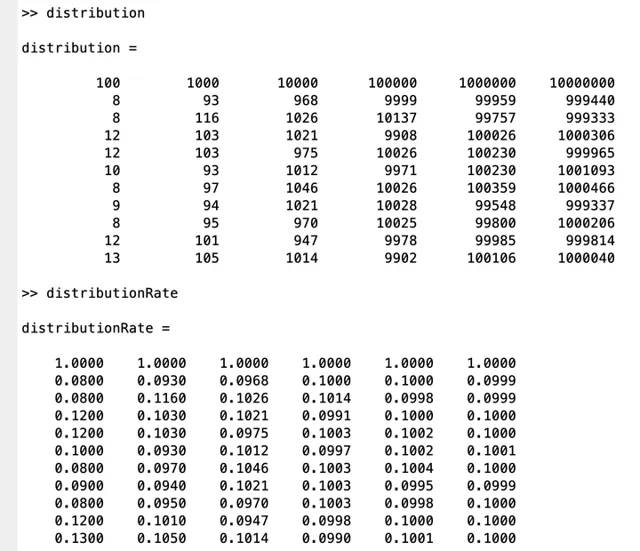
可以直观地感受到, \pi 的位数越多, 各个数字的频率就越收敛于 \frac{1}{10} .
那能不能更直观一点呢? 既然是用MATLAB做, 怎么少得了画图呢?
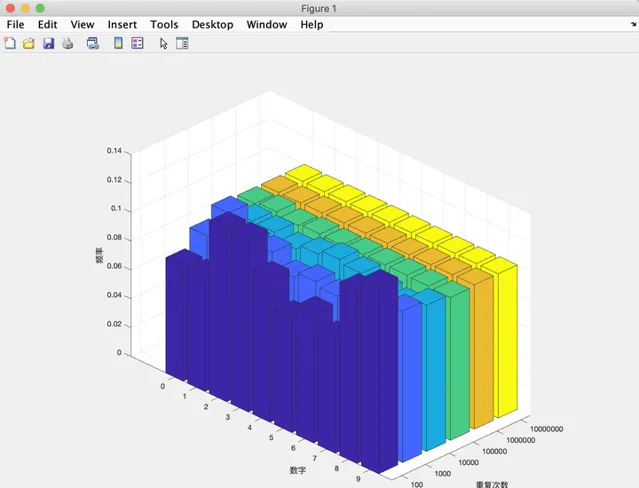
用bar3(x,y)函数将数据画成3位柱形图, 这下可以完全直观地看到, 重复次数, 也就是位数, 越大, 每个数字的频率越靠近 \frac{1}{10} .
所以可以这样回答问题, 在 \pi 的小数点后 10000000 位, 各个数字出现的概率是几乎一样的.








