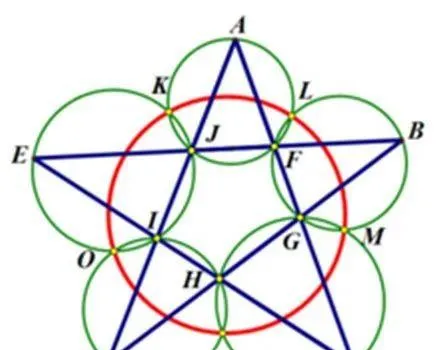
远在2000年12月20日,江泽民主席出席澳门回归祖国一周年庆典活动期间,在参观濠江中学时向该校师生出了一道求证「五点共圆」的平面几何题:「假设:任意一个星形,五个三角形,外接圆交于五点。求证:这五点共圆。」
江主席说:「我也当过中学教师,所以我对教师感到特别亲切。中学教学,要教好语文、历史、地理,数学也应该重视。」「我把这道题出给濠江中学,是要说明:一个人总要有钻研精神。」
香港科技大学数学系副教授李健贤说,三角几何能提供逻辑及观察力的训练,可锻炼分析能力。不过,香港的数学教育注重运算,较少要求学生去处理这类几何难题。香港只有少数大学生能解答江主席出的这道几何题。香港喇沙中学的一名会考十优生陈贵祥表示,老师曾讲授过这道考题的基本理论,但他并未做过与这道考题相关的习作。
据说,数学大师丘成桐也用了半小时才悟出此难题答案。
2000年12月28日,澳门濠江中学师生给江主席寄出了答案。两天后,江主席请澳门特区行政长官何厚铧转交了给濠江中学师生的回信。
已知与求证
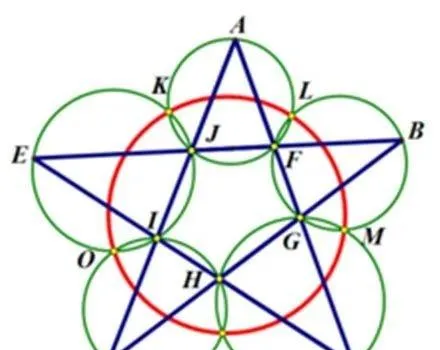
如图,在任意五角星AJEIDHCGBF中,△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圆顺次相交的交点分别是K、O、N、M、L。
求证:K、O、N、M、L五点共圆。
证明思路分析
多点共圆问题一般常见的是四点共圆,因为3点确定一个圆,4个点则是这个共圆结构需要探讨的最简形式。而一般的多点共圆问题也会转化为多个四点共圆问题来解,即如果1234共圆,其中的3个点的组合(不妨设为123)和5共圆,那么它们都是共的三角形123的外接圆,4和5都在三角形123的外接圆上,故5点共圆。
这里根据五角星的射影几何性质的C5对称性,KLMNO五点中任意取4点的方法也是对称的,即连续4点。且证明其共圆的方法一定和其他连续4点相同,故问题转化为证明LMNO四点共圆(取剔除第一个字母K的代表元素)。
而证明四点共圆的一般思路,总的来说就是各种圆上边和角相关性质定理的逆定理,大体上恰好定理的描述涉及到圆上的4个点即可。而这些定理的源头都来源于同弧所对圆周角相等这样的优雅性质(再往前就是三角形外角等于不相邻内角和和因为圆的定义得到的以圆心角为顶点的一众等腰三角形了)。由此,才有了内蝴蝶的两个三角形翅膀的相似和相交弦定理。
当两个点不在某线段同一侧时,圆周角相等变成了内对角互补或外角等于内对角。这才有了顶点在圆外的相似三角形以及切割线定理,割线定理。
都组合起来,才有了托勒密定理,西姆松定理等。
所以本质上还是因共线构造的角和关系,因半径相等构造的等边三角形的底角相等为一切性质的源头。在没有直接的边相关的条件和结论证据时,我们优先考虑角。
如果以KN为弦,L和M为同侧顶点,证明圆周角相等,这并不是一个好思路,因为哪怕把∠KLN用相交弦LF拆开成两个角,依然有∠FLN对着一个不知道圆上交点在哪的弧,无法进行圆上各种转换。
LM为弦,K和N为同侧顶点是类似的问题。
那就换一对不同侧的,LN为弦,K和M为不同侧顶点,或者对换一下,都对称等价。总之把思路变成证明内对角互补或等价的外角等于内对角,是明确的思路。
此时∠LMN被相交弦拆为∠LMG和∠GMN,这两个角是对称的。反复用圆周上角的关系有:∠LMG = ∠LFA = ∠LKA,但如果两侧都用同样的转化,得不到什么。
但另一侧还有∠GMN = ∠GCN。两边一比对,发现待证明的成了∠AKN + ∠ACN = 180°的ACNK四点共圆问题。
但这依然不好证。问题依然在于,无论用哪条作参考弦,都存在不知道连出来的角和圆的交点有什么性质。
如果说要证明5点共圆很容易转化为4点的组合,那要证明4点共圆,想到要转化为两个5点,实在是太考验几何感觉了。
这也是平面几何没啥实用性,但最迷人的数学魅力。
继续看有没有一些角的相等转化,全靠圆上四点结构带来的角相等与互补关系:
∠ACN = ∠NHD = ∠NID,这就能得到ACNI四点共圆了,而这里只有I不是ACNK中的点。
但它竟然是这个结构中的一个对称不动点,也就是轻易的也有ACKI四点共圆。
于是得出ACNK四点共圆,原命题得证。
以上是我的思路分析,删减一下就是分析法解答了,正向的证明也参考如下。
证明:
连接CN、HN、KN、IN、MN、MG、ML、LF、LK、KA
∵∠ACN+∠AIN=∠NHD+∠AIN=∠NID+∠AIN=180° ∴A、I、N、C四点共圆
同理A、K、I、C四点共圆从而A、C、N、K四点共圆
∴∠GMN=∠GCN=∠ACN=180°-∠AKN又∠LMG=180°-∠LFG=∠LFA=∠LKA
∴∠LMN=∠LMG+∠GMN=∠LKA+(180°-∠AKN)
∴∠LMN+∠LKN=∠LKA+(180°-∠AKN)+∠LKN=180° 故K、L、M、N四点共圆
同理可证O、L、M、N四点共圆
∴K、O、N、M、L五点共圆
证毕。
谨以此文,聊表敬意。











