为了稍微系统一点地回答这个问题,也为了整理一下关于四元数的知识,这篇回答分为七个(不均等的)部分:复数与旋转、四元数的定义、四元数的性质、等距同构、虚四元数的乘积、四元数的共轭作用、共轭作用的效果。
开始了!
一、复数与旋转
在说四元数与旋转的关系之前,我们先回顾一下复数与旋转的关系:
每一个\mathbb{R}^{2} (关于原点)的旋转都可以用一个复数z_{\theta}=\cos\theta+i\sin\theta 来表示。这是因为,对于每一个点(x,y)=x+iy 来说:
z_{\theta}(x+iy)=(\cos\theta+i\sin\theta)(x+iy)=x\cos\theta-y\sin\theta+i(x\sin\theta+y\cos\theta)
所以z_{\theta} 把(x,y) 移到了(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta) 的位置,也就是旋转了\theta .
我们还可以把这个过程写成矩阵形式:
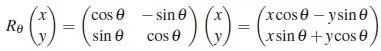
为了更好地看出复数与矩阵的联系,我们可以把矩阵写成这样的形式:
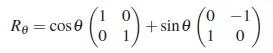
其中,

(顺带说一句,Bourbaki给法国中学生写的课本中,虚数就是直接这么定义的。)
于是,我们可以把每个复数都表示成矩阵的形式:
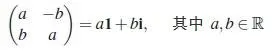
当我们把复数与矩阵结合起来的时候,我们就多了一种描述『和』与『积』等运算的角度。
二、四元数的定义
对于四元数来说,这种『矩阵表示』的方法同样适用。
每一个四元数q 对应了一个矩阵:
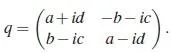
(这并不是四元数与矩阵的唯一对应方法,但这种方法是复数与矩阵对应的推广。)
【能不写矩阵形式吗?】
好吧,把四元数写成更喜闻乐见的形式就是这样的:
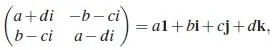
其中,
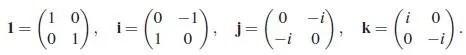
所以四元数就是在复数的基础上又加了\mathrm{j,k} ,并且同样地\mathrm{j}^2=\mathrm{k}^2=-1 ,此外还有运算法则:
\mathrm{ij=k},~\mathrm{jk=i},~\mathrm{ki=j}
\mathrm{ji=-k},~\mathrm{kj=-i},~\mathrm{ik=-j}
这些可以通过矩阵乘法来验证。(注意,四元数并不满足乘法交换律!)
我们把四元数空间记作\mathbb{H} ,以纪念其发现者Hamilton。
三、四元数的性质
四元数的很多性质与复数类似,比如:
每一个非零的四元数q 都有逆q^{-1} ,也就是其对应矩阵的逆矩阵。并且有:
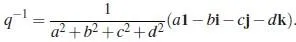
每个四元数q 都有与其共轭的四元数\bar{q} =a1-b\mathrm{i}-c\mathrm{j}-d\mathrm{k} ,并且q\bar{q}=|q|^2 . 其中,q 与\bar{q} 对应的矩阵则是共轭转置的关系。
定义|q|^{2}=\det q=a^{2}+b^{2}+c^{2}+d^{2} ,所以|q| 就是(a,b,c,d)\in \mathbb{R}^{4} 到原点的距离。
正如单位长度的复数对应了圆(一维球面\mathbb{S}^{1} )一样,单位长度的四元数满足a^2+b^2+c^2+d^2=1 ,对应了三维球面\mathbb{S}^{3} .
由于任意两个单位长度的四元数的乘积仍然是单位长度,所以\mathbb{S}^{3} 对乘法是封闭的。(实际上,\mathbb{S}^{3} 在四元数乘法下是一个群。)
四、等距同构
我们现在回过头再看复数与旋转的关系:
对于单位长度的复数u 来说,我们压根不需要计算三角函数就可以知道它对应了旋转。对于任意v,w 两个复数,我们考虑它们的距离在乘u 前后的变化:
|uv-uw|=|u(v-w)|=|u||v-w|=|v-w|
可以看出,它们的距离没有发生变化。用一个看起来高大上的术语来说,『乘u 』是一个『等距同构』。
同样地,我们我们可以用这种方法证明:乘上一个单位长度的四元数也是\mathbb{R}^4 中的等距同构。
五、虚四元数的乘积
四元数对应了四维空间,而我们要研究的是三维空间的旋转,所以我们把目光限定在四元数的一个子空间:『虚四元数』。
虚四元数就是实部为零的四元数,也就是形如p=b\mathrm{i}+c\mathrm{j}+d\mathrm{k} 的四元数。虚四元数构成了三维的空间,我们把它记作\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} .
显然,\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中任意两个元素的和还是在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中;然而当我们做乘法的时候,问题就出现了:
如果u=u_1\mathrm{i}+u_2\mathrm{j}+u_3\mathrm{k},~v=v_1\mathrm{i}+v_2\mathrm{j}+v_3\mathrm{k} ,那么它们的乘积是:
uv=-(u_1v_1+u_2v_2+u_3v_3)
~~~~+(u_2v_3-u_3v_2)\mathrm{i}-(u_1v_3-u_3v_1)\mathrm{j}+(u_1v_2-u_2v_1)\mathrm{k}
或者写成
uv=-u\cdot v+u\times v
由于u\cdot v 是实数,所以只有当u 与v 垂直时,uv 才在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中。
同时,注意到如果u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的单位向量,那么u^2=-u\cdot u=-|u|^2=-1 .
六、四元数的共轭作用
现在我们试着用四元数表示三维空间\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的旋转。
与复数一样,对于一个单位长度的四元数t ,我们也可以把它写成实部与虚部的和:
t=\cos\theta+u\sin\theta , 其中u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的单位向量。
我们希望把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 作为我们旋转的空间,然而我们之前已经发现,对于q\in \mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 来说,qt 可能不在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之中。这怎么办呢?
答案是:共轭——t^{-1}qt 一定在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之中。
为什么呢?首先我们注意到t^{-1}=\bar{t}/|t|^2=\cos\theta-u\sin\theta ,所以t^{-1} 存在。于是,在\mathbb{H} 中,乘t 与乘t^{-1} 都是\mathbb{H} 上的双射(因为可逆),所以q\rightarrow t^{-1}qt (称为t 的共轭作用)也是\mathbb{H} 上的双射。
由于对于任意实(四元)数r 都有t^{-1}rt=r ,即t 的共轭作用把\mathbb{R} 映到其自身,于是也会把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 映到自身。也就是说,t 的共轭作用是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 上的双射,这就解决了之前『qt 乘积会跑到\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之外』的问题。
好的,接下来我们可以具体来考察t 的共轭作用在三维空间\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的效果了。
七、共轭作用的效果
我们想要证明的是,给定t=\cos\theta+u\sin\theta ,其中u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的单位向量,那么t 的共轭作用将把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 绕着u 所在的轴\mathbb{R}u 旋转2\theta .
证明分两步,首先我们证明\mathbb{R}u 是旋转轴。这也就意味着,我们要证明u 的所有实数倍的向量在t 的共轭作用下保持原位:
t^{-1}ut=(\cos\theta-u\sin\theta)u(\cos\theta+u\sin\theta)
=(u\cos\theta-u^2\sin\theta)(\cos\theta+u\sin\theta)
=(u\cos\theta+\sin\theta)(\cos\theta+u\sin\theta) (因为u^2=-1 )
=u(\cos^2\theta+\sin^2\theta)+\sin\theta\cos\theta+u^2\sin\theta\cos\theta
=u (因为u^2=-1 )
接下来,我们在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中选取垂直于u 的单位向量v ,令w=u\times v . 于是,\left\{ u,v,w \right\} 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 的一组规范正交基。
为了证明确实旋转了2\theta ,我们只需要证明t^{-1}vt=v\cos2\theta-w\sin2\theta 以及t^{-1}wt=v\sin2\theta+w\cos2\theta 就好了。两者证明类似,这里只证明前者:
t^{-1}vt=(\cos\theta-u\sin\theta)v(\cos\theta+u\sin\theta)
=(v\cos\theta-uv\sin\theta)(\cos\theta+u\sin\theta)
=v\cos^2\theta-uv\sin\theta\cos\theta+vu\sin\theta\cos\theta-uvu\sin^2\theta
=v\cos^2\theta-2uv\sin\theta\cos\theta+u^2v\sin^2\theta (因为vu=-uv )
=v(\cos^2\theta-\sin^2\theta)-2w\sin\theta\cos\theta (因为u^2=-1,~uv=w )
=v\cos2\theta-w\sin2\theta
证明完毕!
于是,对于\mathbb{R}^3 中每一个旋转,给定旋转轴u 以及旋转角\alpha ,都有一个单位长度的四元数t=\cos(\alpha/2)+u\sin(\alpha/2) 的共轭作用与之对应。
此外,注意到两个旋转的叠加仍然是一个旋转,因为t_{2}^{-1}(t_{1}^{-1}qt_1)t_2=(t_{2}^{-1}t_{1}^{-1})q(t_1t_2)=t^{-1}qt ;以及,旋转的逆也是一个旋转。
同时,由于(-t)^{-1}s(-t)=t^{-1}st ,于是-t 对应了同一个旋转,所以这是一个『二对一』的对应关系,也就是其他答主所说的『从Spin群到SO群的二重覆盖映射』。
那么就这样=w=
参考资料:

(译为【天真的谎言理论】或【朴素李理论】)











