关于一光年的旅程,有这样一种观点,光并不需要一年时间来完成这段旅程。实际上,光的传播并不耗费任何时间,无论距离是一光年还是整个可观测宇宙的宽度(约930亿光年)。光是宇宙中时间与空间的界限,因此在这一情境下,时间的概念不再适用。

我们常说的「光年是光走一年所经过的距离」,其中的「一年」实际上是基于地球上的人类对于时间的感知,而非光自身的时间。
只有在物体速度尚未达到光速时,物体的时间流逝才会出现减慢的现象,这正是狭义相对论中的时间膨胀效应。如果物体的速度等同于光速,那么该物体便成为光的一部分。由于光不经历时间,因此处于光速的物质并不是时间流逝缓慢,而是时间根本就不存在。然而,问题在于,具有非零静质量的物质理论上无法达到光速。狭义相对论的质量与速度关系公式清楚地揭示了这一点:
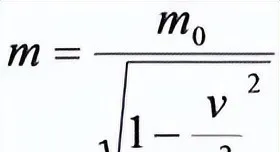
(其中m为物体的运动质量,m0为物体的静质量,Ⅴ为物体的运动速度,c为光速),当V→c时,分母趋于0,则趋于无穷大,换言之,当物体速度接近光速,其质量将趋于无穷大。如果宇宙的总能量有限,那么这些能量不足以推动这样一个具有非零静质量的物体达到光速。这个结论基于一个假设,即光速在所有参考系中都是恒定的。光速恒定这一观点来源于麦克斯韦方程组的推论,并被多次实验和观测所证实。例如,在大型粒子加速器中,无论我们为粒子提供多少能量,粒子的速度始终无法达到光速。这就是光速极限的原理。
让我们回到最初的话题,考虑一个人在光速飞船中度过一年与地球上的一年有什么不同。如前所述,飞船不可能达到光速,如果飞船速度等同于光速,飞船中的人同样以光速移动,他们与飞船都成为光的一部分,不再经历时间,因此不存在「一年」的概念。设想飞船达到光速,而人相对于光速静止,继续日常活动,这种想法是错误的。
当人乘坐亚光速飞船时,时间的概念才重新变得有意义。在这种情况下,飞船中的一年与地球上的一年在体验上是相同的,但在时间的相对性以及同时性的相对性上存在差异。

以人前往距离地球约4光年的半人马座比邻星为例,飞船以接近光速的速度飞行,对地球上的观察者来说,飞船需要4年多时间穿越4光年的距离;但对飞船上的人来说,他们所用的时间将少于4年,因为在他们看来,地球和目的地都在相对移动。
这里涉及的一个重要问题是,虽然地球上的观察者发现飞船经过了4年的旅程,但飞船上的时钟相对于观察者来说,其时间流逝速度变慢了。飞船上的宇航员会观察到,他们的动作和飞船的长度都变慢了。与此同时,宇航员们会觉得自己的时间并没有减慢,相反,他们会发现地球的时间流逝速度变慢了。这意味着,虽然地球上的观察者觉得亚光速飞船上的人度过了缓慢的时间,但从飞船上的角度看,地球上的时间流逝得更慢。这就是所谓的「时间佯谬」或「双生子佯谬」。

如果飞船持续进行匀速直线运动,不返回地球,那么飞船上的「一年」与地球上的「一年」是等价的。然而,一旦飞船减速并返回地球,飞船上的时间相对于地球的时间就显得膨胀了,过得更加缓慢。这是因为通过加速和减速,飞船实际上已经改变了其所在的参考系,从而真正改变了时间。飞船上度过的「一年」在地球上可能会对应多个年头。于是,像双胞胎中的一个成为宇航员,当他返回地球时,会比留在地球上的兄弟更加年轻。飞船速度越接近光速,这种时间膨胀效应就越显著。具体可以用以下公式表示:
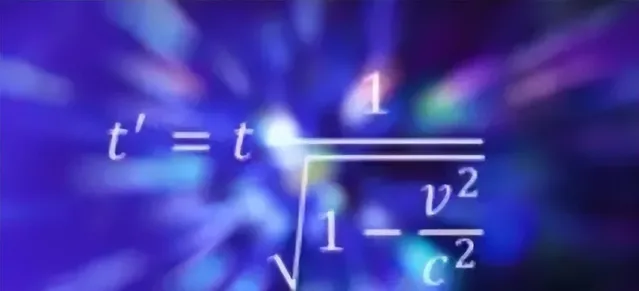
其中t′表示地球上的时间,t表示飞船上的时间,V为飞船的速度,c为光速。从公式可以看出,当V趋近于c时,分母趋近于0,t′趋近于正无穷大,这意味着飞船速度越接近光速,飞船上哪怕只度过很短的时间,地球上却要度过相当长的时间。例如,假设飞船上的一年,当V=0.99c时,地球上度过的时间t′约等于7.089年。当V=0.999999c时,地球上度过的时间t′约等于707年。感兴趣的读者可以进一步计算。上述公式反过来使用,即用t′来计算t,则可以计算出飞船以接近光速的速度飞行时,地球上度过的时间。
无论飞船和地球之间的时间差有多大,不同参考系中的观察者对于时间的主观感受(即意识时间)是相同的,而对于时间的实际流逝速度(物质时间)则无法直接察觉!!











