一、同一物体的各个部分,速度可以不同
首先,需要向题主明确强调的是:对于同一物体,各部分的速度本身就可以不同。
其实,这是一个很明显的常识。
物体只有在不发生自身转动的情况下,各部分的速度(大小 和 方向)完全相同。譬如:做匀加速直线运动的小木块、月球围绕地球公转,都属于这种情况。
反之,如果物体本身发生转动,那么各部分的速度都不相同。否则,物体就无法实现转动。 (划重点)
一个最经典的例子就是:同一个圆盘上的两个点,离转轴越远的点,旋转半径越大,从而线速度也越大。
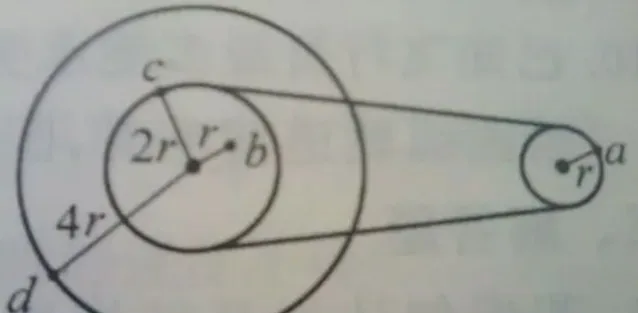
如图所示,对左边的大转轮,由于 b、c、d 三点的转动半径依次增大,故这三个点的线速度大小也依次增大。对于曲线运动来说,线速度的定义就是运动弧长的瞬时变化率。其中,对匀速率圆周运动, 线速度等于单位时间内运动的弧长,即 v=\frac{2πr}{T} 。
再如:地球表面各个位置的自转速度都不相同。其中:① 在同一条经线的不同位置,自转速度的方向相同,但纬度越高,自转速率越小。② 在同一条纬线中的不同位置,自转速率相同,但自转速度的方向不同。

二、以题主给出的模型为例
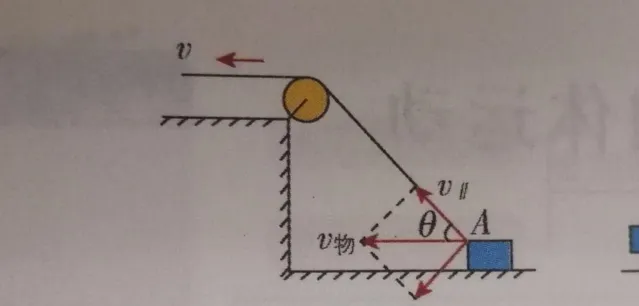
对于题主给出的这个「岸上人拉岸下物」模型来说,如果以地面为参考系,则:
① 整个运动过程中,这根绳子只有定滑轮左侧水平的部分,绳上每个点的速度都等于人拉绳子的速度 v ;而定滑轮右侧斜向下的部分始终围绕定滑轮顺时针转动,故每个点的速度都不相同。其中,绳子物端(即 绳子与物块相接的那个点)的速度刚好等于物体的速度 v_物 。
② 又由于整个运动过程中,绳子的长度保持不变(绳子始终处于绷紧状态,既没有松弛,也没有断掉),因此绳子各点沿绳子方向的分速度,其大小始终保持一致。对于这道题目,定滑轮左侧水平的部分,沿绳子方向的速度,就是它自身的速度;定滑轮右侧斜向下的部分,每个点沿绳子方向的速度,就是它沿绳子方向的分速度。
由 ①,可得 {\bf v}// {\bf v}_{物} 。即:绳子人端与绳子物端的速度方向始终保持平行。
由 ②,可得 v_{//}=v ,它起到使绳子各点依次沿定滑轮平动的运动效果,它只改变绳子每个点的路程,不改变绳子与水平面的夹角。对于任意时刻 t ,定滑轮左侧绳子增加的长度 与 定滑轮右侧斜向下减少的长度 始终保持相同,二者都等于 v_{//}\cdot t 。
v_{⊥} 起到使绳子绕定滑轮转动的运动效果,它只改变绳子与水平面的夹角 θ ,不改变绳子每个点的路程。并且,任意时刻,离定滑轮越远的位置, v_⊥ 越大。
由此可见,该题目本质上属于「绳模型」的一种具体情景。因为整个过程只涉及绳子各部分速度之间的关系。这里的「人」和「物体」仅仅用来直观、形象地反映绳子两端的速度。
联立 ①②,我们可以求出在该过程中,任意时刻船速的大小为 v_物=v/ \cosθ ,绳子船端围绕定滑轮转动的分速度大小为 v_{⊥}=v \tan θ 。
在这个问题中,绳子人端的速度 v 为定值。随着时间的推移, θ 逐渐增加, \cos θ 逐渐变小,于是绳子物端的速度 v_物 逐渐增加。故物体做水平向左的变加速直线运动。
三、一些初学者的常见误区
对于「岸上人拉岸下物」模型,一些初学者可能会错误地认为绳子上各点的速度的方向都是沿绳的。于是就将绳子物端的速度也被认为是沿绳斜向左上方的 v ,然后将其分为水平向左和竖直向上的分速度。就像这样:
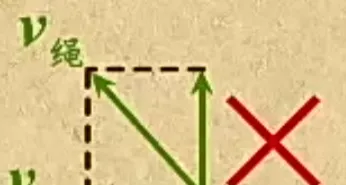
实际上,从图中,我们可以很明显地看出,整个运动过程中,绳子物端始终与物块相接。物块向左走了多少路程,绳子物端也向左走了多少路程。故绳子物端与物块的速度始终是相同的。
另外,无论是运动学问题,还是力学问题,一定要先选择参考系,要具体说明「以 XX 为参考系,……」。否则,就没有任何物理意义。 (划重点)
具体来说,「人端的绳速大小为 v_0 」是以地面为参考系得到的结论;而「船端的绳速大小为 v_0 」则是以某个随绳转动的参考系中得到的结论。但是,无论选择哪个参考系,绳子上所有点的速度都不可能相同,否则绳子就无法绕定滑轮转动。假如绳子船端相对于地面的速度就是沿绳斜向左上方的 v_0 ,则从人拉绳子的一开始,绳子的船端由于只沿绳收缩,但不围绕定滑轮转动,从而与船发生断裂。 (划重点)
————————————
我们在日常生活中经常接触到的许多关于运动的表述,从物理学的层面,其实都犯了「没有统一参考系」的错误。
譬如:我们日常讲到的「月亮围绕地球转,地球围绕太阳转」这句话,从原则上就属于不严谨、不规范的表述。
这是因为「月亮围绕地球公转」,是以地球为参考系得到的结论;而「地球围绕太阳公转」,又是以太阳为参考系得到的结论。——在物理学上,有一个默认的约定:如果没有具体说明参考系,通常默认所有的物理量都是在同一个参考系下的结果。这是因为,只有统一参考系,才能保证系统内不同对象之间的物理量关系是确定且有意义的。
• 如果以地球为参考系进行运动学分析,根据相对运动的原理,可知:如果不考虑地球的自转,月球和太阳都围绕地球自西向东以椭圆轨道做曲线运动。其中,月球的公转周期约为 27.32 天,太阳相对于地球的反向运动周期约为 365.25 天。从而,我们站在地球表面从天空中,可以看到太阳、月球都在天球上自西向东倾斜地做非匀速转动,且月球的角速度约为太阳的 13.37 倍。

• 如果以太阳为参考系进行运动学分析,有:地球围绕太阳自西向东以椭圆轨道做曲线运动,而月球围绕太阳在地球公转轨道附近做波浪线运动。——考虑到实际比例,月球的运动轨迹与地球公转的轨道几乎重合。其中,地球的公转周期约为 365.25 天,月球在地球公转轨道附近内外摆动的周期约为 27.32 天。

由此可见,通过选取不同的参考系,对太阳、地球、月球三者的运动进行描述,其运动轨迹也会大不相同。
四、杆模型
一根长直轻杆 AB 在墙角沿竖直墙和水平地面滑动。当杆 AB 与墙的夹角为 θ_{\rm A} ,与地面的夹角为 θ_{\rm B} 时,杆的 A 端沿墙下滑的速度大小为 v_{\rm A} ,杆的 B 端沿地面向右的速度大小为 v_{\rm B} 。则 v_{\rm A}:v_{\rm B} 等于多少?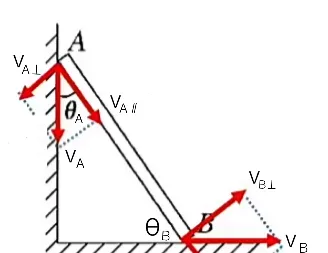
① 杆在滑动的过程中,A 端速度 v_{\rm A} 的方向始终沿墙竖直向下,B 端速度 v_{\rm B} 的方向始终沿地面水平向右。即 {\bf v}_{\rm A}⊥{\bf v}_{\rm B} 。
② 类似于题主给出的绳模型,在任意时刻,杆的长度保持不变,故杆上各点沿杆方向的分速度大小和方向始终保持一致。于是,对 A、B 两端,满足关联等式 v_{\rm A //}=v_{\rm B//} 。
杆上各点垂直于杆方向的分速度共同使杆产生转动的运动效果。其中,A 端垂直于杆的分速度 v_{\rm A ⊥} 使杆与地面的夹角 θ_{\rm B} 逐渐减小,B 端垂直于杆的分速度 v_{\rm B⊥} 使杆与墙面的夹角 θ_{\rm A} 逐渐增加。
联立 ①② 可得, v_{\rm A //}= v_{\rm A} \cos{\rm θ_A}=v_{\rm A} \sin{\rm θ_B} , v_{\rm B //}= v_{\rm B} \sin{\rm θ_A} =v_{\rm B} \cos{\rm θ_B} 。
故 \frac{v_{\rm A}}{v_{\rm B}}=\tan {\rm θ_A}=\frac{1}{\tan{\rm θ_B}} 。
五、一定都要分解成沿杆和垂直于杆的分速度吗?
用铰链固定的杆子一端连一小球,最初球靠在可自由移动的木箱上。现让箱子以速度 v_{木箱} 向右匀速运动,当杆子与竖直方向的夹角为 θ 时,小球的速度 v_{球} 是多少?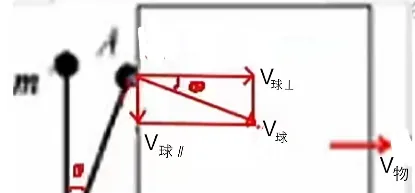
这个模型中,随着木箱向右匀速运动,从而杆相对于铰链(转轴)顺时针旋转。其中,小球的速度 v_{球} 的方向始终垂直于杆向右,故小球并没有完全沿杆方向的分速度,即 v_{球 ⊥}=v_球 ,v_{\rm 球 //}=0 。因此,这道题肯定无法利用杆上两点之间的关联加以求解。
故我们需要寻找小球与其他物体(或者其他物体上的点)之间的分速度关联。
那么,如何找到该模型中,两点分速度之间的关联呢?——它决定了我们应该将速度沿哪个方向进行分解。
由于整个过程中,小球始终靠在木箱上,故物体水平向右移动了多少位移,小球也水平向右移动了多少位移。于是,对于相互接触的两个物体之间,它们的垂直于接触面的分速度相等。故我们应将小球的速度 v_{球} 分解成垂直于接触面水平向右的分速度 v_{球 ⊥} 与沿接触面竖直向下的分速度 v_{球//} 。[为保证符号的规范性,这里仍然采用相同的分速度下标进行表示。]
对小球和木箱上的任意一点,均满足关联等式 v_{木箱}=v_{球⊥} 。
其中, v_{球⊥}=v_{球} \cos θ 。
故 v_球 = \frac{v_{木箱}}{\cos θ} 。
六、「关联等式」小结
• 对于绳关联模型,有绳子两端沿绳方向的分速度大小相等。
• 对于杆关联模型,有杆两端沿杆方向的分速度相等。
• 对于接触关联模型,有两物体垂直于接触面(切面)的分速度相等。
• 绳关联模型 与 杆关联模型 中,绳子上任意一点垂直于绳的分速度 或者 杆上任意一点垂直于杆的分速度,都满足线速度与角速度的换算公式 v_⊥ = ω \cdot r 。它起到绷紧的绳子或杆围绕某个旋转中心转动的效果,从而使绳子或杆与水平面或竖直面的夹角发生变化。
高中阶段涉及到的关联速度分解题目,大多可以归结为 以上三种基本模型的关联等式 以及 线速度与角速度的换算公式 之间的组合。










