更新:知乎小透明第一次拥有这么多赞,受宠若惊,感谢大家的点赞。笔者目前只是个学生,没有足够能力独自解决这个问题,在参考了C. E. Siewert和E. E. Burniston两位大佬的paper [1] 后才写下这篇回答。至于评论区提到的关于答案化简的问题,请参考酱紫君大佬的这篇文章 [2] ,里面包含了若干种其他形式的解析解以及相应的数值验证,在此贴出,以飨各位读者。
一、介绍
x=\cos x\Rightarrow x-\frac{\pi}{2}=\cos({x-\frac{\pi}{2}})=\sin x
这个方程的一般形式叫做 开普勒方程 ( Kepler’s equation ) [3] , 开普勒方程是天体力学研究的基础,因此几个世纪以来一直备受关注。对于椭圆轨道,开普勒方程通常写成:
e \sin E=E-M \tag{1}\\
对于双曲轨道,开普勒方程通常写成:
e \sinh F=F+N \tag{2} \\
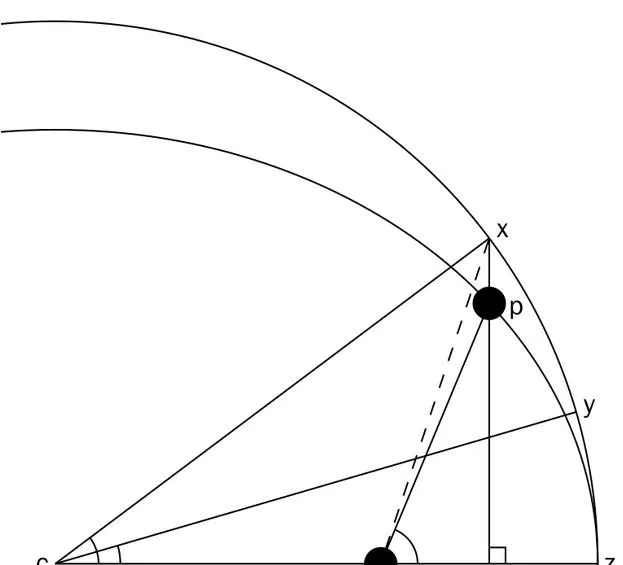
其中,辅助圆轨道上假想质点所转过的角度\angle M 被称为 平近点角 [4] ,
参考
- ^ An exact analytical solution of Kepler's Equation https://link.springer.com/article/10.1007/BF01231473
- ^ x = cos x 的解析形式 https://zhuanlan.zhihu.com/p/36297534
- ^ 开普勒方程 https://zh.wikipedia.org/zh-hans/開普勒方程
- ^ 平近点角 https://baike.baidu.com/item/平近点角/5984710










