在电路中,要表示交流电通常有两个方法。
一种是直接用函数表达式: U=V_mcos(\omega t+\varphi) 。但是这种方法基本上没有人用,因为直接用表达式计算电路问题就太复杂了。举个例子:
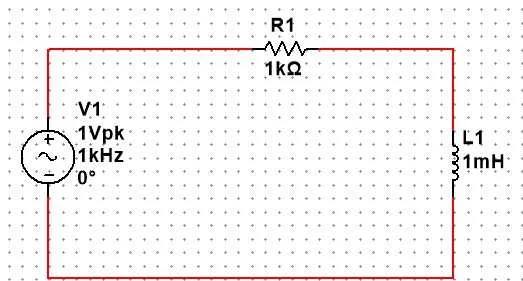
像是这样一个十分简单的电路,只有一个交流电源,一个电阻和一个电感。如果我要计算这个电路中的电流的话需要列这样一个微分方程:
L\frac{di}{dt}+Ri=V_mcos(\omega t +\varphi)
其中,又因为在含有电感的电路中,电流不能突变,所以可得到初始条件:
i|_{t=0}=0
联立解出来电流的函数表达式为i=\frac{-V_m}{\sqrt{R^2+\omega^2L^2}}cos(\varphi-\theta)e^{-\frac{R}{L}t}+\frac{V_m}{\sqrt{R^2+\omega^2L^2}}cos(\omega t+\varphi-\theta)
其中 tan\theta=\frac{\omega L}{R} 。
当时我学到这里的时候头都要炸了。其中这个微分方程的求解过程也是非常繁琐的。而且这在电路中已经算是非常非常简单的电路了,如果这个电路在稍微复杂一点,可能求出来的解就已经复杂到没有什么实际价值了。
那么有没有方法可以简化一下这个问题呢?
首先,很多时候我们并不需要求这个系统随时间变化的过程,而只是需要这个系统最后的稳态解。
像是这个例子中,我们很容易就可以发现,当时间趋向于无穷时, \lim_{t\to \infty}i=\frac{V_m}{\sqrt{R^2+\omega^2L^2}}cos(\omega t+\varphi-\theta) 。
也就是说当时间无限增大时,电流趋向于一个三角函数,前面的那一项为0。在研究一般具体的电路问题时,电路达到稳态所用的时间一般都是很短的。所以我们就很自然的想到,如果要求出稳态解,有没有什么简单的办法?
这个时候我们可以大胆想象,既然交流电的形式时三角函数,而根据欧拉公式,在复数域中三角函数又和指数函数有着千丝万缕的联系,那我们可以用一个复数来表示这个这个电压。 U=V_mcos{(\omega t+\varphi)}=V_mRe\{e^{j(\omega t+\varphi)}\}=V_mRe\{e^{j\omega t}e^{j\varphi}\} 。
在电路中,由于 i 已经用于表示电流,所以我们一般用 j 来表示虚数单位。一般来说,交流电路中的线性元件不改变电流电压的频率,所以这里我们还可以在简化,只用电压的相位角和峰值来表示电压。然后将电压的频率单独给出。所以我们用一个复数 \textbf{V} 来表示电压,并定义:
\textbf{V}=V_m(cos\varphi+jsin\varphi) 。通常简写为 V_m\angle\varphi 。同理,电流也可以表示为 I_m\angle\varphi
这样表示的最大的一个好处就在于我们可以用简单的线性关系,来描述电容和电感了。
以刚才的电感为例我们知道电感两端的电压满足 U=L\frac{di}{dt}
如果电流的变化关系为 i=I_mcos(\omega t+\varphi)
那么电压就为 U=L(-\omega I_msin(\omega t+\varphi))
稍微变化一下: U=-\omega LI_mcos(\omega t+\varphi -\frac{\pi}{2})
这时候,我们如果都用复数表示电压和电流,就可以发现:
\textbf{V}=-\omega L I_me^{j(\varphi-\frac{\pi}{2})} \hspace{14pt}\\=-\omega LI_me^{j\varphi}e^{-j\frac{\pi}{2}} \\=j\omega L I_me^{j\varphi}\\=j\omega L \textbf{I}
其中 e^{-j\frac{\pi}{2}}=cos\frac{\pi}{2}-jsin\frac{\pi}{2}=-j 。
这时候我们很神奇的看到, 如果都用复数来表示电压和电流,那么电压和电流之间就是非常简单的线性关系 。他们的比值也就被定义为感抗。
这时候我们在回到一开始的那个问题

对于电阻来说,无论什么时候电流和电压都是线性关系,比值为 R 。而电感两端的电压电流之比如果用复数来表述,也是一个定值 j\omega L 。那么电流就可以简单的用电压和电抗的比值来求:
i=\frac{V_m\angle\varphi}{R+j\omega L}=\frac{V_m\angle\varphi}{\sqrt{R^2+\omega^2 L^2}\angle \theta}=\frac{V_m}{\sqrt{R^2+\omega^2 L^2}}\angle \varphi-\angle\theta 。
这里我简写了一下,因为复数的运算时模相除,角相减。
再把它化成函数表达式的形式就是 i=\frac{V_m}{\sqrt{R^2+\omega^2L^2}}cos(\omega t+\varphi-\theta) ,和之前用微分方程求出的结果一样。
很显然,我们的计算过程被大幅简化了。
用复数表示交变电流的好处还不止于此,希望你以后也可以自己多多了解一下。











