背景介绍:
一般而言,如果在空旷环境下,GNSS的定位精度已经很高,也就没有很高的必要性考虑利用5G信号进行定位。
相对而言,就亟需在城市化的环境下,比较GNSS和5G的定位性能。在这种场景下,对GNSS/5G定位造成主要影响的就是多路径干扰——众所周知,GNSS多路径误差一般几米~几百米不等。接收机利用一些传统的抗多径干扰算法,可以很容易地抑制大于约20米以上多径误差。根据一些最新的研究成果显示,5G信号的多径误差,在仿真条件下,至少也在米级范围 [1] ,与GNSS的误差范围相近。
通常情况下,用户相对于5G基站/GNSS卫星的仰角越低,观测量中存在多径误差的概率越大,具体的发生过程,可以参考下面两幅示意图:
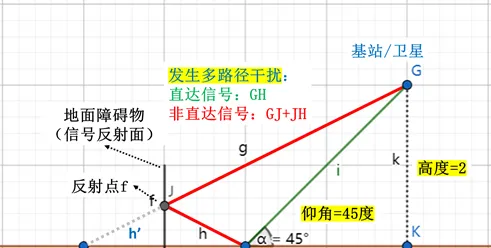
当基站/卫星与用户镜像点的连线穿过地面障碍物的横截面,此时就会在用户端发生多径干扰。
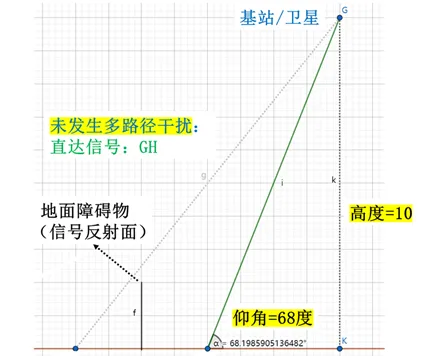
当基站/卫星的高度增加,此时它们相对于用户的仰角也变大。观察示意图发现,仰角越大,多路径干扰发生的概率越小(因为基站/卫星与用户镜像点的连线穿过地面障碍物横截面的概率变小了)。
5G信号的基站高度一般为几十米,这就导致用户相对其仰角一般比较低。从全球范围来看,GNSS卫星可以覆盖用户0~90度的仰角范围,因此,GNSS信号相对于5G信号在城市环境下,理论上,发生多径干扰的概率更小。
一些假设
根据以上分析,我们可以在给出以下假设的前提下,定量地比较GNSS/5G的定位精度:
假设一:
为了简化分析,忽略高程位置,只考虑用户水平面内的二维位置坐标;
假设二:
5G基站和GNSS卫星几何构型一致,如下图所示:

假设三:
GNSS和5G信号的多径误差在0~20m的范围内;
假设四:
当5G基站/GNSS卫星的仰角不大于20度时,一定发生多路径干扰;当仰角大于20度时,则不会发生多径干扰;
假设五:
不考虑时钟及其他随机噪声对定位精度的影响。
利用最小二乘计算用户位置
{\mathbf{x}} = {\left[ {{x_r},{y_r}} \right]^T}
用户到卫星A的距离函数为
l_r^{\left( A \right)} = \sqrt {{{\left( {{x^{\left( A \right)}} - {x_r}} \right)}^2} + {{\left( {{y^{\left( A \right)}} - {y_r}} \right)}^2}}
其中, \left( {{x^{\left( A \right)}},{y^{\left( A \right)}}} \right) 表示卫星A的位置坐标。
为了利用最小二乘求解用户位置,必须要将上面的模型进行线性化(利用泰勒展开),得到:
l_r^{\left( A \right)} \approx {r^{\left( A \right)}} + {\left. {\frac{{\partial l_r^{\left( A \right)}}}{{\partial {x_r}}}} \right|_{{x_r} = {x_0}}}\left( {{x_r} - {x_0}} \right) + {\left. {\frac{{\partial l_r^{\left( A \right)}}}{{\partial {y_r}}}} \right|_{{y_r} = {x_0}}}\left( {{y_r} - {y_0}} \right)
其中,
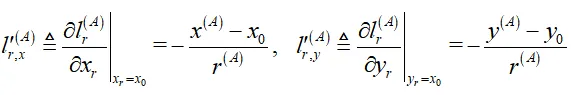
并且 {r^{\left( A \right)}} 表示用户到卫星A的几何距离; {\mathbf{x}} = \left[ {{x_0},{y_0}} \right]^T 表示用户位置初始值。
综上,观测矩阵和观测量向量分别为
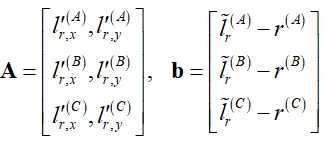
\delta {\mathbf{x}} = {\left( {{{\mathbf{A}}^T}{\mathbf{A}}} \right)^{ - 1}}{{\mathbf{A}}^T}{\mathbf{b}}
{\mathbf{x}} = {{\mathbf{x}}_0} + \delta {\mathbf{x}}
构造存在多径误差的观测量
\tilde l_r^{\left( A \right)}{\text{ = }}\sqrt {{{\left( {{x^{\left( A \right)}} - {x_r}} \right)}^2} + {{\left( {{y^{\left( A \right)}} - {y_r}} \right)}^2}} + {B_{mul}}
其中, \left[ {{x^{\left( A \right)}},{y^{\left( A \right)}}} \right] 和 \left[ {{x_r},{y_r}} \right] 在这里都表示真实的卫星位置和用户位置坐标;
{B_{mul}} 表示多径误差(这里考虑0~20m范围内的随机值)。
仿真实验及结果
根据「一些假设」一节中的讨论,利用简单的仿真实验来比较GNSS信号和5G信号在城市环境下的定位精度。
| 仿真参数 | 设定值 |
| 产生多径仰角范围 | 0~20度 (超过20度则无多径发生) |
| 5G基站的最大仰角 | 30, 40, 50, 60, 70, 80度 |
| GNSS卫星的最大仰角 | 90度 |
| 多径误差的范围 | 0~20米 |
| 蒙特卡罗实验次数 | 10000次 |
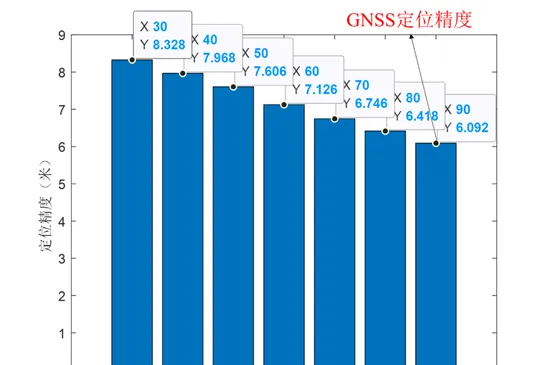
下面两图展示了最终的仿真结果。根据仿真结果判断,5G基站的最大仰角(或基站高度)越高,定位精度越高。GNSS在仿真中的定位精度最高,约6米;随着5G基站最高仰角的增加,其定位精度也逐渐提高;当基站的最高仰角为30度时,GNSS相对于5G定位精度有26.86%的提升,当仰角增大到80度时,提升程度变小,仅为5%左右。

结论
这个回答,定量分析了城市环境下,多路径对GNSS信号和5G信号定位精度的影响。用户相对于GNSS卫星或5G基站的仰角,影响着两种无线信号发生多路径干扰的概率。为了能具体分析定位精度,回答中,对仿真实验进行了大量简化,设定了很多假设,实验参数设置了很多限制条件,可能在实际环境下,有些假设并不能严格满足,因此实验结果仅供参考。但可以确定的是,如果不能很好地解决多路径对5G信号定位的影响,在短时间内,其定位精度还是没有办法超越GNSS。
参考
- ^ K. Shamaei, 「Exploiting Cellular Signals for Navigation: 4G to 5G,」 University of California, Irvine, Irvine, 2020.
- ^ 谢钢, GPS原理与接收机设计. 北京: 电子工业出版社, 2009.











