在我们日常生活中，数字通常都很「实用」，用于计数或测量，范围也相对容易理解。然而，在数学、计算机科学、天文学等领域里，有时会遇到那些超乎常人想象的「大数」。这些数如此之大，以至于仅用常规的数学符号和语言都难以表达。例如，你可能听说过「哥德尔数」、「格雷厄姆数」或是「忙碌海狸数」，这些都是巨大到几乎无法想象的数字。它们不仅仅是抽象概念，实际上，这些「大数」在理论计算机科学、逻辑学，甚至哲学问题如无限性和可计算性等方面都有着重要的应用和深远的意义。
这其中有一部分非常引人注目，那就是忙碌海狸数（Busy Beaver）和TREE之间的比较，
Tree 数（TREE(n)）是一个用于描述特定类型的树结构「大小」的数学序列。该序列在数学逻辑和 Ramsey 理论中有重要应用。尽管 TREE（1）和TREE（2）是相对较小的数，TREE（3）已经大到无法用常规数学表示法描述，远超过诸如格雷厄姆数这样的已知大数。这些数因其难以想象的「大小」和数学复杂性而受到广泛关注。
当你深入研究忙碌海狸数时，会发现这可能是存在的最令人震惊的函数。 实际上，理论上没有任何算法能够生成与这一函数匹配的数字。
如果有某种神奇的暴力计算方法能计算出忙碌海狸函数的一些小的输入值，那将涉及解决数学中几个世纪以来未解决的问题。有些数学体系在达到某个点后甚至无法证明其值。这个数，实际上就是一串固定的数字，很明确地划分了可计算和（Computable）不可计算（Not Computable）的界限。
我对这还不是很了解。这里主要引用Scott Aronson和其他几位数学家的工作，
首先，我们需要了解 二进制图灵机 （Binary Turing Machine）。这是一种抽象设备，作用于一个由1和0构成的无限长的纸带上。
这台机器有一个内部状态，它读取一个单元，然后根据其状态和所读内容写入1或0，然后向左或右移动，并转换到一个新状态。也可能停止计算。
为了表示机器的所有行为，我们使用一个状态表。这是一个四态机器，因为它有四个不同的状态（不包括停止状态）。对于状态和读取值的每一种组合，都有三种动作：写入的值，如何移动，以及转换到什么状态。
例如，如果机器处于状态A并读取一个值为0的数据，那么我们会在上图红色框中（1、L、D）查找以确定接下来的动作。在这种情况下，我们会写入一个值为1的数据，向左移动，并将状态切换到D。
然后，我们需要了解两件关于图灵机的事情。首先，Church-Turing论文指出， 任何计算（即应用于某些输入以产生某些输出的任何有限步骤序列）都等价于某个图灵机的操作 。这意味着，我们可以把所有的计算，所有的算法都看作是图灵机，无论是Python函数，C++程序，还是你的电脑正在执行的任何事情。
其次，图灵证明了 不存在一种算法，能接受任何状态表和任何输入纸带作为输入，并判定机器是否会在该纸带上停止。这样的问题是不可判定的。
没有通用的方式可以简单地预判一个计算是否会终止，有时必须运行它并等待，而且可能会永远地等下去，永远都不知道答案。值得强调的是， 没有一个单一的算法能适用于所有机器和纸带。 在某些特定的机器和纸带情况下，或许有专门的算法能决定它是否会停止。
那么，什么是 忙碌海狸函数呢（The busy beaver function） ？我们将其记作
实现这个最大值的机器被称为忙碌海狸机器。
举个例子，假设n等于2，考虑一个有两个状态的表。
通过某个特定的图灵机，最终纸带上可能写下两个1。
但事实证明，如果用另一台图灵机，会得到四个1，
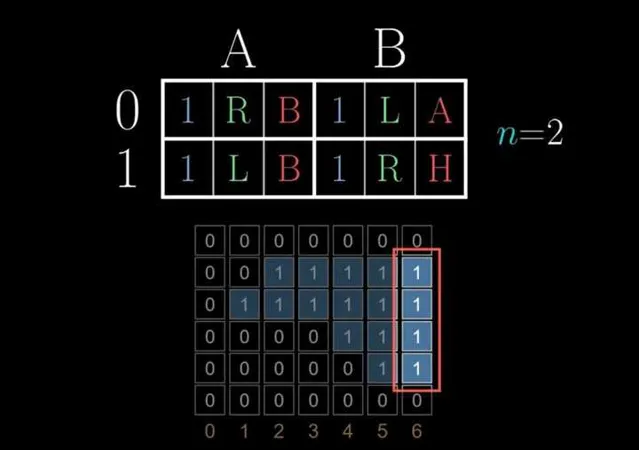
这是最多的，所以Σ（2）是4。
这个过程是如何继续的呢？对于三状态的图灵机，最终纸带上最多有六个1，所以Σ（3）是6；对于四状态的图灵机，最多有13个1，所以Σ（4）是13。 至于五状态的图灵机，人类至今还无法计算这个数。
为什么这么难计算呢？我们来看看有多少种n状态的图灵机，
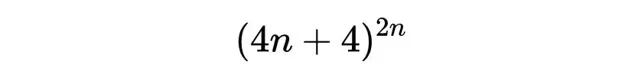
数量是这么多。可以看到，随着所考虑的状态数量的增加，机器的数量是呈指数增长的。当有四个状态时，那涉及到超过250亿台图灵机，而人类确定了它们能写入的1的最大数量是13，这已经是一项非常艰巨的工作。
问题在于判定哪些机器会停止，没有通用的算法。
因此，我们需要对单个机器进行多年的理论推断，找出最终会停止的一小部分机器，并运行它们以得出写入1的最大次数。对于五状态的图灵机，这涉及到数万亿台更为复杂的机器。
这个函数有多难呢？首先， Σ(n)甚至不是一个可计算的函数 。一个可计算的函数是那种可以通过有限步骤从输入产生输出的函数，但这里没有这样的函数，因为有些机器会永远运行。在整个运行过程中，我们可能会认为其中一台机器可能是「忙碌的海狸」（Busy Beaver）。
「忙碌的海狸」是一个来自计算理论的概念，用于描述一个特殊类型的图灵机，这种图灵机在给定状态数的限制下，能够在最终停机（halt）之前打印出尽可能多的「1」。那么，我们怎么能计算像Σ（4）这样的数呢？这里有一点微妙之处： 不可计算性来自于缺乏一种适用于所有n的有限程序 。但对于特定的n，由于机器数量是有限的，我们可能能够通过分析找到答案。
有证据表明， 这个序列增长速度超过任何可计算的函数 。 换句话说，在所有可能的函数中，只要输入一个整数n并在有限时间内返回一个整数，忙碌海狸函数在某个n值之后的增长速度将超过它。
这实在是太不可思议了。简单地说，任何你能想象到的通过有限步骤处理输入的方式，都无法超过这一令人惊叹的数列。
尝试挑战王者
让我们尝试挑战忙碌海狸函数。我将构造一个自己的快速增长的函数。首先，我要发明一些符号。假设一个问号代表一个阶乘的指数版本。比如4问号，是指4的3次方的2次方的1次方。
从右上角开始向下求值，大约等于262,000，这对于4来说是一个相当大的数字。
现在考虑这个，
得到了一个高达262,000项的指数塔。所以两个问号后，就得到了一个无用的大数。
接下来，我定义破折号问号，
如果应用到4上，那就是4带着很多问号，
具体有多少个呢？那将是4问号个问号，
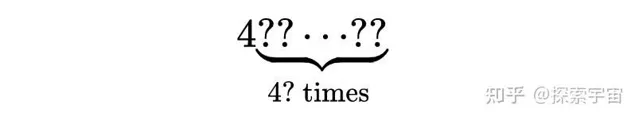
这简直太疯狂了。我们再进一步，定义双破折号问号，
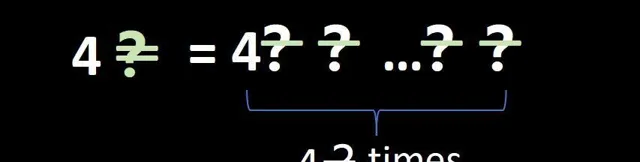
要明确的是，从左边开始求值，也就是从 4破折号问号 开始，然后把这个数再次代入破折号问号，得到一个超乎想象的数，而且要这样做很多很多次，实际上要做无数次。
现在，我尝试用这个去推翻忙碌海狸函数，
效果如何呢？根本不接近！当然，对于小的n，我定义的数是更大的，但一旦超过了某个界限，忙碌海狸函数就会完全碾压。
但临界点在哪里？我们可以用更快增长的 格雷厄姆数g_n（（Graham's number）） 来做一些估计，这是一个比我定义的数增长得更快的数，
格雷厄姆数（Graham's number）是一个非常大的自然数，由数学家罗纳德·格雷厄姆（Ronald Graham）在解决一个特定的组合优化问题时引入。这个数是如此之大，以至于不能用常规的数学符号或科学记数法来表示。
我猜测，在n大概为10的时候，Σ（n）可能会超过我定义的数，仅仅是猜测，如果实际上是8，我也不会感到惊讶。重点是，几乎是一开始，忙碌海狸数就已经打败了我的定义的数了。
我们知道忙碌海狸数超过了我定义的数，因为我定义的数是可计算的 ，即通过有限步骤从输入得到输出。
事情变得越来越怪异和抽象。 事实上，存在一个27状态的图灵机，只有当著名的「哥德巴赫猜想」是错误的时才会停止。 这个猜想是数学中最古老、最著名的未解问题之一，它指出大于2的每一个偶数都是两个质数的和，但至今无人证明。
这意味着，如果直接计算Σ（27），涉及到判断哪些机器会停止，那就相当于解决了哥德巴赫猜想。 因为我们需要确定哥德巴赫图灵机是否停止：如果停止，猜想就是错误的；否则就是正确的。黎曼猜想也是同样的道理。
准确地说，也许有一些计算忙碌海狸数但不实际解决这些开放问题的奇怪途径，但这不是重点。重点是这些数包含了大量的数学信息，实际上情况还会变得更加复杂。
其数值在某些体系中无法被证明
更奇怪的是，事实证明有些真实的命题，比如说Σ（1000）等于某个数K，
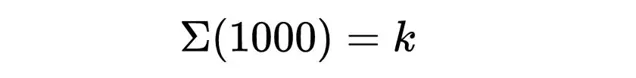
在我们常用的数学公理体系中无法被证明。 也就是说，到了某一点，数学失去了对这些数字作出声明的能力。
