我來寫個帶推導過程的答案吧。2048的玩法就不贅述了,先來看看相關的規則,因為是Gabriele Cirulli讓這個遊戲火起來的,以他的原始碼為準(Gabriele Cirulli的版本的地址:
2048)。
記分規則 :在
2048/game_manager.js at master · gabrielecirulli/2048 · GitHub中的167行:
self
.
score
+=
merged
.
value
;
分數就是累加遊戲過程中新合成方塊的數值。
新方塊出現的規則 :在
2048/game_manager.js at master · gabrielecirulli/2048 · GitHub的71行:
var
value
=
Math
.
random
()
<
0.9
?
2
:
4
;
新方塊的取值集為{2, 4},其中4出現的機率是0.1。
題主的第一問: 如果到2048不繼續,那麽最高分是多少?
2048肯定是由兩個1024合成的,所以在合成2048的這一步,記分是2048,同樣1024也是由合成得到的,所以在得到兩個1024的這兩步,積分是1024*2=2048,以此類推,在>4的情況下,每一步分解的逆過程都會積2048分。註意到題主問的是理論最高分,我們當然希望盡可能多的合成新方塊,所以不希望4是直接生成的,應該都是由2合成的。假設題主運氣足夠好,玩的過程中出現的新方塊都是2,那麽基於以上推導,從2一路合成到2048,理論上的最高分為:
\[2048\times \left( {{\log }_{2}}\left( 2048 \right)-{{\log }_{2}}\left( 2 \right) \right)={{2}^{11}}\times \left( 11-1 \right)=\text{20480}\]
對於任意從2開始合成的\[{{2}^{N}}\] 這個公式可以推廣為:
\[{{2}^{N}}\times \left( N-1 \right)\]
題主的第二問: 如果繼續,那麽最高分是多少?
要回答這個問題首先要來看2048理論上能達到最終布局是怎麽樣的,假設能達到的最大的數值為\[{{2}^{N}}\] ,那麽在最後一步合成\[{{2}^{N}}\] 時一定是占兩格的兩個\[{{2}^{N-1}}\] ,那麽對這兩個\[{{2}^{N-1}}\] 做最小的展開,也就是保持一個不變,另一個展開為兩個\[{{2}^{N-2}}\] ……如下所示:
\[{{2}^{N}}\xleftarrow{\text{merge}}{{2}^{N-1}},{{2}^{N-1}}\xleftarrow{\text{merge}}{{2}^{N-1}},{{2}^{N-2}},{{2}^{N-2}}\xleftarrow{\text{merge}}\cdots \xleftarrow{\text{merge}}{{2}^{N-1}},{{2}^{N-2}},\cdots 16,8,4,4\]
所以依次類推如果要合成\[{{2}^{N}}\] ,則需要一直展開一個相鄰的方塊序列直到遊戲能產生的方塊值,其中序列長度由要展開的級數的初始值決定,比如要展開到\[{{2}^{N-M}}\] ,則需要的序列長度是\[M+1\] ,因為遊戲一共16個格子,所以\[M+1=16\] ,則\[M=15\] 。考慮到需要最大值,所以認為在這樣一個序列中,遊戲產生的方塊是兩個4,那麽\[{{2}^{N-M}}={{2}^{N-15}}={{2}^{2}}=4\] ,則\[N=17\] ,所以遊戲能達到的方塊最大值是\[{{2}^{17}}=\text{131072}\] 。同樣道理,當一個131072已經產生之後,還剩下15個格子,那麽這種情況下能產生的最大值為65536,依此類推,14個格子能合成的最大值是32768,……所以理論上最大值的情況一定是前15個格子的值依次為\[{{2}^{17}},{{2}^{16}},{{2}^{15}},\cdots ,{{2}^{4}},{{2}^{3}}\] ,也就是\[131072,65536,32768,\cdots ,16,8\] ,而最後一個格子是2或者4。前面好多答主也貼過最後的局面,我這裏也貼一例(圖用我自己寫的
蛋疼99行程式碼Python版2048畫的):
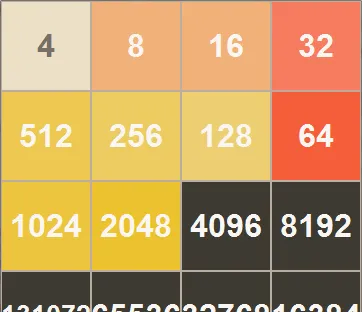
因為最後一個4或者2是遊戲產生的,所以不計入積分,所以所有的積分都來源於從8到131072的15個數位。回想在第一問裏得到的從2開始合成\[{{2}^{N}}\] 的公式,那麽似乎最高分應該是N=3,4,5,...,16,17對應的積分的總和,也就是
\[\sum\limits_{K=3}^{17}{{{2}^{K}}\times \left( K-1 \right)}=\text{3932160}\]
這個答案前面有幾位答主也提到過,然而,這個答案是不對的,原因就是上面我關於合成數值的最小格子數占用的分析,當65536合成之後,從2開始合成一個數值需要的最少格子數超過了可用格子數了。比如我們考慮要合成兩個65536的情況,也就是第一次合成出131072的情況,如下圖:

這是合成出131072必經的一步,註意最左上角的4,這個4顯然不可能是由2合成的,而是遊戲直接生成,因為對於131072,從4開始合成最少需要的格子數是16,所以只有在需要合成的值是65536或者以下時,我們才有可能從2開始合成出所有的數值,也就是說對於2048這個遊戲,只有當\[N\le 16\] 時\[{{2}^{N}}\times \left( N-1 \right)\] 才成立。也有其他答主發現了這個問題,所以有答主說,多算了一個4,答案是3932160-4=3932156;另有答主說是3932152,也許考慮的是多算了兩個4的情況;然而這幾個分數都是無法得到的,關鍵就在於 要產生多少個值為4的方塊,那麽最後就得從3932160的分數裏減去多少個4 。
那麽什麽時候需要遊戲必須產生4呢,我們再回到前面關於產生一個數值需要序列長度的推導:前面得出的結論是要展開到\[{{2}^{N-M}}\] ,則需要的序列長度是\[M+1\] ,因為我們希望合成次數盡量最大化,所以要展開到\[{{2}^{N-M}}=2={{2}^{1}}\] ,則需要的格子數目為\[M+1=N\] ,所以在\[{{2}^{17}}=131072\] 出現前,任何數位都不會需要16個以上的格子,所以也就不需要4的出現。而當需要合成131072時,需要17個格子,而整個遊戲只有16個,所以就不能從2開始合成了,於是這是第一次需要4的情況。當131072已經出現後,可用格子的最大數目是15了,這時候合成\[{{2}^{16}}=65536\] 也需要一次4了。當65536合成之後,可用格子最大數目變為14,這時候32768的合成也需要產生一個值為4的方塊了……於是依次類推,當16合成之後(也用到了新產生的值為4的方塊),為了合成8,最後一次由遊戲產生了4,也就是下圖:

所以從8到131072,一共15個數位在最後合成的過程中需要4的出現,也就是說理論上能達到的最高分數是:
\[\text{3932160-4}\times \text{15=3932100}\]
這個答案前面一位答主應該也提到過,雖然沒有推導過程。
當然了,這個畢竟是理論最高分,實際操作起來,幾乎是無法達到的,透過不斷的悔棋和堅強的毅力達到我前面提過的最終局面也許並不難,但是2和4出現的比率是9:1這點是無法透過悔棋改變。不妨大概估算一下,對於\[{{2}^{N}}\] 可以算出需要\[{{2}^{N-1}}\] 個值為2的方塊,那麽對於最終局面,如果不考慮格子數目對生成4的限制,則一共需要:
\[\sum\limits_{K=3}^{17}{{{2}^{K-1}}}={{2}^{17}}-{{2}^{2}}=\text{131068}\]
這麽多值為2的方塊,減去最後15個必須的值為4的方塊,並考慮由於10%的4會生成,並且一個4等價於2個2,所以實際遊戲當中玩到最終局面平均生成的方塊數目為:
\[\left( 131068-15\times 2 \right)\div 1.1\approx \text{119125}\]
則值為4的方塊平均數目約為11915,所以少產生的分數為:
\[\text{11912}\text{.5}\times 4\approx \text{47650}\]
也就是說如果玩到了理論上方塊值最大的情況,平均分大約會是
\[3932100-47650=\text{3884450}\]
考慮到4出現的過程是個服從卜瓦松分布,而在數目這麽大的情況下可以用高斯分布來近似,如果很不嚴格地忽略掉4出現得漲落對總方塊數目的影響,則有
\[\sigma {{N}_{4}}\approx \sqrt{11915}\approx \text{109}\]
所以大部份分數會落在以下範圍:
\[3884450\pm 3\times 109\times 4=3884450\pm 1308\]
我大概在網上搜了一下,發現玩到最終局面的大都分為兩種情況,一種是和我推導的一致在3884450左右的分數,還有一種是在386????附近,是因為Practice mode積分方法不同?版本不同?還是什麽別的原因,不太清楚了。








