聊一下遊戲。
為了避免歧義,我們先定義閃避率和減傷,按最大眾化的理解:
10%閃避率=受到傷害時有10%的機率完全規避這次傷害
10%減傷=受到的所有傷害降低10%
結論1:理想模型下,相同初始條件時,兩個內容價值相同。
我們先建立最簡單的理想模型:
- 只考慮有HP(生命值)與ATK(攻擊力)兩種內容
- 每受到一次攻擊,被攻擊方的HP會減少,即受到傷害,傷害值=攻擊方的ATK
- 當被攻擊方的HP=0時,被擊敗
在討論下一步之前,我們還需要引入一個EHP(有效生命)的概念:
EHP=HP歸零時累計受到的減免前傷害值(不考慮溢位傷害,就是說剛好受到那麽多傷害就死了)
EHP的意義是表示實際擊敗一個單位需要付出的代價,換句話說也就是,有多抗打。
有了EHP的概念,我們就可以定義怎麽叫做『更強』。
與生存相關的一切內容,我們都可以換算成為EHP,閃避率和減傷率也不例外。 如果某個屬效能夠提升更多的EHP,那我們就可以認為這種內容更強。
首先我們看減傷率與EHP的關系可以表示為:
EHP=HP/(1-減傷率)
當減傷率=0時,EHP=HP,也就是我們上面建立的理想模型。
當減傷率提升時,EHP也隨之提升,趨勢曲線大致如下:
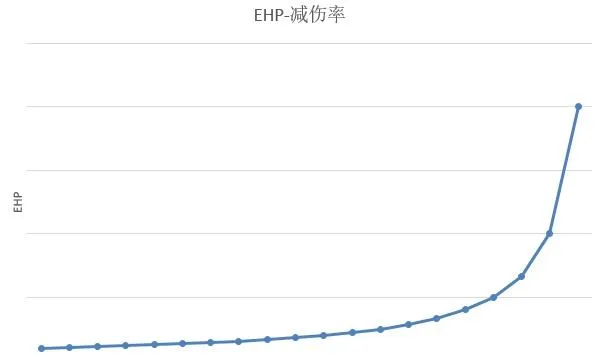
從這條曲線可以看到,每提升1%的減傷率,獲得的EHP提升是不同的。 初始減傷率越高,提升減傷率的收益就越高
然後我們看閃避率,其實從EHP的角度來說,閃避率與減傷率的計算方式完全一致:
EHP=HP/(1-閃避率)
當閃避率=0時,EHP=HP,回歸理想模型。
當閃避率提升時,EHP的提升曲線與減傷率相同:
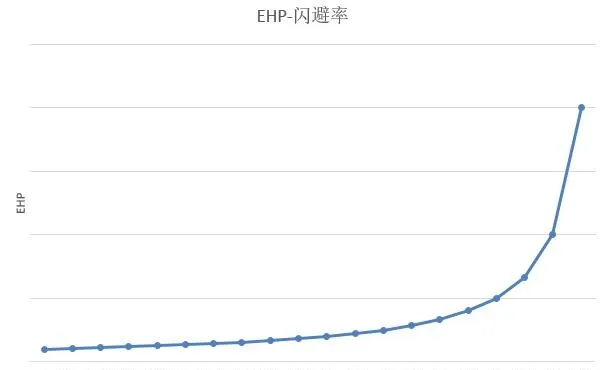
因此,如果我們考慮一個理想模型下的角色,只有HP沒有其他內容,那麽此時給他10%的減傷率和10%的閃避率,在EHP上的提升都是相同的。
結論2:大部份情況下,我們更偏好穩定的內容,減傷率更加珍貴。
玩過魔獸世界裏坦克的玩家都知道,如果堆血甲可行,那就一定不要去堆閃避。為什麽?因為就算你閃避50%,被BOSS一刀打到臉那就等於0,拼臉的事情,大家都不喜歡,除非你覺得自己可以一輩子都投色子出6點。
這就是一個很自然的人性,如果兩個東西擁有相同的價值,大部份人會更偏好穩定,大起大落不是每個人都能接受。
減傷率就是一個完全確定的內容,減少多少傷害,白紙黑字,你可以完全估計出來。
閃避率就是一個波動的內容,減少多少傷害取決於機率,而機率這種東西,有時會讓你懷疑人生。
但其實某些情況,玩家會更喜歡閃避率這種波動的內容,一個典型的場景就是以小博大。
當對手的攻擊內容遠超你的防禦內容的時候,比如你只有100血而對手有1000攻擊力,這時候減傷率的部份提升已經變得完全無用,如果想要取勝,那就只有搏一搏,期待能夠閃避掉對手的攻擊,從而爭取到更多的機會擊敗對手。
當確定的事情已經是bad ending,那就只有搏一搏,單車變摩托。
結論3:實際遊戲設計中,百分比內容的投放都比較謹慎,一般會做一次換算。
實際設計遊戲內容的時候,直接投放10%的閃避率和減傷率都是很離譜的,因為他們是非線性的。
原因就像在結論1裏的那兩幅圖,如果一個玩家初始減傷率已經有85%,那你再給他投放10%的減傷,EHP都得飆到天上,一個人打幾十個不是夢。而如果他沒有初始減傷率,那這10%的減傷就不疼不癢,聊勝於無。
理想情況,我們會希望投放內容對能力的提升是線性的,這樣無論玩家的初始內容如何,每提升一點內容,產生的價值都是一致的。
拿減傷率來舉例子,我們實際投放的減傷率,會透過一個叫做『護甲』(Def)的中間內容來實作,而一般護甲與減傷率的換算關系如下:
減傷率=Def/(M*Def+N)
其中M和N是常數,我們把這個減傷率帶入結論1的EHP公式裏,可得:
EHP=HP/(1-減傷率)=HP/(1-(Def/(M*Def+N)
為了方便計算,我們令M=N=1,則可得到:
EHP=HP(1+Def)
假設HP=100,護甲-EHP的提升曲線可以表示為:
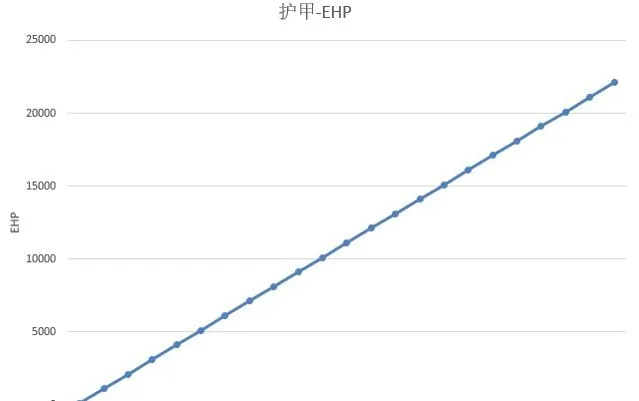
此時可以看到,這是一個簡單的線性關系,每提升一點護甲,EHP的提升都是恒定的,不依賴於玩家的初始護甲是多少。這樣價值恒定的內容投放,就可以有效避免很多問題。
同理,你現在也很少見到百分比閃避率/暴擊率的投放,一般都會換算成閃避/暴擊等級,這樣即使遊戲後期內容投放再多,它們的價值也是恒定的,不會發生越過某個節點價值躍升的設計缺陷。
最後聊聊所謂的內容價效比
在遊戲裏,資源是有限的,內容應該怎麽堆價效比才最高?這是很多數值遊戲裏一個永恒的話題,也是玩康寶此不疲討論的點。
還是以這個閃避和減傷的內容為例,假設我們投放的是閃避等級和護甲,他們對EHP的提升曲線完全相同,那是不是可以說不管怎麽堆疊,價效比都是一樣的?
我們還是回到EHP來,當考慮閃避和減傷兩個內容後,公式可以寫作:
EHP=HP*1/(1-閃避率)*1/(1-減傷率)
按結論3中的簡化公式:
閃避率=閃避等級/(1+閃避等級)
減傷率=護甲/(1+護甲)
帶入後可得:
EHP=HP*(1+護甲)*(1+閃避等級)
此時,在HP一定的前提下,EHP就相當於以護甲和閃避等級為邊圍成的矩形的面積。我們都知道邊長一定的前提下,正方形的面積最大,因此此時合理的堆疊方式,就是讓護甲和閃避等級盡量相等。
這就是我們在聊『價效比』的時候,的一種最簡單的設計策略。
實際情況內容會更多,參數價值也各不一致,但從設計意圖上,我們需要讓每一種內容都有具體的價值。
平衡堆疊多種內容,在不同的時期選擇堆疊不同的內容,發掘有限資源下提升最大的內容堆疊方式,才能有遊戲的樂趣。











