我怎麽會寫得那麽長……如果您有興趣可以和我一塊把公式過一遍。
要講清這個問題,得從狀態估計理論來說。先擺上一句名言:
狀態估計乃傳感器之本質。(To understand the need for state estimation is to understand the nature of sensors.)任何傳感器,雷射也好,視覺也好,整個SLAM系統也好,要解決的問題只有一個: 如何透過數據來估計自身狀態。 每種傳感器的測量模型不一樣,它們的精度也不一樣。換句話說,狀態估計問題,也就是「 如何最好地使用傳感器數據 」。可以說,SLAM是狀態估計的一個特例。
===================== 離散時間系統的狀態估計 ======================
記機器人在各時刻的狀態為x_1,\ldots,x_k ,其中k 是離散時間下標。在SLAM中,我們通常要估計機器人的位置,那麽系統的狀態就指的是機器人的位姿。用兩個方程式來描述狀態估計問題:
\[\left\{ \begin{array}{l} {x_k} = f\left( {{x_{k - 1}},{u_k},{w_k}} \right)\\ {y_k} = g\left( {{x_k},{n_k}} \right) \end{array} \right.\]
解釋一下變量:
f -運動方程式
u - 輸入
w - 輸入雜訊
g - 觀測方程式
y - 觀測數據
n - 觀測雜訊
運動方程式描述了狀態x_{k-1} 是怎麽變到x_k 的,而觀測方程式描述的是從x_k 是怎麽得到觀察數據y_k 的。
請註意這是一種抽象的寫法。當你有實際的機器人,實際的傳感器時,方程式的形式就會變得具體,也就是所謂的 參數化 。例如,當我們關心機器人空間位置時,可以取x_k = [x,y,z]_k 。進而,機器人攜帶了裏程計,能夠得到兩個時間間隔中的相對運動,像這樣\Delta x_k=[\Delta x, \Delta y, \Delta z]_k ,那麽運動方程式就變為:
x_{k+1}=x_k+\Delta x_k+w_k
同理,觀測方程式也隨傳感器的具體資訊而變。例如雷射傳感器可以得到空間點離機器人的距離和角度,記為y_k=[r,\theta]_k ,那麽觀測方程式為:
\[{\left[ \begin{array}{l} r\\ \theta \end{array} \right]_k} = \left[ \begin{array}{l} \sqrt {{{\left\| {{x_k} - {L_k}} \right\|}_2}} \\ {\tan ^{ - 1}}\frac{{{L_{k,y}} - {x_{k,y}}}}{{{L_{k,x}} - {x_{k,x}}}} \end{array} \right] + {n_k}\] ,其中L_k=[L_{k,x},L_{k,y}] 是一個2D路標點。
舉這幾個例子是為了說明, 運動方程式和觀測方程式具體形式是會變化的 。但是,我們想討論更一般的問題:當我不限制傳感器的具體形式時,能否設計一種方式,從已知的u,y (輸入和觀測數據)從,估計出x 呢?
這就是最一般的狀態估計問題。我們會根據f,g 是否線性,把它們分為 線性/非線性系統 。同時,對於雜訊w,n ,根據它們是否為高斯分布,分為 高斯/非高斯雜訊 系統。最一般的,也是最困難的問題,是非線性-非高斯(NLNG, Nonlinear-Non Gaussian)的狀態估計。下面先說最簡單的情況:線性高斯系統。
===================== 線性高斯系統 ============================
線性高斯系統(LG,Linear Gaussian)
線上性高斯系統中,運動方程式、觀測方程式是線性的,且兩個雜訊項服從零均值的高斯分布。這是最簡單的情況。簡單在哪裏呢?主要是因為 高斯分布經過線性變換之後仍為高斯分布 。而對於一個高斯分布,只要計算出它的一階和二階矩,就可以描述它(高斯分布只有兩個參數\mu, \Sigma )。
線性系統形式如下:
\left\{ \begin{array}{l} {x_k} = {A_{k - 1}}{x_{k - 1}} + {u_k} + {w_k}\\ {y_k} = {C_k}{x_k} + {n_k}\\ {w_k}\sim N\left( {0,{Q_k}} \right)\\ {n_k}\sim N(0,{R_k}) \end{array} \right. 其中Q_k,R_k 是兩個雜訊項的共變異數矩陣。A,C 為轉移矩陣和觀測矩陣。
對LG系統,可以用貝葉斯法則,計算x 的後驗機率分布——這條路直接通向 卡爾曼濾波器 。卡爾曼是線性系統的遞推形式(recursive,也就是從x_{k-1} 估計x_k )的無偏最優估計。由於解釋EKF和UKF都得用它,所以我們來推一推。如果讀者不感興趣,可以跳過公式推導環節。
符號:用\hat{x} 表示x 的後驗機率,用\[\tilde x\] 表示它的先驗機率。因為系統是線性的,雜訊是高斯的,所以狀態也服從高斯分布,需要計算它的均值和共變異數矩陣。記第k 時刻的狀態服從:x_k\sim N({{\bar x}_k},{P_k})
我們希望得到狀態變量x 的最大後驗估計(MAP,Maximize a Posterior),於是計算:
\[\begin{array}{ccl} \hat x &=& \arg \mathop {\max }\limits_x p\left( {x|y,u} \right)\\ &=& \arg \max \frac{{p\left( {y|x,u} \right)p\left( {x|u} \right)}}{{p\left( {y|v} \right)}} \\ &=& \arg \max p(y|x)p\left( {x|u} \right) \end{array}\]
第二行是貝葉斯法則,第三行分母和x 無關所以去掉。
第一項即觀測方程式,有:\[p\left( {y|x} \right) = \prod\limits_{k = 0}^K {p\left( {{y_k}|{x_k}} \right)} \] ,很簡單。
第二項即運動方程式,有:\[p\left( {x|v} \right) = \prod\limits_{k = 0}^K {p\left( {{x_k}|{x_{k - 1}},v_k} \right)} \] ,也很簡單。
現在的問題是如何求解這個最大化問題。對於高斯分布,最大化問題可以變成最小化它的負對數。當我對一個高斯分布取負對數時,它的指數項變成了一個二次項,而前面的因子則變為一個無關的常數項,可以略掉(這部份我不敲了,有疑問的同學可以問)。於是,定義以下形式的最小化函式:
\[\begin{array}{l} {J_{y,k}}\left( x \right) = \frac{1}{2}{\left( {{y_k} - {C_k}{x_k}} \right)^T}R_k^{ - 1}\left( {{y_k} - {C_k}{x_k}} \right)\\ {J_{v,k}}\left( x \right) = \frac{1}{2}{\left( {{x_k} - {A_{k - 1}}{x_{k - 1}} - {v_k}} \right)^T}Q_k^{ - 1}\left( {{x_k} - {A_{k - 1}}{x_{k - 1}} - {v_k}} \right) \end{array}\]
那麽最大後驗估計就等價於:
\[\hat x = \arg \min \sum\limits_{k = 0}^K {{J_{y,k}} + {J_{v,k}}} \]
這個問題現在是二次項和的形式,寫成矩陣形式會更加清晰。定義:
\[\begin{array}{l} z = \left[ \begin{array}{l} {x_0}\\ {v_1}\\ \vdots \\ {v_K}\\ {y_0}\\ \vdots \\ {y_K} \end{array} \right],x = \left[ \begin{array}{l} {x_0}\\ \vdots \\ {x_K} \end{array} \right]\\ H = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}\\ { - {A_0}}&1&{}&{}\\ {}& \ddots & \ddots &{}\\ {}&{}&{ - {A_{K - 1}}}&1\\ {{C_0}}&{}&{}&{}\\ {}& \ddots &{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{C_K}} \end{array}} \right],W = \left[ {\begin{array}{*{20}{c}} {{P_0}}&{}&{}&{}&{}&{}&{}\\ {}&{{Q_1}}&{}&{}&{}&{}&{}\\ {}&{}& \ddots &{}&{}&{}&{}\\ {}&{}&{}&{{Q_K}}&{}&{}&{}\\ {}&{}&{}&{}&{{R_1}}&{}&{}\\ {}&{}&{}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{}&{}&{{R_K}} \end{array}} \right] \end{array}\]
就得到矩陣形式的,類似最小平方的問題:
\[J\left( x \right) = \frac{1}{2}{\left( {z - Hx} \right)^T}{W^{ - 1}}\left( {z - Hx} \right)\]
於是令它的導數為零,得到:
\[\frac{{\partial J}}{{\partial {x^T}}} = - {H^T}{W^{ - 1}}\left( {z - Hx} \right) = 0 \Rightarrow \left( {{H^T}{W^{ - 1}}H} \right)x = {H^T}{W^{ - 1}}z\] (*)
讀者會問,這個問題和卡爾曼濾波有什麽問題呢?事實上, 卡爾曼濾波就是遞推地求解(*)式的過程 。所謂遞推,就是只用x_{k-1} 來計算x_k 。對(*)進行Cholesky分解,就可以推出卡爾曼濾波器。詳細過程限於篇幅就不推了,把卡爾曼的結論寫一下:
\[\begin{array}{l} {{\tilde P}_k} = {A_{k - 1}}{{\hat P}_{k - 1}}A_{k - 1}^T + {Q_k}\\ {{\tilde x}_k} = {A_{k - 1}}{{\hat x}_{k - 1}} + {v_k}\\ {K_k} = {{\tilde P}_k}C_k^T{\left( {{C_k}{{\tilde P}_k}C_k^T + {R_k}} \right)^{ - 1}}\\ {{\hat P}_k} = \left( {I - {K_k}{C_k}} \right){{\tilde P}_k}\\ {{\hat x}_k} = {{\tilde x}_k} + {K_k}\left( {{y_k} - {C_k}{{\tilde x}_k}} \right) \end{array}\]
前兩個是預測,第三個是卡爾曼增益,四五是校正。
另一方面,能否直接求解(*)式,得到\hat{x} 呢?答案是可以的,而且這就是最佳化方法(batch optimization)的思路:將所有的狀態放在一個向量裏,進行求解。與卡爾曼濾波不同的是,在估計前面時刻的狀態(如x_1 )時,會用到後面時刻的資訊(y_2,y_3 等)。從這點來說,最佳化方法和卡爾曼處理資訊的方式是相當不同的。
================== 擴充套件卡爾曼濾波器 ===================
線性高斯系統當然性質很好啦,但許多現實世界中的系統都不是線性的,狀態和雜訊也不是高斯分布的。例如上面舉的雷射觀測方程式就不是線性的。當系統為非線性的時候,會發生什麽呢?
一件悲劇的事情是: 高斯分布經過非線性變換後,不再是高斯分布。而且,是個什麽分布,基本說不上來 。(攤手)
如果沒有高斯分布,上面說的那些都不再成立了。 於是EKF說,嘛,我們睜一只眼閉一只眼,用高斯分布去近似它,並且,在工作點附近對系統進行線性化 。當然這個近似是很成問題的,有什麽問題我們之後再說。
EKF的做法主要有兩點。其一,在工作點附近\[{{\hat x}_{k - 1}},{{\tilde x}_k}\] ,對系統進行線性近似化:
\[\begin{array}{l} f\left( {{x_{k - 1}},{v_k},{w_k}} \right) \approx f\left( {{{\hat x}_{k - 1}},{v_k},0} \right) + \frac{{\partial f}}{{\partial {x_{k - 1}}}}\left( {{x_{k - 1}} - {{\hat x}_{k - 1}}} \right) + \frac{{\partial f}}{{\partial {w_k}}}{w_k}\\ g\left( {{x_k},{n_k}} \right) \approx g\left( {{{\tilde x}_k},0} \right) + \frac{{\partial g}}{{\partial {x_k}}}{n_k} \end{array}\]
這裏的幾個偏導數,都在工作點處取值。於是呢,它就被 活生生地當成了一個線性系統 。
第二,線上性系統近似下,把雜訊項和狀態都 當成了高斯分布 。這樣,只要估計它們的均值和共變異數矩陣,就可以描述狀態了。經過這樣的近似之後呢,後續工作都和卡爾曼濾波是一樣的了。所以EKF是卡爾曼濾波在NLNG系統下的直接擴充套件(所以叫擴充套件卡爾曼嘛)。EKF給出的公式和卡爾曼是一致的,用線性化之後的矩陣去代替卡爾曼濾波器裏的轉移矩陣和觀測矩陣即可。
\[\begin{array}{l} {{\tilde P}_k} = {F_{k - 1}}{{\hat P}_{k - 1}}F_{k - 1}^T + Q_k'\\ {{\tilde x}_k} = f\left( {{{\hat x}_{k - 1}},{v_k},0} \right)\\ {K_k} = {{\tilde P}_k}G_k^T{\left( {{G_k}{{\tilde P}_k}G_k^T + R_k'} \right)^{ - 1}}\\ {{\hat P}_k} = \left( {I - {K_k}{G_k}} \right){{\tilde P}_k}\\ {{\hat x}_k} = {{\tilde x}_k} + {K_k}\left( {{y_k} - g({{\tilde x}_k},0)} \right) \end{array}\] 其中\[F_{k-1} = {\left. {\frac{{\partial f}}{{\partial {x_{k - 1}}}}} \right|_{{{\hat x}_{k - 1}}}},{G_k} = {\left. {\frac{{\partial g}}{{\partial {x_k}}}} \right|_{{{\tilde x}_k}}}\]
這樣做聽起來還是挺有道理的,實際上也是能用的,但是問題還是很多的。
考慮一個服從高斯分布的變量x \sim N(0,1) ,現在y=x^2 ,問y 服從什麽分布?
我機率比較差,不過這個似乎是叫做卡爾方布。y 應該是下圖中k=1那條線。
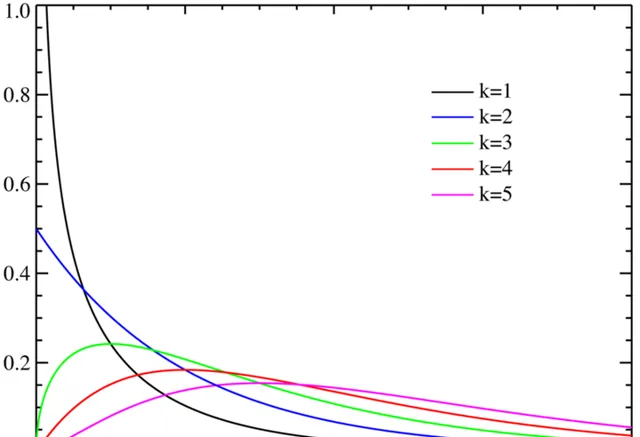
但是按照EKF的觀點,我們要用一個高斯分布去近似y 。假設我們采樣時得到了一個x=0.5 ,那麽就會近似成一個均值為0.25的高斯分布,然而卡方分布的期望應該是1。……但是各位真覺得k=1那條線像哪個高斯分布嗎?
所以EKF面臨的一個重要問題是,當一個高斯分布經過非線性變換後,如何用另一個高斯分布近似它?按照它現在的做法,存在以下的局限性:(註意是濾波器自己的局限性,還沒談在SLAM問題裏的局限性)。
- 即使是高斯分布,經過一個非線性變換後也不是高斯分布。EKF只計算均值與共變異數,是在用高斯近似這個非線性變換後的結果。(實際中這個近似可能很差)。
- 系統本身線性化過程中,丟掉了高階項。
- 線性化的工作點往往不是輸入狀態真實的均值,而是一個估計的均值。於是,在這個工作點下計算的F,G ,也不是最好的。
- 在估計非線性輸出的均值時,EKF算的是\mu_y=f(\mu_x) 的形式。這個結果幾乎不會是輸出分布的真正期望值。共變異數也是同理。
那麽,怎麽克服以上的缺點呢?途徑很多,主要看我們想不想維持EKF的假設。如果我們比較乖,希望維持高斯分布假設,可以這樣子改:
- 為了克服第3條工作點的問題,我們以EKF估計的結果為工作點,重新計算一遍EKF,直到這個工作點變化夠小。是為叠代EKF(Iterated EKF, IEKF)。
- 為了克服第4條,我們除了計算\mu_y=f(\mu_x) ,再計算其他幾個精心挑選的采樣點,然後用這幾個點估計輸出的高斯分布。是為Sigma Point KF(SPKF,或UKF)。
如果不那麽乖,可以說: 我們不要高斯分布假設,憑什麽要用高斯去近似一個長得根本不高斯的分布呢? 於是問題變為,丟掉高斯假設後,怎麽描述輸出函式的分布就成了一個問題。一種比較暴力的方式是:用足夠多的采樣點,來表達輸出的分布。這種蒙地卡羅的方式,也就是粒子濾波的思路。
如果再進一步,可以丟棄濾波器思路,說: 為什麽要用前一個時刻的值來估計下一個時刻呢 ? 我們可以把所有狀態看成變量,把運動方程式和觀測方程式看成變量間的約束,構造誤差函式,然後最小化這個誤差的二次型。 這樣就會得到非線性最佳化的方法,在SLAM裏就走向圖最佳化那條路上去了。不過,非線性最佳化也需要對誤差函式不斷地求梯度,並根據梯度方向叠代,因而局部線性化是不可避免的。
可以看到,在這個過程中,我們逐漸放寬了假設。
============== UKF 無跡卡爾曼 ==================
由於題主問題裏沒談IEKF,我們就簡單說說UKF和PF。
UKF主要解決一個高斯分布經過非線性變換後,怎麽用另一個高斯分布近似它。假設x \sim N(\mu_x \Sigma_{xx} ), y=g(x) ,我們希望用N(\mu_y, \Sigma_{yy}) 近似y 。按照EKF,需要對g 做線性化。但在UKF裏,不必做這個線性化。
UKF的做法是找一些叫做Sigma Point的點,把這些點用g 投影過去。然後,用投影之後的點做出一個高斯分布,如下圖:
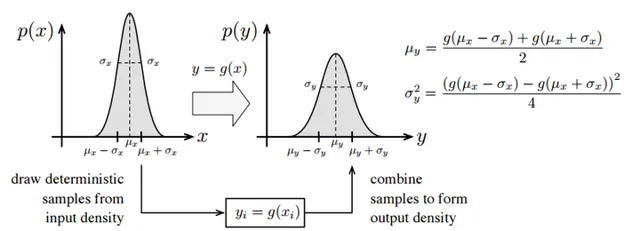
這裏選了三個點:\mu_x, \mu_x+\sigma_x, \mu_x-\sigma_x 。對於維數為N的分布,需要選2N+1個點。篇幅所限,這裏就不解釋這些點怎麽選,以及為何要這樣選了。總之UKF的好處就是:
=============== PF 粒子濾波 ==================
UKF的一個問題是輸出仍假設成高斯分布。然而,即使在很簡單的情況下,高斯的非線性變換仍然不是高斯。並且,僅在很少的情況下,輸出的分布有個名字(比如卡方),多數時候你都不知道他們是啥……更別提描述它們了。
因為描述很困難,所以粒子濾波器采用了一種暴力的,用大量采樣點去描述這個分布的方法(老子就是無參的你來打我呀)。框架大概像下面這個樣子,就是一個不斷采樣——算權重——重采樣的過程:
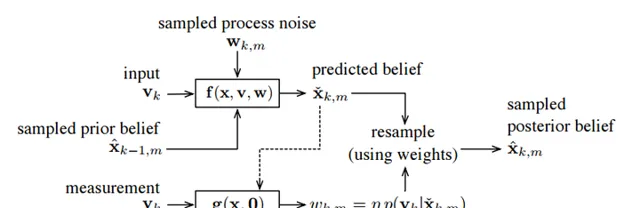
越符合觀測的粒子擁有越大的權重,而權重越大就越容易在重采樣時被采到。當然,每次采樣數量、權重的計算策略,則是粒子濾波器裏幾個比較麻煩的問題,這裏就不細講了。
這種采樣思路的最大問題是: 采樣所需的粒子數量,隨分布是指數增長的 。所以僅限於低維的問題,高維的基本就沒辦法了。
=============== 非線性最佳化 ==================
非線性最佳化,計算的也是最大後驗機率估計(MAP),但它的處理方式與濾波器不同。對於上面寫的狀態估計問題,可以簡單地構造誤差項:
\[\begin{array}{l} {e_{v,k}}\left( x \right) = {x_k} - f\left( {{x_{k - 1}},{v_k},0} \right)\\ {e_{y,k}}\left( x \right) = {y_k} - g\left( {{x_k},0} \right) \end{array}\]
然後最小化這些誤差項的二次型:
\[\min J\left( x \right) = \sum\limits_{k = 1}^K {\left( {\frac{1}{2}{e_{v,k}}{{\left( x \right)}^T}W_{v,k}^{ - 1}{e_{v,k}}\left( x \right)} \right) + \sum\limits_{k = 1}^K {\left( {\frac{1}{2}{e_{y,k}}{{\left( x \right)}^T}W_{v,k}^{ - 1}{e_{v,k}}\left( x \right)} \right)} } \]
這裏僅用到了雜訊項滿足高斯分布的假設,再沒有更多的了。當構建一個非線性最佳化問題之後,就可以從一個初始值出發,計算梯度(或二階梯度),最佳化這個目標函式。常見的梯度下降策略有牛頓法、高斯-牛頓法、Levenberg-Marquardt方法,可以在許多講數值最佳化的書裏找到。
非線性最佳化方法現在已經成為視覺SLAM裏的主流,尤其是在它的稀疏性質被人發現且利用起來之後。它與濾波器最大不同點在於, 一次可以考慮整條軌跡中的約束。它的線性化,即亞可比矩陣的計算,也是相對於整條軌跡的。相比之下,濾波器還是停留在馬可夫的假設之下,只用上一次估計的狀態計算當前的狀態。可以用一個圖來表達它們之間的關系:

當然最佳化方式也存在它的問題。例如最佳化時間會隨著節點數量增長——所以有人會提double window optimization這樣的方式,以及可能落入局部極小。但是就目前而言,它比EKF還是優不少的。
=============== 小結 ==================
- 卡爾曼濾波是遞迴的線性高斯系統最優估計。
- EKF將NLNG系統在工作點附近近似為LG進行處理。
- IEKF對工作點進行叠代。
- UKF沒有線性化近似,而是把sigma point進行非線性變換後再用高斯近似。
- PF去掉高斯假設,以粒子作為采樣點來描述分布。
- 最佳化方式同時考慮所有幀間約束,叠代線性化求解。
呃好像題主還問了FastSLAM,有空再寫吧……
註:
* 本文大量觀點來自Timothy. Barfoot, "State estimation for Robotics: A Matrix Lei Group Approach", 2016. 圖片若有侵權望告知。








