這篇回答節選自我的專欄 【機器學習中的數學:機率圖與隨機過程】 ,我們來仔細介紹和分析一下粒子濾波。
也歡迎關註我的知乎帳號 @石溪 ,將持續釋出機器學習數學基礎及演算法套用等方面的精彩內容。
我們知道,卡爾曼濾波是可以得到解析解的,而原因是 z_t 和 z_{t-1} 之間是線性關系,且變量服從高斯分布。我們回想一下,正式因為高斯分布的完美特性,導致了我們可以拿出濾波結果的解析解。
但是這畢竟是一種非常特殊的情況,換句話說,如果在更一般的情況下 z_t 和 z_{t-1} 之間不滿足線性關系,而是可以滿足任意關系,且變量不服從高斯分布,那麽會是什麽樣的一種情形?這就是我們這裏要介紹的粒子濾波。
粒子濾波中,我們同樣最關系的也是濾波問題(filtering):即關註 p(z_t|x_1,x_2,...,x_t) 的機率分布,我們回憶一下分兩步:
第一步: predict 。從貝葉斯的角度來說,實際上就是利用上一步 t-1 步的濾波值,先估計出一個 z_t 的先驗機率:
p(z_t|x_1,...,x_{t-1})=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_1,...,x_{t-1})dz_{t-1}
第二步: update 。在拿到 t 時刻的觀測變量 x_t ,我們稱之為證據之後,對上一步得到的 z_t 先驗機率分布進行修正,得到我們要的濾波,本質上就是去求得 z_t 的後驗分布:
p(z_t|x_1,...,x_t)\propto p(x_t|z_t)p(z_t|x_1,...,x_{t-1})
此時的我們,無法擁有高斯分布和線性關系這麽完美的假設,因此不再能夠像卡爾曼濾波那樣得到濾波的解析解,怎麽辦?我們想到了之前學習過的蒙地卡羅方法,得不到解析解,我們去求數值解。
具體怎麽弄,我們看一下重要性采樣方法:
這裏我們要樹立一個觀點,我們在 predict 和 update 兩步的不斷叠代過程中,都是在想著不斷的求得 z 的機率分布,實際上分布並不是我們最終需要的結果,有了分布後,我們最終還要做一步就是,取分布中最大機率密度的那個 z 值作為我們的估計。
因此,數值解的方法,就是直接面向最終的估計值,如果說 z_t 服從機率分布 p(z_t|x_1,...,x_t) ,那麽數值解方法的最終目標就是求得變量 z_t 的期望,來作為 t 時刻這一步濾波的估計值。那麽每一步同樣都能獲得濾波結果。
具體怎麽做,首先第一個要用到的思想就是重要性采樣方法:
假如變量 z 服從分布 p(z) ,如何求得 z 的期望?
按照連續型隨機變量期望的定義: E[z]=\int zp(z)dz ,進一步如果依據大數定理,依據采樣的方法從分布 p(z) 中采出 N 個樣本 z_i ,求他們的算術平均,同樣可以作為期望的近似,這個我們在機率統計基礎中已經多次講過:
E[z]=\int zp(z)dz \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}
其中, z^{(i)} 就是從分布 p(z) 中采樣出來的 N 個樣本,但是問題來了,如何從 p(z) 中生成樣本 z^{(i)} ,這個我們並不知道啊,換句話說 p(z) 是一個復雜的分布,我們沒辦法從中采到服從分布的樣本。
重要性采樣就呼之欲出了,他在求期望的過程中引入了一個建議分布 q(z) ,這個建議分布可以是一個任意的我們熟悉的分布,他可以使得我們可以輕松的從 q(z) 中生成服從 q(z) 分布的一系列樣本。
那這個建議分布 q(z) 有啥用呢?還是回到期望的定義式中:
E[z]=\int zp(z)dz=\int z\frac{p(z)}{q(z)}q(z)dz
經過這麽一個漂亮的變形,我們發現,隨機變量 z 的期望就可以變成下面這種形式:
E[z]=\int z\frac{p(z)}{q(z)}q(z)dz \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}\frac{p(z^{(i)})}{q(z^{(i)})}
這時,這一組 N 個生成的樣本 z^{(i)} 就不再是從分布$p(z)$中生成的了,而是從 q(z) 中生成的, q(z) 是我們指定的建議分布,因此用它來生成一組樣本,我們還是辦得到的
這個過程中 \frac{p(z^{(i)})}{q(z^{(i)}} 就稱為樣本 z^{(i)} 的權重,記作 w^{(i)} ,既有:
E[z] \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}\frac{p(z^{(i)})}{q(z^{(i)})}=\frac{1}{N}\sum_{i=1}^Nz^{(i)} w^{(i)}
好,回到粒子濾波的問題中來,我們的問題也是類似的:
在 t 時刻,我們用數值解求濾波的近似結果,實際上就是求服從分布 p(z_t|x_{1:t}) 的變量 z 的期望。那麽套用重要性采樣方法,我們引入建議分布 q(z_t|x_{1:t}) ,那麽每一輪過程中,比如在 t 時刻:
我們用建議分布 q(z_t|x_{1:t}) 生成 N 個樣本:
z_t^{(1)},z_t^{(2)},z_t^{(3)},...,z_t^{(N)}
然後再用權重公式公式 w_t^{(i)}=\frac{p(z_t^{(i)}|x_{1:t})}{q(z_t^{(i)}|x_{1:t})}
來對應的生成樣本 z_t^{(1)},z_t^{(2)},z_t^{(3)},...,z_t^{(N)} 所對應權重 w_t^{(1)},w_t^{(2)},w_t^{(3)},...,w_t^{(N)} ,然後透過 \frac{1}{N}\sum_{i=1}^Nz^{(i)} w^{(i)} 來求得這一輪濾波值的期望。
但是問題來了,不像單純的重要性采樣中的情形,在上面的重要性采樣的例子當中,我們雖然不能從 p(z) 中生成樣本,但是畢竟我們知道 p(z) 的解析式,可以求得 p(z) 的值,但是粒子濾波中的時間 t 中, p(z_t^{(i)}|x_{1:t}) 我們也求不出來,只有當 t=1 時, p(z_1^{(i)}|x_1) 可以透過 p(z_1^{(i)}|x_1) \propto p(z_1^{(i)})p(x_1|z_1^{(i)}) 獲得,
到了這兒,思路就明確了,怎麽求?用遞推,每一輪我們都的采樣 N 個樣本 z
那麽在 t-1 時刻, N 個樣本 z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} 所對應的權重為 w_{t-1}^{(1)},w_{t-1}^{(2)},w_{t-1}^{(3)},...,w_{t-1}^{(N)}
而在 t 時刻 N 個樣本 z_{t}^{(1)},z_{t}^{(2)},z_{t}^{(3)},...,z_{t}^{(N)} 所對應的權重為 w_{t}^{(1)},w_{t}^{(2)},w_{t}^{(3)},...,w_{t}^{(N)}
那麽我們只要試圖去求得兩個對應位置上的樣本 z_{t-1}^{(i)} 和$z_{t}^{(i)}$他們二者權重之間的遞迴關係,也就是 w_{t-1}^{(i)} 和 w_{t}^{(i)} ,從 t=1 開始,一步一步的采樣 z_t^{(i)} ,一輪一輪的叠代出 w_{t}^{(i)} ,就能成功的實作濾波的目標。
下面我們來看具體如何求解
這裏為了簡化計算,用得是 p(z_{1:t}|x_{1:t}) 這個機率,這是一種簡化運算的假設,大家註意這點就好,那麽權重的運算式就表示為:w_t=\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}
我們看看如何化簡這個運算式,首先看分子
p(z_{1:t}|x_{1:t})=\frac{p(z_{1:t},x_{1:t})}{p(x_{1:t})}=\frac{1}{C}p(z_{1:t},x_{1:t})
這裏是因為 p(x_{1:t}) 是觀測變量 x_{1:t} 的機率,很顯然可以記作常數 C ,接著
p(z_{1:t}|x_{1:t})=\frac{1}{C}p(z_{1:t},x_{1:t})=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_{1:t},x_{1:t-1})\\=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_t|z_{1:t-1},x_{1:t-1})p(z_{1:t-1},x_{1:t-1})\\=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_t|z_{1:t-1},x_{1:t-1})p(z_{1:t-1}|x_{1:t-1})p(x_{1:t-1})
這裏由觀測獨立性假設有: p(x_t|z_{1:t},x_{1:t-1})=p(x_t|z_t)
由齊次馬爾科夫假設有: p(z_t|z_{1:t-1},x_{1:t-1})=p(z_t|z_{t-1})
同時, p(x_{1:t-1}) 也是一組觀測變量的機率,記作常數 D 。
最終化簡為:
p(z_{1:t}|x_{1:t})=\frac{D}{C}p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1})
再看看分母 q 分布該如何化簡,先按條件機率公式轉化一下,
q(z_{1:t}|x_{1:t})=q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t})
然後這裏有一個小技巧,那就是時刻 t 以前的隱含變量的取值顯然不受 t 時刻觀測變量 x_t 取值的影響,因此就有:
q(z_{1:t-1}|x_{1:t})=q(z_{1:t-1}|x_{1:t-1})
那麽:
q(z_{1:t}|x_{1:t})=q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1})
那麽此時我們權重 w_t 的運算式就能夠完整的寫出來了:
w_t=\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1})}{q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1})}
我們欣喜的發現,等式的最後一部份就是 w_{t-1} 的運算式: \frac{p(z_{1:t-1}|x_{1:t-1})}{q(z_{1:t-1}|x_{1:t-1})}=w_{t-1}
w_t\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}
而此時我們還需要補充一點的就是,由於 q 分布是我們的提議分布,意味著我們可以選擇任意我們覺得方便的分布,那麽我們讓分布 q 取如下形式:
q(z_t|z_{1:t-1},x_{1:t})=p(z_t|z_{t-1})
最後一步轉化是因為齊次馬爾科夫性質決定的,那麽 w_t 的遞迴關係就瞬間簡單了:
w_t\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}=\frac{p(x_t|z_t)p(z_t|z_{t-1})}{p(z_t|z_{t-1})}w_{t-1}=p(x_t |z_t)w_{t-1}
\Rightarrow w_t\propto p(x_t |z_t)w_{t-1}
而由於我們所有粒子 z^{(i)} 所對應的權重 w_t^{(i)} 最終要透過歸一化處理使得他們的和為 1 ,因此這裏的正比可以直接處理為相等,反正最終還要歸一化的嘛:
\Rightarrow w_t=p(x_t|z_t)w_{t-1}
而我們發現 p(x_t|z_t) 反映的是 t 時刻隱變量 z_t 到觀測變量 x_t 之間的轉移機率,這個是模型已知的,由此 t 時刻和 t-1 時刻的權重遞迴關係就出來了。
有了這個遞迴關係,具體應該如何進行濾波的過程,我們在下一講中詳細介紹。
在上一講中,我們已經得到了 t-1 時刻和 t 時刻權重之間的關系: w_t= p(x_t|z_t)w_{t-1} ,那麽粒子濾波中的采樣過程具體就描述如下,顯然這是一個叠代的過程:
前提:在 t-1 時刻采樣過程已完成
那麽在 t 時刻,我們采樣 N 個 z_t^{(i)} 個樣本點
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim q(z_t|z_{t-1}^{(i)},x_{1:t})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}\frac{p(x_t|z_t^{(i)})p(z_t^{(i)}|z_{t-1}^{(i)})}{q(z_t^{(i)}|z_{t-1}^{(i)},x_{1:t})}
end:\,\,w_t^{(i)} 進行歸一化,使得 \sum_1^{N}w_t^{(i)}=1
由於我們選擇了提議分布 q : q(z_t^{(i)}|z_{t-1}^{(i)},x_{1:t})=p(z_t^{(i)}|z_{t-1}^{(i)}) ,則這個采樣和權值叠代的過程就進一步簡化為了:
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)})
end:\,\,w_t^{(i)} 進行歸一化,使得 \sum_1^{N}w_t^{(i)}=1
我簡要的解讀一下這個過程,實際上在時間 t 時刻,我們需要從分布 p(z_t|z_{t-1}^{(i)}) 中采樣 N 個樣本 z_t^{(i)} ,同時我們在上一步 t-1 時刻曾經也得到了一輪采樣樣本 z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} ,其中每一個采樣樣本 z_{t-1}^{(i)} 對應的權重就是 w_{t-1}^{(i)} 。那麽在時刻 t 的這一輪采樣過程中,我們對於每一個采樣樣本 z_t^{(i)} ,僅僅透過 w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 的叠代計算,我們就能獲得該樣本點 z_{t}^{(i)} 的權重 w_t^{(i)} 。
那麽每一輪的權重都可以透過這種方法獲得,至於說初始時刻的 w_1^{(i)} 如何獲取,
當 t=1 時,帶入有 w_1^{(t)}= w_{0}^{(i)}p(x_1|z_1^{(i)}) ,由於並沒有 t=0 時刻,因此所有的 0 時刻權重 w_0^{(i)} 都處理為 1 。同時 t=1 時, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 中的 p(z_t|z_{t-1}^{(i)}) 也直接就是初始機率分布 p(z_1)
那麽我們把 t=1 時刻的情況帶入,合並成完整的粒子濾波流程:
t=1:
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_1^{(i)}\sim p(z_1)
\,\,\,\,\,\, w_1^{(t)}= p(x_1|z_1^{(i)})
w_1^{(i)} 進行歸一化,使得 \sum_1^{N}w_1^{(i)}=1
t\ge 2: 開始迴圈
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)})
end:\,\,w_t^{(i)} 進行歸一化,使得 \sum_1^{N}w_t^{(i)}=1
這裏有一個點需要提醒一下大家:
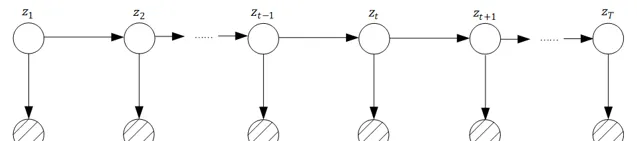
初始機率 p(z_1) ,狀態轉移機率 p(z_t|z_{t-1}) 和發射機率$p(x_t|z_t)$,這三種機率在隱馬可夫模型、卡爾曼濾波和粒子濾波中都有,但是他們的表現形式不同,我們總結回顧一下:
對於隱馬可夫模型,初始機率 p(z_1) 取自於機率向量 \pi ,而狀態轉移機率 p(z_t|z_{t-1}) 和發射機率 p(x_t|z_t) 取自於狀態轉移機率矩陣 A 和發射機率矩陣 B 中的對應項
對於卡爾曼濾波,三個機率都必須服從高斯分布: p(z_t|z_{t-1})=N(Az_{t-1}+B,Q) 和 p(x_t|z_t)=N(Cz_t+D,R),p(z_1)=N(\mu_1,\sigma_1)
而粒子濾波則沒有任何約束,三個機率都可定義為任意函式形式:
p(z_t|z_{t-1})=f(z_{t-1}) 、 p(x_t|z_t)=g(x_t),p(z_1)=f_0(z_1)
那麽我們從比較卡爾曼濾波和粒子濾波的角度來看看,從時間 t-1 時刻到 t 時刻的叠代本質到底是什麽,先看看卡爾曼濾波,卡爾曼濾波關於隱變量 z_t 的估計,實際上是一個高斯分布:
我們知道,在 t-1 時刻,我們透過 predict 步驟,得到了一個預測機率
p(z_t|x_1,x_2,x_3,...,x_{t-1})\\=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_1,x_2,x_3,...,x_{t-1})dz_{t-1}
這本質上是先拿到了隱變量 z_t 的一個先驗高斯分布,然後我們在 t 時刻的 update 步驟,是我們觀察到 t 時刻的觀測變量 x_t ,對先驗高斯分布進行修正,得到後驗分布,也就是濾波的結果:
p(z_t|x_1,x_2,x_3,...,x_t)\propto p(x_t|z_t)p(z_t|x_1,x_2,x_3,...,x_{t-1})
簡單點說,從 t-1 時刻的 predict 步驟到 t 時刻的 update 步驟,就是從一個高斯分布變化到另一個高斯分布的過程,高斯分布僅由均值和變異數決定,因此前後需要發生改變的就是均值和變異數,如下圖所示:
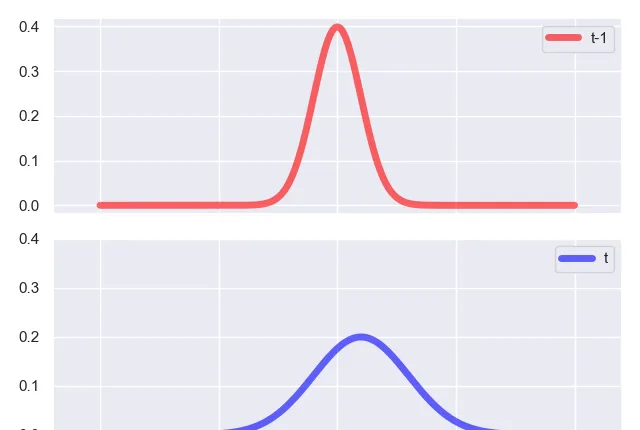
而粒子濾波呢?因為沒有高斯分布這麽好的解析形式,我們沒辦法在每一輪叠代的過程中獲得他的分布的解析形式,因此我們采用蒙地卡羅方法進行采樣,用數值的方法進行采樣,換句話說,就是在 t-1 時刻,我們獲得了 N 個采樣的樣本: z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} ,對應了各自不同的權重 w_{t-1}^{(1)},w_{t-1}^{(2)},w_{t-1}^{(3)},...,w_{t-1}^{(N)} ,這實際上就是一個分布列,這個分布列近似的表示了 z_t 的後驗分布,而我們正是透過這個分布列求得期望,作為這一輪濾波的估計值,而到了 t 時刻,我們透過 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 和 w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 來獲取新的 t 時刻的分布列的值和各自對應的權重。可以說如果我們明確了概念,即離散型的隨機變量的分布列就是連續型隨機變量機率分布的一種近似的話,那麽粒子濾波從 t-1 時刻到 t 時刻也是從一個分布到另一個分布的變化過程,這裏變的更本質,變得就是所有隨機變量 (z_t^{(i)}) 的取值和對應的權重,回憶一下,分布列的兩要素不就是隨機變量的取值和他們各自所對應的權重嗎?這麽一想就非常清晰了。
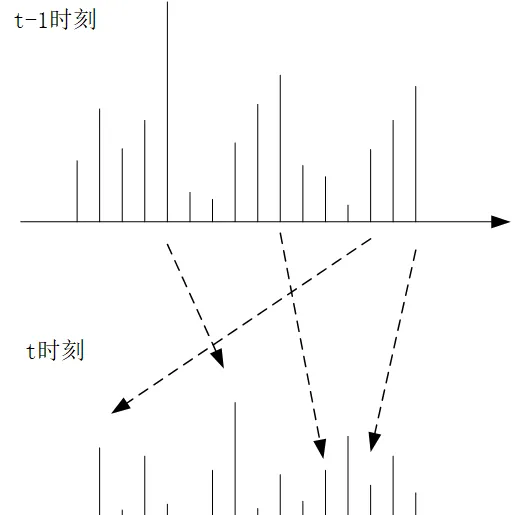
從圖中我們可以清晰的看出粒子濾波叠代的本質,從 t-1 時刻到 t 時刻,虛線箭頭表面,每一個采樣點 z^{(i)} 的取值發生了變化,權重也發生了變化。
似乎,粒子濾波就應該介紹完了,但是在最後我想提一個問題,也就是權值衰退的問題,一般例子濾波在經過叠代幾輪後,很可能在他的分布列中,某一個取值的權重很大,而其他的都很小,如下圖所示:
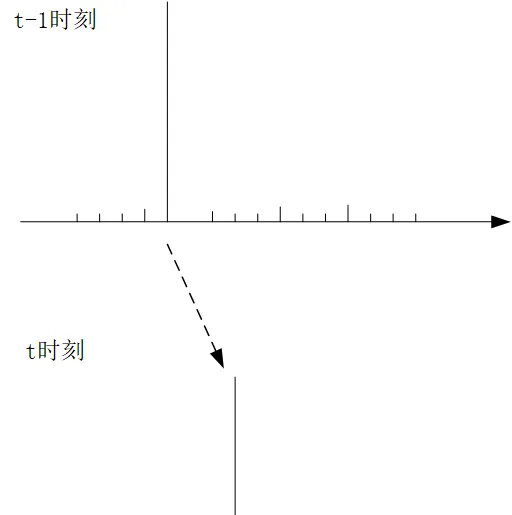
也就是當某一個采樣點的權重非常大,其他的采樣點非常小的情況下,後續叠代都會保持這種趨勢,而導致各個采樣點的權值出現了衰退,首先這種情況是沒有意義的,這種一枝獨秀的情況,這就不能很好的反映這些采樣點整體的分布了,或者說他可能都不叫分布了。
在考慮如何了解決這種問題之前,我們先來想想為什麽會這樣,在前面講的粒子濾波演算法中,這 N 個樣本進行叠代的時候,每個樣本點都處理一次,這一次處理透過 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 確定 t 時刻這個采樣點的值,同時連帶的透過 w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 把權重也攜帶過去了。因此那個權重極大的采樣點,下一輪的權重依然非常大,而權重很小的(接近於 0 ),總體上看,下一輪權值依舊很小。概括成一句話就是:在 t-1 到 t 的叠代過程中, N 個樣本點,每個采樣點只處理一次,權重隨著值一起轉移了。
那麽從直覺上改變思路,應該讓采樣點的值轉移的過程和權重脫鉤,但又要反映各個采樣點的權重內容,這個既要、又要怎麽實作?這裏就要介紹重采樣的思路:
打個比方,考慮一種比較極端的情況,比如 z^{(j)}_{t-1} 的權重是0.85, z^{(k)}_{t-1} 的權重是0.1, z^{(m)}_{t-1} 的權重是0.05,其他采樣點的權重都為0了(當然實際情況應該是每個采樣點都有權重,這裏我們為了簡化描述,道理都是一樣的,請大家註意)。
那麽在$t-1$時刻到$t$時刻的采樣過程中,我們還是進行 N 次采樣,但是在每次采樣的過程中,我們讓其有0.85的機率去處理 z^{(j)}_{t-1} ,0.1的機率去處理 z^{(k)}_{t-1} ,0.05的機率去處理 z^{(m)}_{t-1} ,假設 N=100 ,那麽按照大數定理, z^{(j)}_{t-1} 的處理次數就是85次,這樣他同樣照顧到了 t-1 時刻各個采樣點的權重內容。但是他的好處卻很明顯,每一次都是依照 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 依照機率分布進行采樣確定下一輪的采樣值,顯然這85次依機率的采樣值的叠代結果 z_t^{(i)} 就不會集中於一點了
那權重如何處理呢?在 t-1 時刻,在 N 次采樣過程中,我們每一次所選中的采樣點,他的權重都是 \frac{1}{N} ,在這個例子中, N=100 ,每一次采樣的權重就是0.01,但是每次采樣有0.85的機率處理 z^{(j)}_{t-1} ,依照大數定理, z^{(j)}_{t-1} 的處理次數就是85次,仍然包含了原始采樣點的權重資訊,那麽叠代到下一輪 w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) ,決定了 t 時刻這個采樣點的權重,而且這裏面還蘊含了一個比較有意思的地方:
我們依照 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 機率取出了 t 時刻的樣本 z_t^{(i)} ,如果這個樣本對於生成觀測變量 x_t 是更加適合的,換句話說 p(x_t|z_t^{(i)}) 的值就更大,那麽這個樣本點在 t 時刻所對應的權重 w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) 就更大,這個道理和邏輯是很順的。
有一個圖做一個簡單圖示:
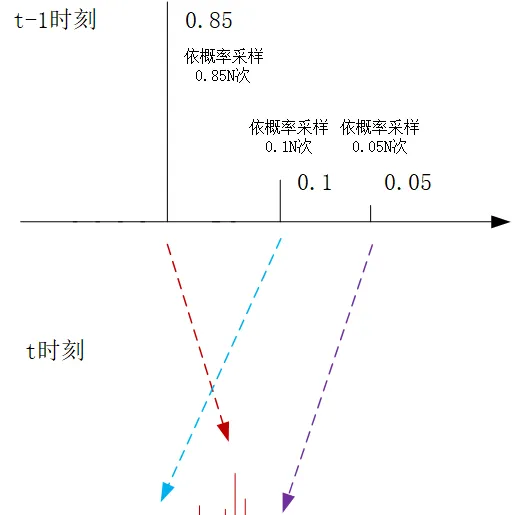
因此在前面基本的例子濾波叠代演算法的基礎上,我們在 t-1 輪生成了新的 N 個樣本點 z_{t-1}^{(i)} 以及他們的權重 w_{t-1}^{(i)} (這個稱之為更新前的權重)之後,在向 t 時刻的叠代過程中,我們的目標還是去采樣 N 個采樣點,我們首先更新 z_{t-1}^{(i)} 的權重,將他們都變成等權重的 \frac{1}{N} (這個稱之為更新後的權重),但是在每次采樣的過程中,我們依照更新前的權重 w_{t-1}^{(1)},w_{t-1}^{(2)},...,w_{t-1}^{(N)} ,依機率選擇一個采樣點進行處理,利用 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 獲得下一輪 t 時刻的新的采樣點的值,利用更新後的等權重值, w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) 得到這個采樣點在 t 時刻的權重。
這個就是加上重采樣最佳化後的粒子濾波的過程。至此,粒子濾波就介紹完了,的確比較復雜。
此內容節選自我的專欄【機器學習中的數學:機率圖與隨機過程】,前三節免費試讀,歡迎訂閱:
當然還有【機器學習中的數學(全集)】系列專欄,歡迎大家閱讀,配合食用,效果更佳~
有訂閱的問題可咨詢微信:zhangyumeng0422











