這個問題非常有意思,高贊答主們從各個角度描述了對數函式的定義及其導數,但是其核心問題還是沒有解決,即 對數函式 \ln x 為什麽在某些方面 像一個冪函式( x^0 ) 。
咋看之下這似乎是無稽之談,x^0 明明等於 1 ,而其它的冪函式的定義也跟對數函式全然不同,除了對數函式的導數也是冪函式之外,似乎就沒有其它相似之處了。
不過非常恰巧,我前段時間對各種不同的平均做了一點點研究,裏頭也有非常類似的「 對數函式表現的像一個冪函式 」的行為,不過讀者需要先花一點點時間了解一下什麽是 冪平均 。
對於兩個正實數 a 和 b ,我們知道他們的 算術平均 是 \frac{a+b}{2} , 幾何平均 是 \sqrt{ab} ,並且有算術幾何平均不等式: \frac{a+b}{2}\ge\sqrt{ab} ,這是中學數學的範疇。
到了大學之後,偶爾我們會遇到另一種平均值: 均方根 (root mean square, RMS),即\sqrt{\frac{a^2+b^2}{2}} ,不過理解這個平均值依然只需要中學數學知識就夠了:假設 a\le b (下同),不難發現 a=\sqrt{\frac{a^2+a^2}{2}}\le\sqrt{\frac{a^2+b^2}{2}}\le\sqrt{\frac{b^2+b^2}{2}}=b ,所以\sqrt{\frac{a^2+b^2}{2}} 確實介於a 和 b 之間,可以當作是某種平均值。
有了均方根,我們很容易就想到,如果把二次方改成三次方行不行?四次方、五次方呢?這就很容易匯出了 冪平均 的概念: M_n=\sqrt[n]{\frac{a^n+b^n}{2}} 。這樣一下子就把算術平均、均方根,推廣了無窮多種平均值,只要代入不同的 n 就可以了,比如 調和平均 就也被包含了進來: \frac{2}{\frac{1}{a}+\frac{1}{b}}=(\frac{a^{-1}+b^{-1}}{2})^{-1} 。
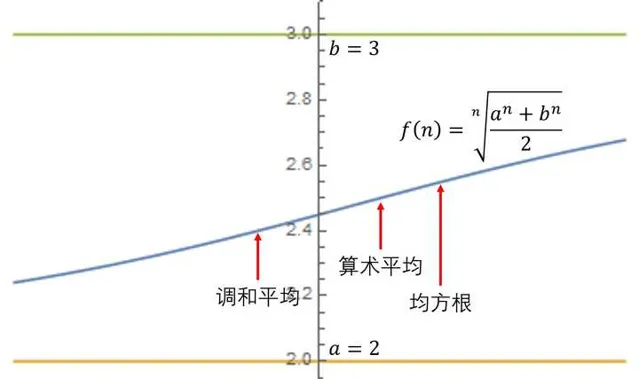
冪平均還有一個很有意思的性質,從圖上也可以看出來,就是它關於 n 是單調的。事實上,如果 n 趨向於正(負)無窮,那麽冪平均就會趨向於 b ( a )。對於任何有限的n ,則冪平均始終在 a 和 b 之間。
我們甚至可以對冪平均再做一次推廣,把冪函式換成任意函式,把求根換成該函式的逆函式,就得到 擬算術平均 (quasi-arithmetic mean),又叫 廣義f-平均 (generalized f-mean): M_f=f^{-1}(\frac{f(a)+f(b)}{2}) ,冪平均就對應於 f(x)=x^n 時的情形。
好了,現在背景知識都介紹完了,這與本來的問題有什麽關系呢?
別急,我們剛剛忘了提幾何平均了,既然冪平均可以一直從 a 走到 b ,那幾何平均在其中的什麽位置呢?
也許你已經猜到了,幾何平均就在 n=0 的位置!
註意到冪平均在 n=0 處是沒有定義的,因為不能開零次方根,但是我們可以用極限的角度定義 M_0=\lim_{n\rightarrow0}{M_n}=\sqrt{ab} 。
證明其實不難,只要註意到對於任意的 n>0 ,我們有 \sqrt[n]{\frac{a^n+b^n}{2}}\ge \sqrt[n]{\sqrt{a^nb^n}}=\sqrt{ab} ,而由於 x^{\frac1n} 當 n<0 時是單調減的所以不等號要反過來,就可以知道 \sqrt{ab} 只能在在 n=0 的位置了。
所以按照冪平均與 f(x)=x^n 的對應關系, \sqrt{ab} 似乎對應於f(x)=x^0 對應的廣義平均。然而事實上,\sqrt{ab}=\exp(\frac{\ln a+\ln b}2) 是f(x)=\ln x 下的廣義平均。這麽一看 \ln x 是不是跟冪函式 x^0 有了某些奇怪的相似關系了?
事實上,冪平均(包含 n=0 的特殊情形幾何平均)是唯一一種滿足 齊次性 的擬算術平均。什麽是齊次性呢?簡單地說, 2m (兩米)跟 3m 的平均值,根據平均值的定義方式的不同,不一定是 2.5m ,也許是比方說 2.3m 。但是如果我們把這兩個數換個單位,那麽齊次性要求 200cm 跟 300cm 在同一個定義下,平均值必須是 230cm 。換句話說, 我們要求平均值 M(a,b) 滿足M(200, 300)=100M(2,3) ,或者更一般的, M(\lambda a,\lambda b)=\lambda M(a,b) ,這就是(一次)齊次性。
這個齊次性的要求既自然又苛刻,事實上,只要我們要求廣義平均滿足齊次性,可以證明 f(x) 只能是冪函式 x^n 或者對數函式 \ln x ,頂多加上一個常數因子。其它的函式比如指數函式等都是不滿足這個性質的。
所以說,對數函式與冪函式的關系遠比表面上看起來更加復雜,其中更深入的關系還望有學數學的大神前來揭秘。
竟然這麽多人看,趁機推銷一下我自己寫的段子好了











