答案是肯定的! 美國著名的科普電視節目【流言終結者】中就曾做過摩托車能否滑水的測試實驗[1]。節目主持人傑米和亞當找來了摩托車特技選手來進行實驗,特技選手騎著摩托車從陸地加速駛入湖面,很輕松就穿過了 15 m 和 30 m 的湖面(圖 1)。高速攝影機顯示,摩托車確實是貼著水面行駛的。摩托車在穿越水面時,車輪有幾次彈跳現象。

由於太過好玩,節目主持人傑米也親自嘗試了一番,最終傑米駕著摩托車在水面上滑行了 100 多米才落入水中(圖 2)。

實驗已經證實:高速行駛的摩托車確實可以在水面行駛一段距離。但摩托車為什麽能在水面上行駛,摩托車在水面上是如何運動,如何才能在水面上行駛出更大的距離?本文將透過運動方程式的建立和數值求解,並結合因次分析來回答這些問題。
模型
摩托車之所以能在水面上行駛,其實原理和滑水運動中的滑板差不多。接下來本文先分析滑水運動中滑板的受力,然後在此基礎上再分析摩托車滑水時車輪的受力,並由受力分析匯出摩托車滑水的運動方程式。最後再透過因次分析嘗試尋找水面最大行駛距離與各參數的關系。
滑板模型
滑水運動和放風箏的原理類似[2,3],風箏能飛上天空是靠著風箏面有一個傾斜角度迎著風。這個適當的「迎風角」,使風力形成往上飛的升力。只不過光有風力還不夠,要想成功地讓風箏飛上天,還須要有拉風箏的線。只要接線的位置恰當,可以讓升力等於風箏本身的重力達到靜力平衡,風箏自然就能徜徉在藍天之中。
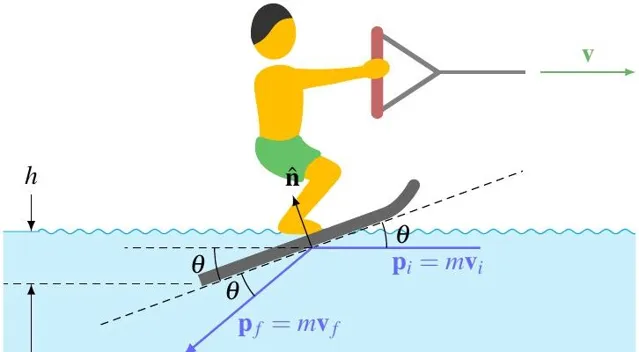
如圖 3 所示,滑水運動中滑水板與水面也有一個傾斜角度 \theta 。當滑板相對於水有一個速度 \mathbf{v} 時,大量水分子會以水平速度\mathbf{v}_i 撞擊滑板的下表面然後以速度 \mathbf{v}_f 反彈。為了簡單起見,假設這種碰撞是彈性的,即碰撞前後水分子相對滑板的速度大小相等。根據圖 3 可知
\mathbf{v}_i = -v\cdot \hat{\mathbf{x}},\quad \mathbf{v}_f = -v( \cos 2\theta \cdot \hat{\mathbf{x}}+ \sin 2\theta \cdot \hat{\mathbf{y}}) \\
其中 \hat{\mathbf{x}} 和 \hat{\mathbf{y}} 分別表示水平胡豎直方向上的單位向量。在時間間隔 \Delta t 內,與滑板下表面碰撞的水品質為
m = \rho w h v \Delta t \\
其中 \rho 為水的密度,h 為滑板浸入水中的深度,w 為滑板的寬度。因此,碰撞前後水動量的變化可表示為
\begin{aligned} \Delta \mathbf{p} &= m v (1- \cos 2\theta) \cdot \hat{\mathbf{x}} - mv \sin 2\theta \cdot \hat{\mathbf{y}}\\ & = \rho w h v^2 \Delta t (1- \cos 2\theta) \cdot \hat{\mathbf{x}} - \rho w h v^2 \Delta t \sin 2\theta \cdot \hat{\mathbf{y}} \end{aligned} \\
由動量定理可得滑板作用在水上的力為
\mathbf{F}_\mathrm{w} = \lim_{\Delta t\rightarrow 0} \frac{\Delta \mathbf{p}}{\Delta t} = \rho w h v^2 \big[(1-\cos 2\theta) \cdot \hat{\mathbf{x}} - \sin 2\theta \cdot \hat{\mathbf{y}}\big] \\
根據牛頓第三定律,水作用在滑板上的力與滑板作用在水上的力大小相等方向相反。因此,滑板受到水的作用力為
\mathbf{F}_\mathrm{s} = -\mathbf{F}_\mathrm{w} = \rho w h v^2 \big[(\cos 2\theta - 1) \cdot \hat{\mathbf{x}} + \sin 2\theta \cdot \hat{\mathbf{y}}\big] \\
該力的水平分量與外部牽重力平衡,豎直分量與運動員的體重平衡(忽略滑板的重力和浮力)。該作用力還可以表示為
\mathbf{F}_\mathrm{s} = \rho w h v^2 \sqrt{(\cos 2\theta -1)^2 + \sin^2 2\theta}\cdot\hat{\mathbf{n}} = 2 \rho w h v^2 \sin\theta \cdot \hat{\mathbf{n}} \\
其中單位向量 \hat{\mathbf{n}} 表示水對滑板作用力的方向。容易證明該方向垂直於滑板平面向上,感興趣的讀者可以自行證明。
車輪模型
摩托車的車輪與水的作用要比滑板復雜得多。由於摩托車後輪驅動,前後輪與水之間的作用機制並不一樣。為簡化問題,我們考慮一個具有水平平動速度為 v ,但不旋轉的摩托車車輪(圖 4)。
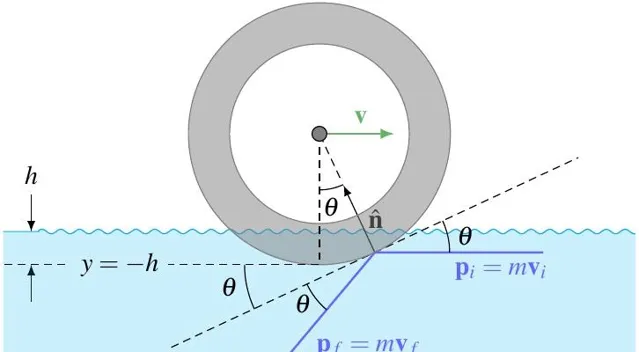
車輪與滑板不同的是,它不再是平面,而是曲面。這表明水在車輪的不同位置施加的力是不同的[4]。考慮角度 \theta 處的一個微元 \mathrm{d}\theta ,由滑板模型可知,在 \theta 處車輪受到水的作用力 \mathrm{d} \mathbf{F} 的方向為
\hat{\mathbf{n}} = \cos\theta\cdot \hat{\mathbf{y}} - \sin\theta\cdot \hat{\mathbf{x}} \\
微元 \mathrm{d}\theta 對應的 y 方向上的長度為
\mathrm{d} y = R\sin\theta \,\mathrm{d}\theta \\
由滑板模型可知,水作用在微元 \mathrm{d}\theta 上的作用力為
\begin{aligned} \mathrm{d} \mathbf{F} &=2\rho w \left( R\sin\theta \,\mathrm{d}\theta \right) v^2 \sin\theta \left(\cos\theta\cdot \hat{\mathbf{y}} - \sin\theta\cdot \hat{\mathbf{x}}\right)\\ &= 2\rho w R v^2 \sin^2\theta \left(\cos\theta\cdot \hat{\mathbf{y}} - \sin\theta\cdot \hat{\mathbf{x}}\right) \,\mathrm{d}\theta \end{aligned} \\
對上式中的 \theta 從 0 到 \theta_{\max} = \arccos(1-h/R) (車輪與水面相交點的角度)積分,可得車輪上受到水的作用力
\begin{aligned} \mathbf{F} &= \int_0^{\theta_{\max}} 2\rho w R v^2 \sin^2\theta \left(\cos\theta\cdot \hat{\mathbf{y}} - \sin\theta\cdot \hat{\mathbf{x}}\right) \,\mathrm{d}\theta\\ &= \frac{2\rho w}{3 R^2} v^2\left[ \left(2hR-h^2\right)^{3/2}\cdot \hat{\mathbf{y}} -h^2 (3R-h)\cdot \hat{\mathbf{x}} \right] \end{aligned} \\
運動方程式
在車輪模型中,我們最終得到了水對車輪的作用力。水對車輪作用力的水平分量與車輪的水平速度方向相反,水會阻礙車輪的運動,使其運動速度減小。水對車輪作用力的豎直分量為摩托車提供了一個向上的托舉力。如果速度足夠大,該托舉力是有可能超過摩托車及人受到的重力的,使車輪在水面上發生彈跳。忽略空氣阻力的影響,車輪發生彈跳並脫離水面時只受重力。由於我們重點關註的是車輪完全或大部份在水面以上時的運動,因此忽略浮力的影響。同時車輪在豎直方向的速度相比於水平方向很小,我們忽略由於豎直方向上的運動導致的水對車輪的作用力。因此,車輪在水平方向的運動方程式為
F_x = m \frac{\mathrm{d}^2 x}{\mathrm{d} t^2} = \begin{cases} \display style - \frac{2\rho w}{3 R^2} \left(\frac{\mathrm{d} x}{\mathrm{d} t}\right)^2 y^2 (3R+y), & y<0\\ &\\ 0, & y\geq 0 \end{cases} \\
車輪在豎直方向的運動方程式為
F_y = m \frac{\mathrm{d}^2 y}{\mathrm{d} t^2} = \begin{cases} \display style \frac{2\rho w}{3 R^2} \left(\frac{\mathrm{d} x}{\mathrm{d} t}\right)^2 \left(-2Ry-y^2\right)^{3/2} - mg, & y<0\\ &\\ - mg, & y\geq 0 \end{cases} \\
需要註意的是,以上兩式已經將 h 替換成為 -y 。由以上兩式構成的微分方程式組即可確定任一時刻車輪的運動狀態。
行駛距離
在車輪模型中,水會阻礙車輪的運動,使其水平運動速度越來越小,最終沒入水中。本節將利用因次分析[5]嘗試尋找車輪沒入水中前在水面行駛的最大距離對各參數的依賴關系。我們將車輪沒入水中一個半徑的深度前所行駛的距離定義為最大行駛距離。最大行駛距離 X 應是水平初速度 v_0 、車輪品質 m 、半徑 R 、寬度 w 、重力加速度 g 、流體(水)密度 \rho 的函式:
X = f\left(v_0,\,m,\,R,\,w,\,\rho,\,g\right) \\
上式中各物理量的因次分別是為:[X] = [R] = [w] = L ,[v_0] = LT^{-1} ,[m] = M ,[\rho] = ML^{-3} ,[g] = LT^{-2} 。取 g 、m 和 R 為基本量,於是有以下無因次關系:
\frac{X}{R} = f\left(\frac{v_0}{\sqrt{gR}},\,\frac{w}{R},\,\frac{\rho R^3}{m}\right) \\
無因次最大行駛距離 X/R 很可能是上式最右端三個無因次數的冪函式之積。由於運動方程式中 \rho 和 w 總是以乘積的形式出現,因此 \rho 和 w 應具有相同的冪次。據此,最大行駛距離對其它參數的依賴關系可能為
\frac{X}{R}= C\cdot \left(\frac{v_0}{\sqrt{gR}}\right)^\alpha\cdot \left(\frac{w\rho R^2}{m}\right)^\beta \\
其中 C 、\alpha 和 \beta 為待定參數。上式表明,\ln(X/R) 與 \ln(v_0/\sqrt{gR}) 可能存線上性關系,稍後我們用運動微分方程式的數值解來驗證這一關系。
結果
雖然由模型確定的微分方程式組沒有解析解,但可以借助電腦求解數值解。假設人車品質 m
= 200 kg,車輪半徑 R
= 0.5 m,車輪寬 w
= 0.1 m,水的密度 \rho
= 1000 kg/m\mathrm{^3}
,重力加速度 g
= 9.8 m/s\mathrm{^2}
。車輪豎直方向初始速度 v_y=0
m/s,水平方向初始速度 v_0
= 20, 30 或 40 m/s。車輪的初始位置為 x_0
= y_0
= 0 m。套用 MATLAB 中的函式
ode45
對車輪運動方程式進行求解,得到的結果如圖 5 所示。
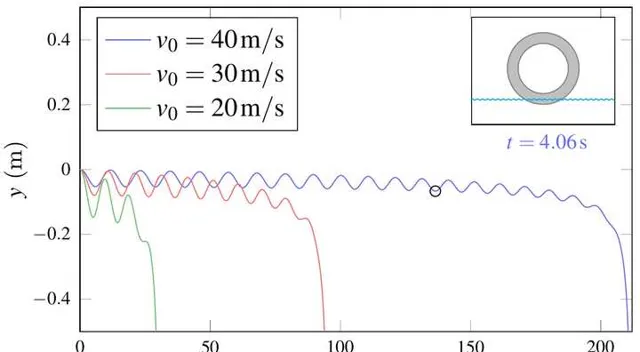
結果表明,摩托車初始水平速度越大,在水面行駛的距離就越遠。水平初始速度為 40 m/s 時,摩托車在水面行駛的距離超過 220 米。由於水的作用,車輪在行駛的過程中會一直在水面彈跳,但隨著速度的下降,彈跳的振幅越來越小,最終沈入水中。水平初速度越小,車輪在水面完成的彈跳次數也越小。當水平初速度小於 10 m/s 左右(臨界速度)時,車輪在水面無法完成一次彈跳。並且車輪的整運動過程中,水對車輪的豎直作用力都小於人和摩托車的重力。因此,要想摩托車能夠在水面行駛,水平初速度必須大於某個臨界速度(水面行駛所需的最小初速度),稍後我們討論臨界速度的具體大小。
初始高度
如果車輪離水面的初始高度 y_0 > 0,是否會更有利於摩托車在水面行駛出更大的距離呢?透過調整車輪距離水面的初始高度 y_0 ,我們發現當 y_0 降低為 0 時,在各個初始水平速度下,車輪在水面行駛的距離都是最大。圖 6 顯示的是初速度為 v_0 = 40 m/s 的情況。因此,摩托車在陸地上的跑道終點應該盡可能與水面相平,這樣才能使摩托車在水面行駛更大的距離。
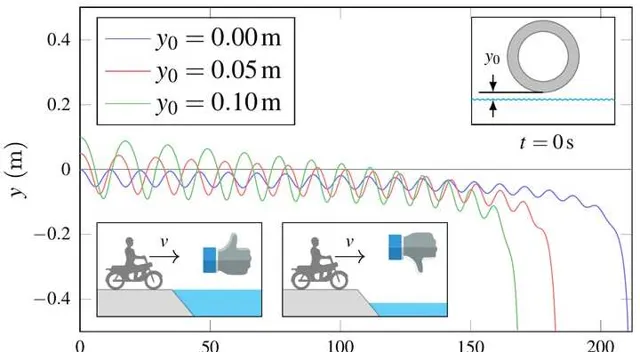
行駛距離
接下來本文研究一下人車品質、車輪半徑和寬度對水面行駛距離的影響。透過在圖 5 模擬的基礎上,對人車品質 m 、車輪半徑 R 和寬度 w 分別增加或降低 50%,計算得到各速度下的水面行駛距離如圖 7 所示。結果表明:人車品質 m 越小,車輪半徑 R 和寬度 w 越大,越有利於摩托車在水面上行駛出更大的距離。
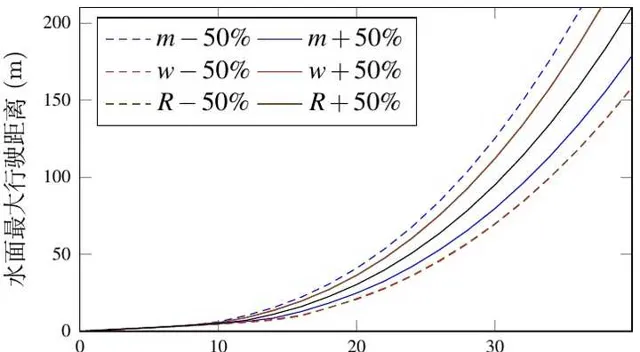
在關於行駛距離的模型中,本文透過因次分析得出 \ln(X/R) 與 \ln(v_0/\sqrt{gR}) 可能存線上性關系。為驗證因次分析得到的結論,對圖 7 中的速度和行駛距離無因次後取對數得到 \ln(X/R) 與 \ln(v_0/\sqrt{gR}) 的關系( 圖 8)。結果顯示:不同參數取值情況下,\ln(X/R) 與 \ln(v_0/\sqrt{gR}) 都存在兩段線性關系。
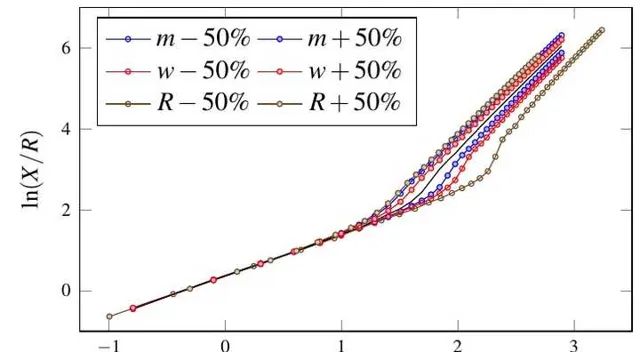
第一段線性關系:車輪水平初速度小於臨界值,水對車輪的作用力不足以抵抗摩托車的重力,摩托車無法在水面行駛。從圖 8 可以看出,第一段線性關系的斜率和截距與 m 、w 和 R 無關。因此,在第一段線性關系 \beta_1 = 0,即:
\ln\left(\frac{X}{R}\right) = \alpha_1 \ln \left(\frac{v_0}{\sqrt{gR}}\right) + \ln C_1 \\
其中 \alpha_1 和 C_1 的下標「1」是用來區別於第二段線性關系。透過擬合可得 \alpha_1 = 1 和 C_1 = 1.4687。
第二段線性關系:車輪水平初速度大於臨界值,水對車輪的作用力可以支持摩托車在水面行駛一段距離。我們發現在這種情況(初速度大於臨界值)下,改變 w 和改變 R 對 X 的影響幾乎完全相同(圖 7)。對 X 而言,R 和 w 應有相同冪次,即 2\beta - \alpha_2 /2 - 1 = \beta 。因此,第二段線性關系的形式為:
\ln\left(\frac{X}{R}\right) = \alpha_2 \ln \left(\frac{v_0}{\sqrt{gR}}\right) + \left(\frac{\alpha_2}{2} - 1\right) \ln\left(\frac{w\rho R^2}{m}\right)+ \ln C_2 \\
圖 8 中各線的第二段斜率幾乎相同,該斜率即為 \alpha_2 ,透過擬合可得 \alpha_2 = 2.9365 和 C_2 = 0.2344。上式表明,各參數下 \ln(X/R) 和 \alpha_2 \ln (v_0/\sqrt{gR}) + (\alpha_2 /2-1) \ln(w\rho R^2/m) 存在統一的斜率為 1 的線性關系(圖 9)。
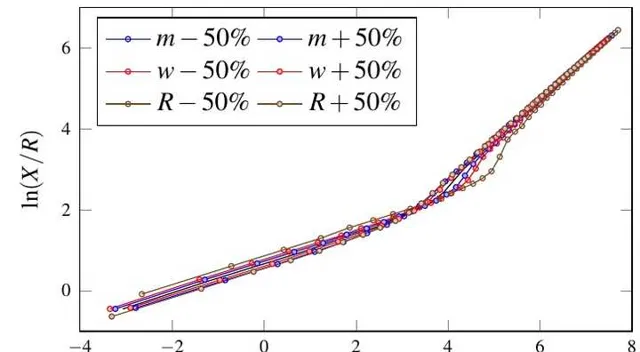
第一段線性關系的直線方程式與第二段線性關系的直線方程式的交點即為臨界速度。據此可求得臨界速度的運算式:
v_{\min} = \left(\frac{C_1}{C_2}\right)^{\frac{1}{\alpha_2-\alpha_1}} \cdot \left( \frac{m}{w\rho R^2} \right)^{\frac{\alpha_2/2-1}{\alpha_2-\alpha_1}}\cdot \sqrt{gR} \\
套用上述無因次分析結果,我們對人車品質 m = 200 kg,車輪半徑 R = 0.5 m 和寬度 w = 0.1 m 的情況進行預測(圖 10)。
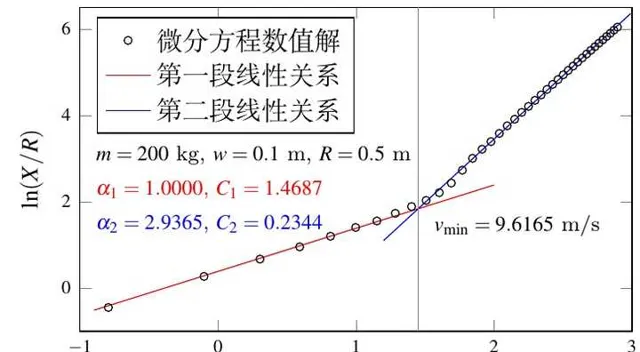
圖 10 顯示,預測結果(兩段線性關系和臨界速度)與微分方程式數值解結果都吻合得很好。
結論
本文針對摩托車為什麽能在水面上行駛這個問題進行了建模分析。透過參考滑板滑水原理,建立了車輪的運動方程式。車輪運動方程式的數值解表明:摩托車想要能夠在水面行駛,水平初速度必須大於臨界速度。水平初速度越大,人車品質越小,車輪半徑和寬度越大,越有利於車輪在水面上行駛出更大的距離。特別的,對於人車品質 m = 200 kg,車輪半徑 R = 0.5 m,車輪寬 w = 0.1 m 的情況,其臨界速度約為 10 m/s。在水平初速度 v_0 = 40 m/s 時,摩托車在水面行駛的最大距離可達 220 米。
此外,本文還嘗試利用因次分析嘗試尋找水面最大行駛距離對各參數的依賴關系,並透過運動方程式的數值解得到了驗證。
參考資料
[1] Mythbusters. Motorcycle water ski, 2017: https://www. youtube.com/watch? v=27BBPlnuAaA
[2] Sarah Winkler. How waterskiing works, 2009: https:// adventure.howstuffworks.com /outdoor-activities/water-sports/wakeboarding.htm
[3] WAKEBOARDING. The physics of wakeboarding and water skiing, 2021: https://www. surfertoday.com/wakeboa rding/the-physics-of-wakeboarding-and-water-skiing
[4] David Zaslavsky. Riding on water, 2013: https://www. ellipsix.net/blog/2013/ 06/riding-on-water.html
[5] Tan QM. Dimensional analysis: with case studies in mechanics. 2011.










