先寫結論: 九進制對文明來說其實是非常不錯的進制,雖然可能不如八進制、十六進制、十二進制,但和十進制可能半斤八兩,如果按照九進制生活,文明的數學發展水平發展速度並不會和十進制有太大的差異,至於奇數和偶數的概念,更是很早能被發現的,不值一提。
不妨我們 身臨其境 一下,以下內容均為 九進制文明視角 。
為了描述方便,在這個視角下,不存在「九/9」這個稱謂,所有「九」的稱謂都被讀作「十」,所以這個文明也自稱使用「十進制」。而這個世界中的「百」、「千」、「萬」即代表了人類十進制下的 81、729、6561……
【再次提示】:請務必忘記人類使用的十進制!
1)算數
1a)乘法口訣
首先是這個文明中裏耳熟能詳的 「八八乘法口訣表」:
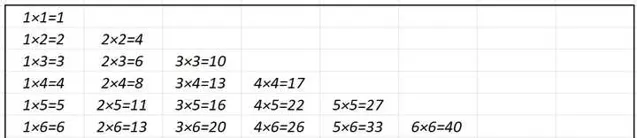
據說小孩子們最喜歡的口訣是「六六四十」,聽起來就很順。
為了提升孩子們的算術水平,學校組織學生們去參加了「四張撲克牌算 26 點」的活動,當然,算多少點還是有點爭議,畢竟大家太熟悉 3 的倍數了,有老師建議「算 22 點」是更合適的,這能鍛煉孩子們對 2 、5 的倍數的理解。
這個文明有一個著名的小說叫「東遊記」,棠僧經歷了八八七十一難才取到真經。
1b)數的整除
對於這個文明,3 和 6 是這個世界最耳熟能詳的數位,畢竟這些數的倍數末尾都是 3、6、0。
另外比較有名的說法是「卅數」「丗數」「川數」,這個說法比「奇數」、「偶數」更出名。
「卅數」是指除以 3 余數為 1 的數,也即末尾為 1、4、7 的數;「丗數」是指除以 3 余數為 2 的數,也即末尾為 2、5、8 的數;
「川數」是指能被 3 整除 的數,也即末尾為 3、6、0 的數;
早年的數學研究很多就是圍繞著「卅數」和「丗數」展開的。
當然,由於這個國家的性別依舊是 2 個,很快也誕生了「奇數」和「偶數」的概念:偶數是 2 的倍數,奇數不是 2 的倍數。
怎麽看一個數是奇數還是偶數呢?
先說一個概念叫「奇數因子」:1、3、5、7。
然後對於不小於兩位的數,我們就看「奇數因子」有幾個,如果有奇數個,那這個數就是奇數,比如 1 2、4 7 、 333 、6 5 6……反之就是偶數,比如 35 、40、 57 6、 7 28 1 ……
小學數學老師會告訴你,有一個巧妙的方法,可以迅速判定一個數是否為 2、4、8 的倍數: 看它們的數位和是否為 2、4、8 的倍數 。在數學比較好的國度中,8 的倍數們:8、17、26、35、44、53、62、71 都是耳熟能詳的。
3 的倍數就不講了。判斷一個數是否是 6 的倍數的方法,就是先看末尾是不是 0/3/6,再看看是不是 2 的倍數。
至於一個數是否為 5、11 的倍數,小學奧賽老師會告訴你:看這個數奇數位的和與偶數位的和之差是否為 5、11 的倍數。比如 5478,個位和百位的和 4+8=13;十位和千位的和 5+7=13,所以這個數是 5、11 的倍數。再比如 35634,奇數位之和 3+6+4 =14;偶數位之和 5+3=8,而 14-8=5,因此 35634 是 5 的倍數,但不是 11 的倍數。
至於一個數是否為 7,14,15 的倍數,一般是超綱內容。超微資深一些的老師會告訴你,有一個簡便一些的判別方法,註意到 888 是 7,14,15 的倍數(888=8×7×14=4×14×15),可以將一個大數每 3 位一分割,然後求和,如果這個是 7,14 的倍數,原數也是 7,14 的倍數。
舉個例子:23456122,我們先算出:23+456+122= 612,612/7=78 是 7 的倍數,因此 23456122 是 7 的倍數。1c)電腦數學
後來誕生了電腦。這個文明對 3 更熟悉,因此一開始電腦是 3 進制的,畢竟 3 進制表示數據是非常高效的。但後來發現,3 狀態的元器件造價太貴,2 狀態的元器件要便宜得多,掙紮了十幾年後,終於還是把電腦換成了二進制的。
程式設計師們對 2 的冪次非常熟悉:2,4,8,17,35,71,152,314,628,1357……
考慮到 2 的 10 次方是 628,所以每年的 6 月 28 日被認為是「程式設計師節」。
人們發現 2 的 11 次方是 1357,一個這麽偶數的數,居然每一位都是奇數,還是等差數列,太神奇了!
人們還發現 2 的 21 次方為 878162,這個數和 1000000 僅僅差了 1.07%,非常接近。
於是 1MB = 2^21 B = 878162 B
2)數論
2a)質數
這個國家同樣對數論感興趣,他們比較熟悉 100 以下的 24 個質數:
2、3、5、7、12、14、18、21、25;32、34、41、45、47、52、58、65、67;
74、78、81、87。
100 以內最大的質數是 87。
有意思的是:對於大於 3 的質數,卅數和丗數各有 11 個,很均衡。
業余數學家費牛發現:
都是質數。於是他猜想,2^2^n + 1 都是質數。
但後來人們發現,2^2^5 + 1 = 12068657455 = 782 × 13542217,這個數不是質數!
這個世界裏還有一個很著名的數論入門題,它常常用來辨識一個人有沒有數論天賦:
111111……(n個1) 是不是質數?沒有數論天賦的人,可能絞勁腦汁很久都想不出來。但是著名天才數學家低斯,10 歲的時候就用巧妙的方法解決了。
要不你也來試試?
提示:分奇數和偶數討論,在這個世界裏 10=3×3。2b)走馬燈數
在這個文明裏,人們也會研究其他進制,發現在其他進制中,普遍存在「走馬燈數」,也就是說,這個數的倍數會是這個數所有數位的重新組合,而且順序也不變,只是起點和終點變了。
比如:
但唯獨 10 進制,似乎沒有這樣的「走馬燈數」。
後來數學家們發現,因為 10=3×3 是平方數,透過原根的相關知識我們可以證明,在平方數進制下,是不存在走馬燈數的,真可惜!
2c)黑洞數
在這個文明裏,雖然沒有人們耳熟能詳的「走馬燈數」,卻有另一個耳熟能詳的數,它是 62853。這個數被成為「黑洞數」。
黑洞數又稱陷阱數,是類具有奇特轉換特性的整數。任何一個數位不全相同整數,經有限「重排求差」操作,總會得某一個或一些數,這些數即為黑洞數。
比如 31467,將其重新排序後最大的數是 76431 ,最小的數是 13467 ,相減以後得到 62853;
然後繼續以上操作:86532 - 23568 = 62853
咦,居然沒有發生變化?
這就是黑洞數。
事實上,已經證明,1~4 位數都不存在「黑洞數」,只能跌入迴圈,於是 62853 是最小的黑洞數。而且,並不是所有的 5 位數都能跌入「黑洞數」的(只有 5210 種初始值可能會跌入這個迴圈,占 5.8%),更大的可能是,跌入一個「大迴圈」(除了 11111 的倍數外,其余情況均是如此):
74832 -> 63843 -> 52854 -> 60873 -> 83841 -> 74832:因此「黑洞數」 62853 顯得彌足珍貴,很多人都把它設定成密碼。
( 程式碼參見附錄 )
3)小數
3a)小數的性質
在該文明的「知也」上,數學區會有一個月經問題:0.8888888…… 是否等於 1 ?
有一個高贊回答是:註意到 1/2 = 0.4444444……,因此 1/2 × 2 = 0.888888…… 所以 0.888888…… 等於 1 。
也對,這個文明的小數發展的更早,畢竟 1/2 = 0.444444……,所以人們很早就發現了「迴圈小數」。
在進行 10 以下的等分時,迴圈節最多 3 位,也比較容易記憶,數學老師會要求背誦下來。
3b)圓周率
關於「圓周率」,一開始,人們認為圓周率大概比 3.12 稍微大一點。
巍國數學家劉輝在自己的【八章算數】裏仔細研究了下,認為圓周率等於 3.1242,這個數大概是能被整除的。
後來錦國的科學家孫退乎利用「割圓術」,發現劉輝的結果不太精確。他算出圓周率在 3.1241881~3.1241882 之間。
並且給出了兩個近似值:
人們發現,圓周率小數點後前 7 位的每一位都是 2 的冪次,人們認為這應該不是巧合。因此認為圓周率後的每一位可能都是 2 的冪次。
直到一千年後,數學大發展,計算圓周率的方式也被進一步最佳化了,人們發現圓周率後第 12 位是 7,推翻了這一猜想。
現在人們知道,圓周率大約是 3.124188124074427883……
3c)其他常數
後來,科學家發明了對數。定義如果以 10 為底的對數為 lg
於是 lg2≈0.275, lg3=1/2≈0.444,lg5≈0.653
後來馬頓發明了微積分,但與此同時祛拳尼茲也獨立發現了微積分,兩個人大吵一架,不歡而散。
不過這不重要,重要的是,大家發現 e ≈ 2.641557364 這個數似乎也是一個超越數。
註:以上只是該文明的內容提綱,後續內容可以參見專欄系列文章:
附錄:「黑洞數」計算程式碼(好久沒用 python,復習一下):
# Calulate the Blackhole Number in Base n
# Author: PlusZeng
# Date: created: 2022/12/4, modified: 2022/12/19
import
math
def
list2chr
(
a
,
n
):
tmp
=
''
if
n
<=
10
:
for
i
in
a
:
tmp
+=
str
(
i
)
if
n
>
10
:
for
i
in
a
:
if
i
<
10
:
tmp
+=
str
(
i
)
elif
i
<
36
:
tmp
+=
chr
(
i
+
55
)
elif
i
<
62
:
tmp
+=
chr
(
i
+
61
)
else
:
tmp
+=
'('
+
str
(
i
)
+
')'
return
tmp
def
root_10_to_n
(
x
,
n
,
x_digit
):
result
=
[];
p
=
n
**
(
x_digit
-
1
);
while
(
p
>=
1
):
result
.
append
(
math
.
floor
(
x
/
p
))
x
%=
p
;
p
/=
n
;
return
result
def
minus_hole
(
x
,
root_n
,
x_digit
):
y_min
=
sorted
(
x
);
a_max
=
0
;
a_min
=
0
;
for
i
in
range
(
0
,
x_digit
):
a_min
+=
int
(
y_min
[
i
])
*
root_n
**
(
x_digit
-
i
-
1
)
a_max
+=
int
(
y_min
[
i
])
*
root_n
**
i
return
root_10_to_n
(
a_max
-
a_min
,
root_n
,
x_digit
)
def
cal_hole_in_base_n
(
x_digit
,
n
):
cirDict
=
{};
for
i
in
range
(
n
**
(
x_digit
-
1
),
n
**
x_digit
):
numList
=
[];
numList
.
append
(
root_10_to_n
(
i
,
n
,
x_digit
));
tmp
=
0
;
is_circle
=
0
;
while
(
is_circle
==
0
):
numList
.
append
(
minus_hole
(
numList
[
tmp
],
n
,
x_digit
))
tmp
+=
1
for
j
in
range
(
tmp
-
1
,
-
1
,
-
1
):
if
numList
[
tmp
]
==
numList
[
j
]:
is_circle
=
1
break
cirList
=
list2chr
(
numList
[
j
],
n
)
for
k
in
range
(
j
+
1
,
tmp
):
cirList
+=
'->'
+
list2chr
(
numList
[
k
],
n
)
if
cirDict
.
get
(
cirList
)
is
None
:
cirDict
[
cirList
]
=
[
list2chr
(
numList
[
0
],
n
)]
else
:
cirDict
[
cirList
]
.
append
(
list2chr
(
numList
[
0
],
n
))
for
i
in
cirDict
.
keys
():
print
(
i
+
' : '
+
str
(
len
(
cirDict
[
i
]))
+
';'
)
if
__name__
==
'__main__'
:
print
(
'Input the base: '
)
n
=
int
(
input
())
print
(
'Input the max digits: '
)
x_digit
=
int
(
input
())
for
i
in
range
(
1
,
x_digit
+
1
):
print
(
'
\n
'
+
str
(
i
)
+
' digits'
)
cal_hole_in_base_n
(
i
,
n
)
print
(
'Done!'
)










