數學界有哪些通俗易懂的 open problem？

1.\[\prod\limits_{k = 1}^\infty {{{\left( {1 - {x^k}} \right)}^{24}}} \] 冪級數展開的系數中是否有0？

即證明或推翻: \[\prod\limits_{k = 1}^\infty {{{\left( {1 - {x^k}} \right)}^{24}}} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + ...\] 中 \[{x^n}\] 的系數 \[{a_n} \ne 0\] 恒成立，目前電腦已經驗證了所有 \[n < 816212624008487344127999\] ，沒有發現反例，也沒有證明。

前幾項如下：

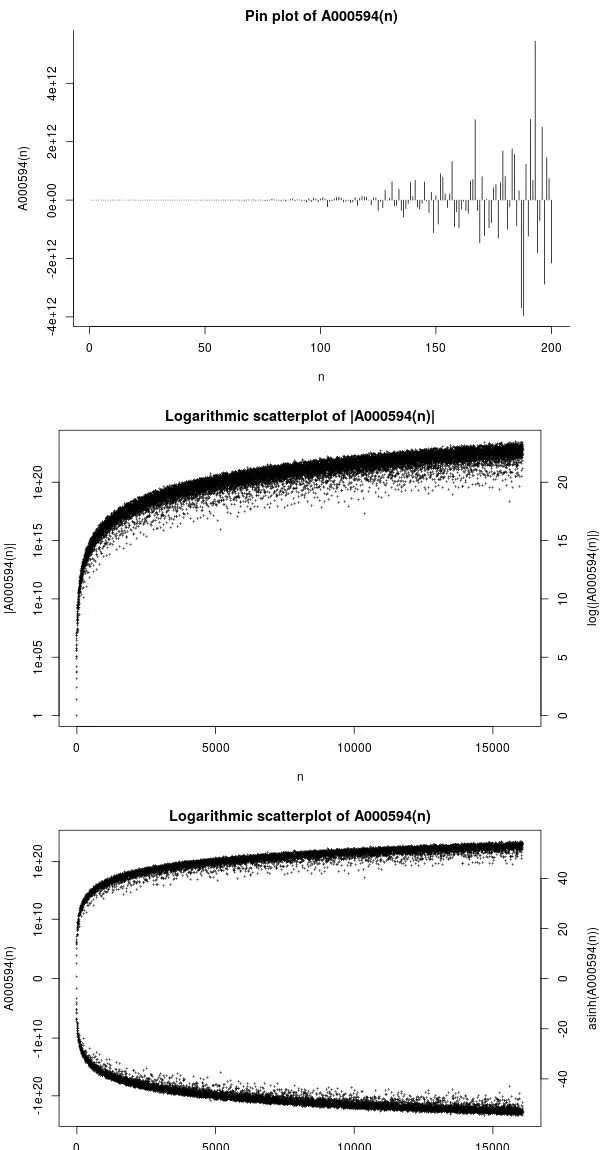
2.數列 \[{a_1} = {a_2} = 1,{a_n} = {a_{n - {a_{n - 1}}}} + {a_{n - {a_{n - 2}}}}\left( {n \ge 3} \right)\] 是否是有限數列？

若存在某個 \[n \ge 3\] 使得 \[{a_{n - 1}} \ge n\] ，則下標 \[n - {a_{n - 1}} < 1\] ，遞推無法進行，數列到此為止，便為有限數列，但目前沒人能證明這一點。

前幾項如下：

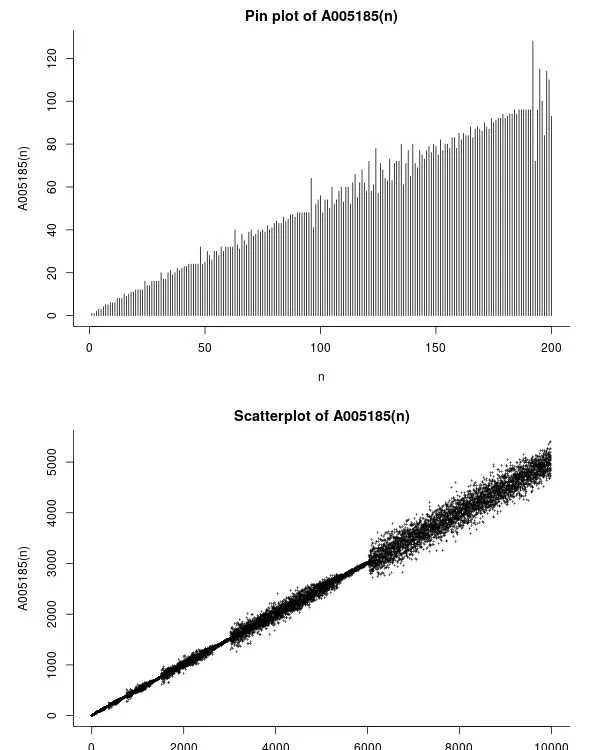
3.Flint Hills Series是否收斂？

即求和 \[\sum\limits_{n = 1}^\infty {\frac{{{{\csc }^2}n}}{{{n^3}}}} \] 是否收斂？此問題與 \[\pi \] 的無理測度有關，目前還沒被證明。

4. 對於大於等於2的正整數，是否總有 \[\left\lfloor {\frac{{{3^n}}}{{{2^n}}}} \right\rfloor = \left\lfloor {\frac{{{3^n} - 1}}{{{2^n} - 1}}} \right\rfloor \] ？

其中 \[\left\lfloor x \right\rfloor \] 表示向下取整，如 \[\left\lfloor \pi \right\rfloor = 3,\left\lfloor {4.7} \right\rfloor = 4\]

看著很簡單，實際上難度很高

5.平面上n條兩兩相交的線最多能交出多少個不重疊的三角形？

又稱Kobon三角形問題，交法具體見下圖：

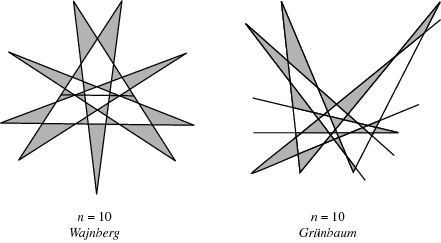
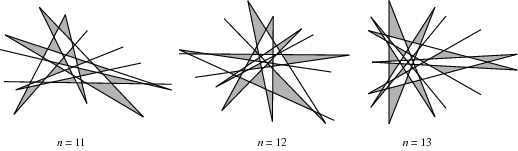
目前已經證明上界是 \[\left\lfloor {\frac{{n\left( {n - 2} \right)}}{3}} \right\rfloor \] ，前幾項是 0, 0, 1, 2, 5, 7, 11, 15, 21...

6.三維空間中至多有幾條異面直線兩兩距離相等？

又稱Touching Cylinders Puzzle，目前最好的答案是七，不知道有沒有更大的。

具體可以見：

7.平面內能覆蓋住所有長度為1的曲線的最小圖形面積是多少？

此問題又稱The Worm Problem，即要求在平面上尋找一個面積最小的(凸)區域,使得任何一條長為1的平面曲線都能夠透過旋轉和平移完全放入該(凸)區域之中。目前最優解如下：

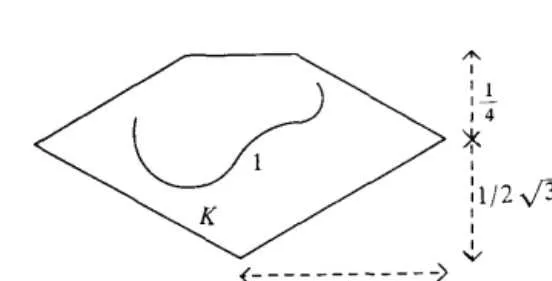
8.哪些正整數不能被表示為 \[xy + yz + zx,1 \le x \le y \le z\] 且 \[x,y,z \in {N^ + }\] 的形式？

已經證明 1, 2, 4, 6, 10, 18, 22, 30, 42, 58, 70, 78, 102, 130, 190, 210, 330, 462 這些數無法表示，且至多還存在一個 \[ \ge {10^{10}}\] 的數滿足，但目前無人能證明或推翻其存在性。

先寫這些，日後慢慢補充。。。