背景介紹:
一般而言,如果在空曠環境下,GNSS的定位精度已經很高,也就沒有很高的必要性考慮利用5G訊號進行定位。
相對而言,就亟需在城市化的環境下,比較GNSS和5G的定位效能。在這種場景下,對GNSS/5G定位造成主要影響的就是多路徑幹擾——眾所周知,GNSS多路徑誤差一般幾米~幾百米不等。接收機利用一些傳統的抗多徑幹擾演算法,可以很容易地抑制大於約20公尺以上多徑誤差。根據一些最新的研究成果顯示,5G訊號的多徑誤差,在仿真條件下,至少也在米級範圍 [1] ,與GNSS的誤差範圍相近。
通常情況下,使用者相對於5G基站/GNSS衛星的仰角越低,觀測量中存在多徑誤差的機率越大,具體的發生過程,可以參考下面兩幅示意圖:
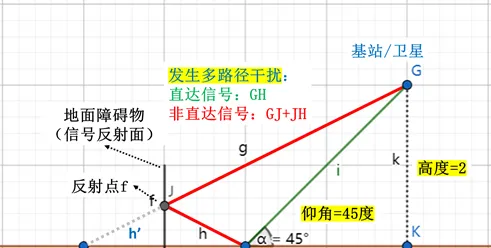
當基站/衛星與使用者映像點的連線穿過地面障礙物的橫截面,此時就會在使用者端發生多徑幹擾。
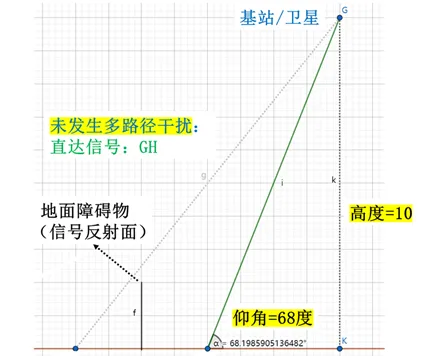
當基站/衛星的高度增加,此時它們相對於使用者的仰角也變大。觀察示意圖發現,仰角越大,多路徑幹擾發生的機率越小(因為基站/衛星與使用者映像點的連線穿過地面障礙物橫截面的機率變小了)。
5G訊號的基站高度一般為幾十米,這就導致使用者相對其仰角一般比較低。從全球範圍來看,GNSS衛星可以覆蓋使用者0~90度的仰角範圍,因此,GNSS訊號相對於5G訊號在城市環境下,理論上,發生多徑幹擾的機率更小。
一些假設
根據以上分析,我們可以在給出以下假設的前提下,定量地比較GNSS/5G的定位精度:
假設一:
為了簡化分析,忽略高程位置,只考慮使用者水平面內的二維位置座標;
假設二:
5G基站和GNSS衛星幾何構型一致,如下圖所示:

假設三:
GNSS和5G訊號的多徑誤差在0~20m的範圍內;
假設四:
當5G基站/GNSS衛星的仰角不大於20度時,一定發生多路徑幹擾;當仰角大於20度時,則不會發生多徑幹擾;
假設五:
不考慮時鐘及其他隨機雜訊對定位精度的影響。
利用最小平方計算使用者位置
{\mathbf{x}} = {\left[ {{x_r},{y_r}} \right]^T}
使用者到衛星A的距離函式為
l_r^{\left( A \right)} = \sqrt {{{\left( {{x^{\left( A \right)}} - {x_r}} \right)}^2} + {{\left( {{y^{\left( A \right)}} - {y_r}} \right)}^2}}
其中, \left( {{x^{\left( A \right)}},{y^{\left( A \right)}}} \right) 表示衛星A的位置座標。
為了利用最小平方求解使用者位置,必須要將上面的模型進行線性化(利用泰勒展開),得到:
l_r^{\left( A \right)} \approx {r^{\left( A \right)}} + {\left. {\frac{{\partial l_r^{\left( A \right)}}}{{\partial {x_r}}}} \right|_{{x_r} = {x_0}}}\left( {{x_r} - {x_0}} \right) + {\left. {\frac{{\partial l_r^{\left( A \right)}}}{{\partial {y_r}}}} \right|_{{y_r} = {x_0}}}\left( {{y_r} - {y_0}} \right)
其中,
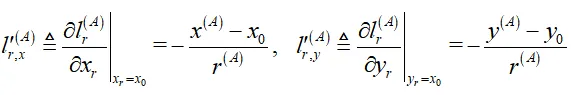
並且 {r^{\left( A \right)}} 表示使用者到衛星A的幾何距離; {\mathbf{x}} = \left[ {{x_0},{y_0}} \right]^T 表示使用者位置初始值。
綜上,觀測矩陣和觀測量向量分別為
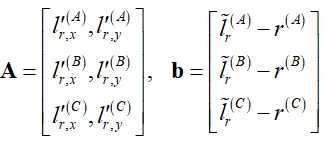
\delta {\mathbf{x}} = {\left( {{{\mathbf{A}}^T}{\mathbf{A}}} \right)^{ - 1}}{{\mathbf{A}}^T}{\mathbf{b}}
{\mathbf{x}} = {{\mathbf{x}}_0} + \delta {\mathbf{x}}
構造存在多徑誤差的觀測量
\tilde l_r^{\left( A \right)}{\text{ = }}\sqrt {{{\left( {{x^{\left( A \right)}} - {x_r}} \right)}^2} + {{\left( {{y^{\left( A \right)}} - {y_r}} \right)}^2}} + {B_{mul}}
其中, \left[ {{x^{\left( A \right)}},{y^{\left( A \right)}}} \right] 和 \left[ {{x_r},{y_r}} \right] 在這裏都表示真實的衛星位置和使用者位置座標;
{B_{mul}} 表示多徑誤差(這裏考慮0~20m範圍內的隨機值)。
仿真實驗及結果
根據「一些假設」一節中的討論,利用簡單的仿真實驗來比較GNSS訊號和5G訊號在城市環境下的定位精度。
| 仿真參數 | 設定值 |
| 產生多徑仰角範圍 | 0~20度 (超過20度則無多徑發生) |
| 5G基站的最大仰角 | 30, 40, 50, 60, 70, 80度 |
| GNSS衛星的最大仰角 | 90度 |
| 多徑誤差的範圍 | 0~20公尺 |
| 蒙特卡羅實驗次數 | 10000次 |
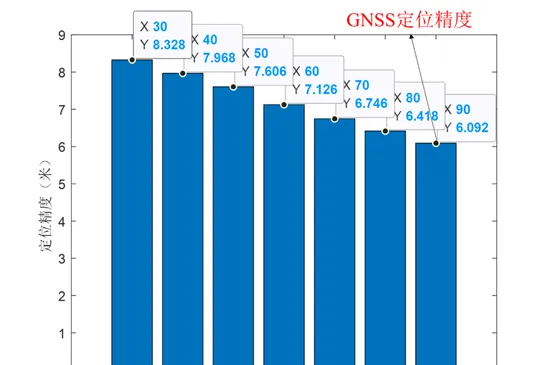
下面兩圖展示了最終的仿真結果。根據仿真結果判斷,5G基站的最大仰角(或基站高度)越高,定位精度越高。GNSS在仿真中的定位精度最高,約6公尺;隨著5G基站最高仰角的增加,其定位精度也逐漸提高;當基站的最高仰角為30度時,GNSS相對於5G定位精度有26.86%的提升,當仰角增大到80度時,提升程度變小,僅為5%左右。

結論
這個回答,定量分析了城市環境下,多路徑對GNSS訊號和5G訊號定位精度的影響。使用者相對於GNSS衛星或5G基站的仰角,影響著兩種無線訊號發生多路徑幹擾的機率。為了能具體分析定位精度,回答中,對仿真實驗進行了大量簡化,設定了很多假設,實驗參數設定了很多限制條件,可能在實際環境下,有些假設並不能嚴格滿足,因此實驗結果僅供參考。但可以確定的是,如果不能很好地解決多路徑對5G訊號定位的影響,在短時間內,其定位精度還是沒有辦法超越GNSS。
參考
- ^ K. Shamaei, 「Exploiting Cellular Signals for Navigation: 4G to 5G,」 University of California, Irvine, Irvine, 2020.
- ^ 謝鋼, GPS原理與接收機設計. 北京: 電子工業出版社, 2009.











