接下来用七种方法证明 \sin'x=\cos x ,当然方法肯定还有很多:
1. 教科书式证法
\begin{align} (\sin x)'& =\lim_{\Delta x \rightarrow 0}{\frac{\sin(x+\Delta x)-\sin x}{\Delta x}} \\ & =\lim_{\Delta x \rightarrow 0}{\frac{\sin x\cos \Delta x+\cos x\sin \Delta x-\sin x}{\Delta x}} \\ & =\cos x\lim_{\Delta x \rightarrow 0}{\frac{\sin \Delta x}{\Delta x}} +\sin x\lim_{\Delta x \rightarrow 0}{\frac{\cos \Delta x-1}{\Delta x}} \\ & = \cos x \end{align}
过程中用到了如下两个极限:
\lim_{x \rightarrow 0}{\frac{\sin x}{x}}=1
\lim_{x \rightarrow 0}{\frac{\cos x-1}{x}}=\lim_{x \rightarrow 0}{\frac{1-2\sin^2 \frac{x}{2}-1}{x}} =-\lim_{t \rightarrow 0}{\frac{\sin^2 t}{t}} =-0\cdot1=0
对于第一个极限,用教科书式的面积法证明:
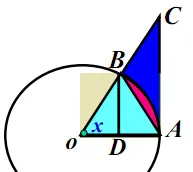
因为x\in(0,\frac{\pi}{2}) 时 , S_{\triangle AOB}<S_{扇形 AOB}<S_{\triangle AOC} ,故 \sin x<x<\tan x ,变换得 \cos x<\frac{\sin x}{x}<1 ,由三角函数的奇偶性知,在 (-\frac{\pi}{2},0)\cup(0,\frac{\pi}{2}) 上述不等式也成立,最后利用夹逼定则得 \lim_{x \rightarrow 0}{\frac{\sin x}{x}}=1 .
2. 教科书式证法之二
\begin{align} (\sin x)'& =\lim_{\Delta x \rightarrow 0}{\frac{\sin(x+\Delta x)-\sin x}{\Delta x}} \\ & =\lim_{\Delta x \rightarrow 0}{\frac{2\cos\frac{2x+\Delta x}{2}\sin\frac{\Delta x}{2}}{\Delta x}} \\ & =\lim_{\Delta x \rightarrow 0}{\frac{2\sin\frac{\Delta x}{2}}{\Delta x}} \lim_{\Delta x \rightarrow 0}{\cos(x+\frac{\Delta x}{2})} \\ & = \cos x \end{align}
过程用到了极限 \lim_{x \rightarrow 0}{\frac{\sin x}{x}}=1 ,和差化积公式
\sin\alpha-\sin\beta=\sin\left(\frac{\alpha+\beta}{2}+\frac{\alpha-\beta}{2}\right)-\sin\left(\frac{\alpha+\beta}{2}-\frac{\alpha-\beta}{2}\right)=2\cos\left(\frac{\alpha+\beta}{2}\right)\sin\left(\frac{\alpha-\beta}{2}\right)
还有 \cos x 的连续性( \lim_{x \rightarrow x_0}{\cos x}=\cos x_0 ).
关于连续性的教科书式证明如下:
|\sin x-\sin x_0|=2\left |\cos\frac{x+x_0}{2}\sin\frac{x-x_0}{2}\right |< |x-x_0|\rightarrow0\\ |\cos x-\cos x_0|=2\left |\sin\frac{x+x_0}{2}\sin\frac{x-x_0}{2}\right |< |x-x_0|\rightarrow0
故 \sin x,\cos x 连续.
此处用到了 \sin x< x\quad(x>0) 以及三角函数的有界性.
3. 匀速圆周运动法
一个做匀速圆周运动的物体:
\bm r=r\cos\omega t\bm i+r\sin\omega t\bm j
\bm v=\frac{\mathrm d \bm r}{\mathrm dt}=\omega r\cos'\omega t\bm i+\omega r\sin'\omega t\bm j
而 \bm r\bot\bm v ,又 v=\omega r ,故
\bm v=\omega r\cos(\omega t+\frac\pi2)\bm i+\omega r\sin(\omega t+\frac\pi2)\bm j=-\omega r\sin\omega t\bm i+\omega r\cos\omega t\bm j
对比得:
\sin'x=\cos x
\cos'x=-\sin x
4. 弧长公式证明法
用参数方程表示的曲线 \begin{cases} x=x(t) \\ y=y(t) \end{cases} 的弧长公式为 L=\int_{t_1}^{t_2}\sqrt{[x'(t)]^2+[y'(t)]^2}\mathrm dt
单位圆的参数方程为 \begin{cases} x=\cos t \\ y=\sin t \end{cases} ,因此角 x 对应的弧长为: x=\int_{0}^{x}\sqrt{(\cos't)^2+(\sin't)^2}\mathrm dt
将两端求导,并加上单位圆方程,得到:
\begin{cases} \sin^2x+\cos^2x=1&(1)\\ (\sin'x)^2+ (\cos'x)^2=1&(2)\end{cases}
对方程(1)两端求导,得到
2\sin x\sin'x+2\cos x\cos'x=0
移项并平方
\sin^2 x(\sin'x)^2=\cos^2 x(\cos'x)^2
用方程(2)干掉 \cos'x
\sin^2 x(\sin'x)^2=\cos^2 x[1-(\sin'x)^2]
整理得
(\sin'x)^2=\cos^2 x
通过几何直观看出二者同号:
\sin'x=\cos x
同理
\cos' x=-\sin x
5. 反函数法
考虑单位圆的右半圆周 x=\sqrt{1-y^2} ,点 (1,0) 与 (x_0,y_0) 之间的弧长为:
s=\int_{0}^{y_0}\sqrt{1+x'^2}\mathrm dy=\int_{0}^{y_0}\frac{1}{\sqrt{1-y^2}}\mathrm dy
在单位圆弧长公式中,右边是一个正弦值的函数,左边的弧长可以看做弧度制下的角度,这正好与反正弦函数的定义相符.
因此我们可以定义弧度制下的反正弦函数:
\arcsin x:=\int_{0}^{x}\frac{1}{\sqrt{1-t^2}}\mathrm dt
易知
(\arcsin x)'=\frac{1}{\sqrt{1-x^2}}
今 y=\sin x 即 \arcsin y =x ,两端求导得
\frac{y'}{\sqrt{1-y^2}}=1
y'=\sqrt{1-y^2}=\sqrt{1-\sin^2x}=\cos x
即
\sin 'x=\cos x
6. 蛮不讲理级数定义法
定义:
\sin x:=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...
\cos x:=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...
所以显然 \sin'x=\cos x
7. 蛮不讲理欧拉公式定义法
定义:
e^z:=1+z+\frac{z^2}{2!}+\frac{z^3}{3!}+...
\sin z:=\frac{e^{iz}-e^{-iz}}{2i}
\cos z:=\frac{e^{iz}+e^{-iz}}{2}
因为 (e^z)'=e^z
所以 \sin'x=\cos x








