两个算符对易，应该怎么去理解？

我在评论区里提到力学量的对易子一般都是纯虚数, 这个结论好像意外地有一部分人没听过?

其实吧, 更严格一点的说法是厄米算符对易子一定是反厄米的, 这不是啥经验之谈, 可以轻松证明:

\[\begin{align} & \ \ \ \ \ \ \ \text{set}\ H_{1}^{\dagger }={{H}_{1}},H_{2}^{\dagger }={{H}_{2}} \\ & \Rightarrow {{\left[ {{H}_{1}},{{H}_{2}} \right]}^{\dagger }}={{\left( {{H}_{1}}{{H}_{2}} \right)}^{\dagger }}-{{\left( {{H}_{2}}{{H}_{1}} \right)}^{\dagger }}={{H}_{2}}{{H}_{1}}-{{H}_{1}}{{H}_{2}}=-{{\left[ {{H}_{1}},{{H}_{2}} \right]}^{\dagger }} \\ & \Rightarrow \left[ {{H}_{1}},{{H}_{2}} \right]\ \text{is}\ \text{an}\ \text{anti-hermitian}\ \text{stuff}\text{.}\ \\ \end{align}\]

看 tag 都是物理方向的, 那么我这里总结一下从量子力学角度的理解:

我们都知道任意两个算符 A,B 的测量具有不确定性关系 \[\Delta A\Delta B\ge \frac{1}{2}\left| \left\langle \left[ A,B \right] \right\rangle \right|\]

所以当我们看到两个算符可对易的时, 我们想到的应该是二者对应的物理量可以同时被精准测量. ^[1]

这等价于说存在一些量子态即是 A 的本征态又是 B 的本征态.

一般而言我们研究的都是厄米算符, 所以更进一步来说就是:

"如果两个厄米算符 A 与 B 对易, 则 A 与 B 的共同本征矢构成态空间的一个正交归一基. "

厄米算符的本征矢本来就有完备性, 即这个命题重点在于:

\[\left[ A,B \right]=0\Rightarrow \] 二者存在一组共同的本征矢.

结论的证明:

设 \[A\left| u_{n}^{i} \right\rangle ={{a}_{n}}\left| u_{n}^{i} \right\rangle \ \ \ i=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] 其中 i 用于区分同本征值子空间各基矢.

A 是厄米算符 \[\Rightarrow \left\langle u_{n}^{i}|u_{m}^{j} \right\rangle ={{\delta }_{mn}}{{\delta }_{ij}}\] ----------------------------------------------[i]

\[\left[ A,B \right]=0\Rightarrow AB\left| u_{n}^{i} \right\rangle =BA\left| u_{n}^{i} \right\rangle ={{a}_{n}}B\left| u_{n}^{i} \right\rangle \]

说明 \[B\left| u_{n}^{i} \right\rangle \] 也是 A 的本征矢, 且处于 \[{{a}_{n}}\] 对应的本征子空间 ^[2] ------------------------[ii]

下面讨论在 A 的本征矢表象下的 B 矩阵 (即 B 的矩阵元 \[B_{mn}^{ij}=\langle u_{m}^{i}|B\left| u_{n}^{j} \right\rangle \] ):

(不懂矩阵表示的看这 正樹：表象变换的幺正算符怎么定义的? 为何说算符与态可以看作矩阵?)

结合 [i][ii] 不难得到: \[m\ne n\Rightarrow B_{mn}^{ij}=\langle u_{m}^{i}|B\left| u_{n}^{j} \right\rangle =0\]

这说明 B 是一个分块对角的矩阵:

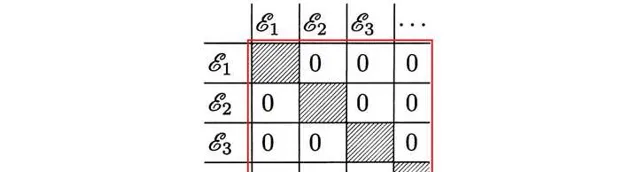
其中 \[{{\varepsilon }_{n}}\] 代表 \[{{a}_{n}}\] 的本征子空间即 \[\left| u_{n}^{i} \right\rangle \ \ \ i=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] 张成的空间.

而阴影部分就是我们接下来要讨论的部分了:

(1). 若 A 的本征值非简并, 即 \[{{g}_{n}}\equiv 1\] , 每个格子都是\[1\times 1\] 的矩阵, 这就说明上面这个矩阵就是个对角阵. 此时标注简并情况的 i 可以去掉, \[\left| u_{n}^{i} \right\rangle =\left| {{u}_{n}} \right\rangle \] 就是 \[B\] 的本征矢.

(2). 若 A 的本征值存在简并, 则图中的每个阴影子块都是一个 \[{{g}_{n}}\times {{g}_{n}}\] 的方阵, 其中的矩阵元表示为 \[B_{nn}^{ij}=\langle u_{n}^{i}|B\left| u_{n}^{j} \right\rangle \] 其中 \[i,j=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] . B 是厄米算符, 所以这个子块也是厄米矩阵, (即 \[{{\left( B_{nn}^{ji} \right)}^{*}}=B_{nn}^{ij}\] ), 这说明这个矩阵一定可以对角化, 对角化的过程无非就是在子空间内寻找一组新的矢量做基使得这组基中表示的 B 矩阵是对角阵. 仿照 (1) 中的过程不难发现所有的新矢量都是 B 在 \[{{\varepsilon }_{n}}\] 中的本征矢. 各个子空间中的所有新矢量的集合即为所求的一组完备的共同本征矢, 即这些新矢量同时是 A 与 B 的本征矢.

♦\text {Q:} 前面说了若 A 与 B 可对易, 就可以找到一组共同的本征矢, 那么难道不可对易就一定不能找到一组共同的本征矢吗？

♦\text {A:} 是的,下面用反证法予以证明:

假定算符 A 与 B 不可对易. 但我就是 somehow 找到了他们的一组共同本征矢 \[\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 使得 \[A\left| {{a}_{n}},{{b}_{n}},i \right\rangle ={{a}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 且 \[B\left| {{a}_{n}},{{b}_{n}},i \right\rangle ={{b}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 其中 i 标注简并情况.

那么就有 \[\left( AB-BA \right)\left| {{a}_{n}},{{b}_{n}},i \right\rangle =AB\left| {{a}_{n}},{{b}_{n}},i \right\rangle -BA\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] \[\begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =A{{b}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle -B{{a}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\left( {{a}_{n}}{{b}_{n}}-{{b}_{n}}{{a}_{n}} \right)\left| {{a}_{n}},{{b}_{n}},i \right\rangle =0 \\ \end{align}\]

由于 \[\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 不能全是零矢量, 所以只能是 \[AB-BA=\left[ A,B \right]=0\]

这就与前提矛盾了, 所以, 你不能.

我们一般利用这个特性来构造可对易观察算符的完全集合 ^[3] .

如果觉得上面那些实在有些抽象心里没底的话可以看看下面这个:

参考

1. ^ 如果有对应的物理量的话
2. ^ 厄米阵的不同本征子空间都是相互正交的.
3. ^ 有些地方称之为力学量完全集