问题相对来说没有那么复杂,题主可以有多种方式来获得1.5 I_{r} 或其他电流倍数下的脱扣时间。
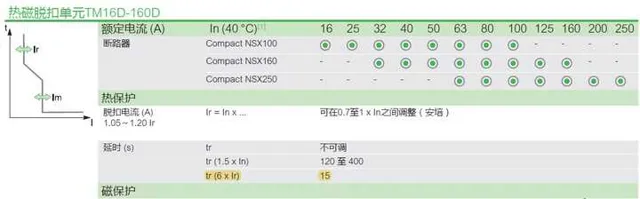
我们以施耐德热磁式塑壳断路器NSX250TMD为例,TMD是热磁式配电脱扣器的代号--Thermal Magnetic Distribution。图1 是NSX250TMD断路器长延时保护(热保护)和短路保护(磁保护)的整定界面, I_{r} 就是热保护整定电流,对于热磁式断路器 I_{r} 可以整定为0.7~1.0倍 I_{n} ( I_{n} 为断路器额定电流),例如对于NSX250TMD,热保护整定电流范围为:175A~250A。 I_{m} 为磁保护整定值,对于NSX250TMD其磁保护整定可以选择5~10 I_{n} 。

对于热磁式断路器,其长延时保护的延时时间 t_{r} 一般不可调(电子式可以调),延时时间调整在曲线上的差别如图2和图3, 6I_{r} @ t_{r} 决定了长延时(热保护)曲线的走向 , t_{r} 选择越小,意味着不光6I_{r} 对应的脱扣时间短,长延时保护曲线上其他电流倍数下的脱扣时间也会变短。
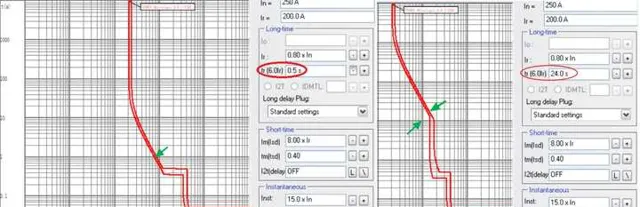
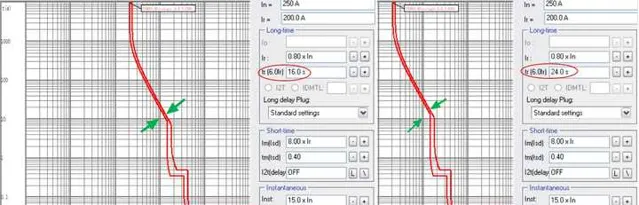
长延时保护(热保护)曲线上时间与电流平方的关系可以认为是常数 I^{2}t=K (图4), 如果已知6 I_{r} @ t_{r} ,就可以理论计算长延时保护曲线上任意电流倍数下的脱扣时间。 例如已知6I_{r} 的脱扣时间为24s,那么3 I_{r} 时的脱扣时间大致为96s(未考虑误差),其他电流倍数可以自行计算。
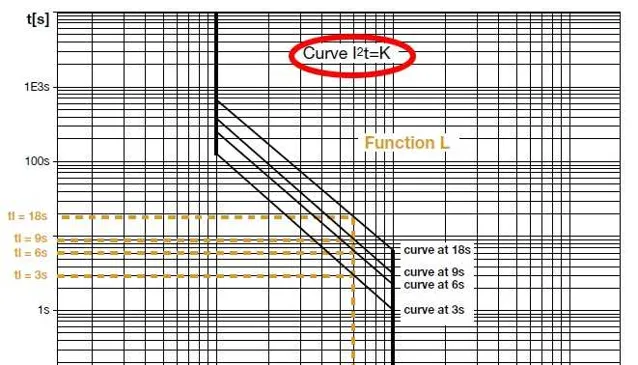
对于NSX250TMD断路器,其6 I_{r} 对应的时间只有15s这一档(图5),题主想知道1.5I_{r} 时的脱扣时间,其实样本里已经给出,时间范围为120~400s。我们按 I^{2}t=K 计算的理论脱扣时间大概为240s(未考虑误差)。