能科普下随机图理论吗？

随机图模型

随机图的历史

在 1959 和 1968 年期间，数学家 Paul Erdos 和 Alfred Renyi 发表了关于随机图（ Random Graph ）的一系列论文，在图论的研究中融入了组合数学和概率论，建立了一个全新的数学领域分支---随机图论。

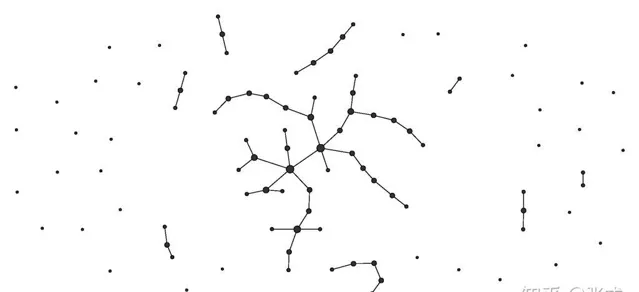
随机图的定义

本文只关注无向图的场景。顾名思义， 随机图（Random Graph） 就是将一堆顶点随机的连接上边。好比在地上撒了一堆豆子，而豆子之间是否用线来相连是根据某个概率值来确定的。通常来说，对于随机图而言有两种定义方式

1. 【定义一】给定 N 和 M, G_{1}(N,M) 的定义是随机从 N 个顶点和 M 条边所生成的所有图集合中选择一个。其中，这样的图集合的势是 C(N(N-1)/2, M), 因此获得其中某一个图的概率是 1/C(N(N-1)/2, M).
2. 【定义二】给定 N 和 p ， G_{2}(N,p) 的定义是有 N 个顶点，并且两个顶点之间以概率 p\in[0,1] 来决定是否连边。

事实上，这两个定义是等价的， N 个顶点的图最多拥有的边数是 N(N-1)/2, 而 G_{1}(N,M) 恰好有 M 条边，并且它们分配的概率是均等的，因此两个顶点之间是否存在边的概率就是 p = M/(N(N-1)/2), 这里的 C 指的是组合数。i.e.

G_{1}(N,M) = G_{2}(N, \frac{M}{N(N-1)/2}).

另一方面，对于 G_{2}(N,p) 而言，顶点两两之间是否存在边的概率是 p, 而 N 个顶点的图最多拥有 N(N-1)/2 条边，于是边数为 pN(N-1)/2. i.e.

G_{2}(N,p)=G_{1}(N,pN(N-1)/2).

进一步地，通过以上两个公式可以得到：

G_{1}(N,M)=G_{2}(N,\frac{M}{N(N-1)/2}) = G_{1}(N,M).

在定义一中，可以直接算出所有顶点的平均度是 \langle k\rangle = 2 M /N. 但如果要计算图的其余指标，用第二种定义 G_{2}(N,p) 反而更加容易，因此后续将会重点关注第二种定义，为方便起见，记号简化为 G(N,p) = G_{2}(N,p).

随机图的度

图的 度（degree） 指的是对于某个顶点而言，与它相关联的边的条数。对于随机图 G(N,p) 而言，它的边数大约是 pN(N-1)/2, 最多与该节点相连接的顶点数为 N-1, 整个图的顶点平均度是（边数 * 2) / 顶点数，用记号 \langle k\rangle 来表示，意味着顶点平均度是 \langle k\rangle = p(N-1) \sim pN, 当 N 充分大的时候成立。换言之，

p \sim \langle k\rangle / N.

对于随机图 G(N,p) 中的一个顶点 i 而言，我们想计算它恰好有 d 条边的概率值。事实上，对于除了 i 之外的 N-1 个点而言，有 d 个顶点与 i 相连， N-1-d 个顶点与 i 不相连，其概率是 p^{d}(1-p)^{N-1-d}, 同时需要从这 N-1 个点中选择 d 个点，因此，顶点 i 的度恰好是 d 的概率是

p_{d}=C(N-1, d)\cdot p^{d}\cdot (1-p)^{N-1-d}.

特别地，当 d\ll N 时，上述概率近似于泊松分布（Possion Distribution）。事实上， p=\langle k\rangle / (N-1) 并且

C(N-1,d) = (N-1)(N-2)\cdots(N-d+1)/ d! \sim (N-1)^{d} / d!,

(1-p)^{N-1-d} \sim (1-\langle k\rangle /(N-1))^{N-1-d} \sim e^{-\langle k\rangle},

因此，在 d\ll N 时， p_{d} 近似于泊松分布，

p_{d} \sim \langle k\rangle^{d}e^{-\langle k\rangle}/d!.

随机图的连通分支

对于随机图 G(N, p) 而言，它的连通分支个数是与顶点的平均度 \langle k\rangle 息息相关的。特别地，当 \langle k\rangle=0 时，每个顶点都是孤立的，连通分支个数为 N; 当 \langle k\rangle=N-1 时，任意两个顶点都有边相连接，整个图是完全图，连通分支的个数是 1. 顶点的平均度从 0 到 N-1 的过程中，连通分支的个数从 N 演变到 1, 最大连通分支顶点数从 1 演变到 N, 那么在这个变化的过程中，最大连通分支的顶点数究竟是怎样变化的呢？是否存在一些临界点呢？数学家 Erdos 和 Renyi 在 1959 年的论文中给出了答案：

对于随机图 G(N,p) 而言，用 N_{G} 表示最大连通分支的顶点个数，那么对于图的平均度 \langle k\rangle 而言，

1. 当 \langle k\rangle = Np < 1, 那么 N_{G} = O(\ln(N));
2. 当 \langle k\rangle = Np = 1, 那么 N_{G} = O(N^{2/3});
3. 当 \langle k\rangle = Np \in (1, \ln(N)), 那么巨连通分支（Giant Component）存在，同时存在很多小的连通分支，在临界点 1 的附近时， N_{G} \sim (p-p_{c})N, 这里 p_{c}=1/N;
4. 当 \langle k\rangle = Np \in (\ln(N),+\infty), 那么图 G 是全连通图，i.e. N_{G}=N.

在这个定理中，对于顶点的平均度 \langle k\rangle 而言，存在两个临界点，分别是 1 和 \ln(N). 当 \langle k\rangle < 1 时，巨连通分支不存在，所有连通分支的量级都在 O(\ln(N)) 以下；当 \langle k\rangle = 1 时，巨连通分支开始出现，量级大约是 O(N^{2/3}); 当 1<\langle k\rangle <\ln(N) 时，随机图存在一个巨连通分支和很多小的连通分支；当 \langle k\rangle > \ln(N) 时，图是连通图。

整个定理的证明有点复杂，但本文将会介绍 两个临界点 的计算。先来考虑第一个临界点 \langle k\rangle = 1 的情况：

用 N_{G} 来表示随机图 G 中的最大连通分支的顶点个数， u 表示图 G 中不在最大连通分支的顶点比例，i.e.

u=(N-N_{G})/N = 1 - N_{G}/N= 图的顶点不在最大连通分支的概率。

对于不在最大连通分支的顶点 i 而言，其余的 N-1 个顶点分成两种情况，Case（1）：要么 i 与之不相连，此时概率是 1-p; Case（2）：要么 i 与之相连，但此时的顶点不能在最大连通分支中，那就只能在剩下的 uN 个顶点中，其概率是 pu. 于是，对于所有顶点而言，它不在最大连通分支的概率是 (1-p+pu)^{N-1}. 于是，

u=(1-p+pu)^{N-1}=(1-p(1-u))^{N-1}.

根据 p\sim\langle k\rangle /N 和 \lim_{N\rightarrow +\infty}(1+x/N)^{N}=e^{x} 可以得到当 N 充分大时，有

u = (1-p(1-u))^{N-1} = (1-(1-u)\langle k\rangle /N)^{N-1} \sim e^{-(1-u)\langle k\rangle}.

令 s= 1-u = N_{G}/N, 它表示最大连通分支的顶点个数在所有顶点个数的占比，从而可以得到 近似方程 ：

1-s=e^{-\langle k\rangle s}.

令 g(s) = 1 - s - e^{-\langle k\rangle s}, 则 g(0) = 0, g(1) = -e^{\langle k\rangle}<0. 它的导数是 g'(s) = - 1 + \langle k\rangle e^{-\langle k\rangle s}, 通过计算可以得到：

1. 当 \langle k\rangle \leq 1 时， g'(s)<0 在 (0,1) 上成立，i.e. g(s) = 0 在 [0,1] 上的唯一解是 s=0, 换言之， N_{G}/N = s \rightarrow 0;
2. 当 \langle k\rangle > 1 时，g'(s)>0 在 (0,\ln\langle k\rangle/\langle k\rangle) 成立， g'(s)<0 在 (\ln\langle k\rangle /\langle k\rangle,1) 成立。换言之， g(s)=0 在 [0,1] 上除了零之外还有解 s_{0}\in(0,1). 此时会存在巨连通分支， N_{G}/N = s_{0}\in (0,1) 是解。

因此，最大连通分支的顶点数在这个点会出现突变， 1 是该方程的第一个临界点，并且是出现巨连通分支的临界点。

再来考虑第二个临界点 \langle k\rangle = \ln(N) 的情况。对于极限状况而言，假设仅有一个顶点不在最大连通分支中，那么 s = N_{G}/N = (N-1)/N, 此刻，

1/N=1-s=e^{-\langle k\rangle s}=e^{-\langle k\rangle (N-1)/N},

两边求对数可以得到 \langle k\rangle = \ln(N), 因此，\ln(N) 也是一个临界点，并且是出现全连通图的临界点。

随机图的六度分离

六度分离 又称为 小世界现象 ，它的含义是在地球上任意选择两个人，他们之间最多相隔 6 个相识关系。换言之，来自世界上任何地方的两个人都可以通过不超过 6 个相识关系所连接起来。

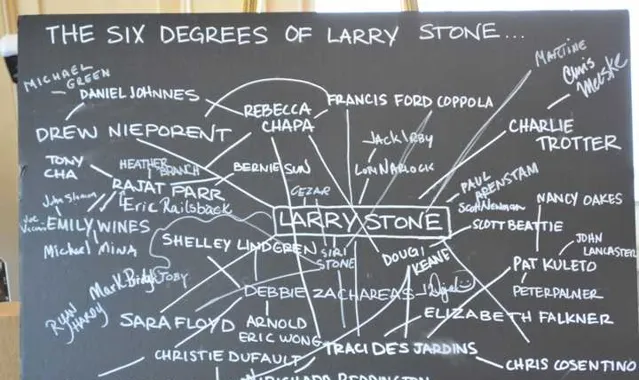
图中两个顶点的距离定义为两个顶点之间的最短路径长度，图的直径就是图中任意两点的距离的最大值。对于随机图 G(N,p) 而言，如果 \langle k\rangle \leq 1 则是不连通的，因此通常只需要考虑 \langle k\rangle>1 的情况，甚至只考虑 \langle k\rangle >\ln(N) 的全连通图。任取一个顶点 i ，则有

1. \langle k\rangle 个距离为 1 的顶点；
2. \langle k\rangle^{2} 个距离为 2 的顶点；
3. \langle k\rangle^{3} 个距离为 3 的顶点；
4. \langle k\rangle^{d_{max}} 个距离为 d_{max} 的顶点；

同时，G(N,p) 而言，顶点的个数为 N, 这意味着 \langle k\rangle + \langle k\rangle^{2}+\cdots+\langle k\rangle^{d_{max}}\leq N. 通过等比级数的公式可以得到 \langle k\rangle^{d_{max}} \leq N, 因此，

d_{max} = O(\ln(N)/\ln(\langle k\rangle)).

而随机图的直径的量级是与 d_{max} 成正比的，因此，随机图的直径量级同样是 O(\ln(N)/\ln(\langle k\rangle)). 如果 N = 10^9 并且每个人认识 \langle k\rangle = 200 个人，于是随机图的直径量级是 \ln(6*10^9) / \ln(200) = 4.25 < 6.

参考文献

1. Erdos Renyi Model：https:// en.wikipedia.org/wiki/E rdős–Rényi_model
2. Giant Component：https:// en.wikipedia.org/wiki/G iant_component
3. Erdős P, Rényi A. On the evolution of random graphs[J]. Publ. Math. Inst. Hung. Acad. Sci, 1960, 5(1): 17-60.
4. Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Reviews of modern physics, 2002, 74(1): 47.
5. 【巴拉巴西网络科学】，艾伯特-拉斯洛·巴拉巴西（Albert-LászlóBarabási），2020.