照本宣科一番。看回答的同志们能不能多发几个评论?提出疑问或者指出错误都行,我希望能跟大家多讨论讨论。这几天点赞喜欢收藏比我之前的回答都多,结果只有一条评论。。。。
首先声明:本回答 不是我自己推导 的,仅仅选择性 转述了李俊清老师在中国科学技术大学出版的【物质结构导论】第三章中的部分内容 。我也是借此机会复习一下在我看来量子化学中对于有机化学专业学生最具有启发和理论支撑价值的一部分内容。我个人数学功底不是很好,所以在接触这些推导过程的时候喜欢联系一些化学图像来辅助理解。我把这些 自己的体会和思考,以及一些自己犯过的错误、有偏差的想法都补充在推导过程旁边 ,希望可以对跟我一样不擅长数学的同学有所帮助。 【物质结构导论】 这本书比较老了,可能不太好找。也可以参考Ira N. Levine的【Quantum Chemistry 7th Edition】(Pearson, 2012; ISBN-13: 978-0-321-80345-0)Chapter 13。推导过程是基本一样的。我个人强烈推荐用这两本书学习量子化学。前者数学推导基本严格但不是太繁琐,论证简洁,适合新手上手。后者我打算过年再看一遍重新学习一下。
重申一遍:我数学确实不太好,所以下面的 过程可能不严谨,欢迎大家批评指正 。我绝对没有说数学不重要的意思,而且我觉得良好的数学基础对于学好量子化学是很巨大很巨大很巨大的助力。但是如果一些同学和我一样实在没有能力自己独立地推导某些积分或者变形过程,我觉得问题也不是很大。但是,我们必须要意识到我们做一切数学工作的目标是什么。只要紧扣解决问题的策略,我们就可以理解大部分数学变化的动机,以及某些近似成立的原则和带来的问题。这些理解是很重要的。如果你不用应付考试,你甚至可以不记住某些公式的具体形式;但是我们应该做到看到某个公式就能明白它所描述的物理图像。
本回答旨在通过简化的线性变分法解p+氢分子离子的薛定谔方程来解释分子轨道中成键反键的由来。我们应该首先认识到:所谓成键和反键只是结果,是电子填充到能量不同的轨道上造成的分子结构变化。它的产生原因比较难以用经典力学解释,或者用宏观世界的模型来类比。
先厘清一些基本观念:在量子化学的框架下,任何一个原子核和电子构成的体系(比如原子、分子)都可以用一个薛定谔方程来描述;它们的形式会随着构成元素的不同而变化(比如核的数量、核电荷数、电子数量等)。薛定谔方程是一个偏微分方程,它的解是一个(组)函数( Ψ1,Ψ2,Ψ3.... ),这些函数被称为波函数。通常,当体系较为复杂时薛定谔方程没有严格解析解;比如氢气,这就已经很复杂了,我们一般不会去求氢气分子薛定谔方程的解析解。但是,我们有很多方法用近似手段来简化求解过程,而且实验证明这些近似方法的结果是很精确的。
一种极其常用的近似思路是:我们可以利用 可严格求解的原子轨道 来拟合一个 分子轨道 。这里所谓「轨道」,其本质某个体系薛定谔方程的波函数 Ψ 。它的数学基础是:原子轨道薛定谔方程的解(波函数)构成一个完备的集合,即它们的线性组合(如式4)能够构成所有复函数。我们把分子轨道分解成原子轨道线性组合的形式之后,就可以作进一步的简化,并且套用一些原子轨道的现成结论。所谓的成键轨道和反键轨道,就是一个给定分子体系薛定谔方程的 某一组的两个解 ;它们均满足薛定谔方程,但能量本征值不同。
薛定谔方程和它的解究竟可以怎样描述分子体系呢?首先,波函数本身没有明确的物理意义,但对它做算符作用可以求解体系的能量(如式###);而所谓的电子云,本质是一个概率密度函数,而且它和波函数的关系是:
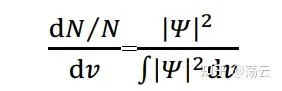
上式左侧表示体积微元d v 中出现粒子的数量与总粒子数之比,即「概率密度」。右侧分母对于标准化的波函数为1。而右侧的分子「绝对值的平方」的展开形式为:
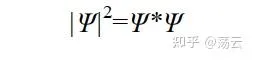
之所以写成 Ψ* · Ψ (前面的函数加*表示其共轭复函数),是因为波函数 Ψ 是一个含有复变量的函数。
没学过复变函数的同学不必纠结这些数学,这不是重点。你只需要知道以下两点:
- 一个分子体系可以由薛定谔方程描述,它的解是波函数,反映了分子的性质,至少包含以下两方面的物理意义:(1)波函数的平方是概率密度函数,就是体系电子云的分步。(2)波函数可以通过算符作用表示体系的能量。
- 由于薛定谔方程通常难以精确求出解析解,所以我们要做近似和简化。具体的方法是,首先假定分子薛定谔方程的解(分子轨道)可以写成原子轨道线性组合的形式(而且事实上这在数学上是严密的)。稍后我们会介绍如何进行这种操作,以及它为什么可以简化计算。
好了,上面这些只是提供一点基本认识框架,简单地介绍了我们的任务和解决问题的基本策略,避免没有基础的同学对下方推导中进行某些变换的动机提出疑问。以下开始正式推导。
对于氢分子离子p+,即两个质子一个电子构成的体系,如图:
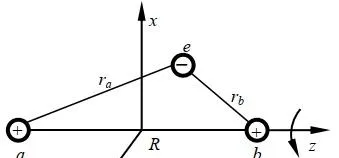
该模型中的成键,即电子结构可由电子波函数和能量描述。问题归结为解这个体系的 Schrödinger 方程 。 Ψ 为体系波函数。
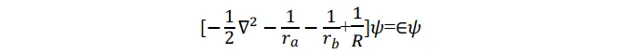
这个方程在椭球坐标系下可以精确求解, 但是多电子分子的 Schrödinger 方程都不能严格求解,所以该方程的精确求解没有普遍性。下面用 线性变分法 近似 求解该方程。
对于在基态下的 p+,如果电子在氢核 a 附近运动,即 ra<<rb,ra<<R,则方程可近似地写为
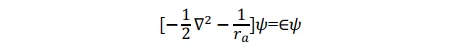
其形式满足氢原子a的Schrödinger 方程,其基态即为氢原子1s态。同理,当p+的电子在氢核 b 附近运动时,其基态也是氢原子的 1s 态。所以1sa和1sb两个原子轨道函数应均满足上述薛定谔方程。当电子分别在a核和b核附近运动时,应分别有:(本段的说法我个人感觉不太完善,欢迎大佬补充更好的解释)
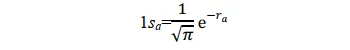
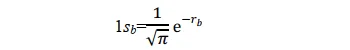
当p+的电子在其它区间运动时,其基态应不同于 1sa 或 1sb;但应与 1sa 或 1sb 有关,因为至少在电子分别靠近两个核时的特殊情况下, Ψ 可以别近似为 1sa 或 1sb 作为粗糙的近似,可以把 Ψ 表示为 1sa 和 1sb 线性组合。
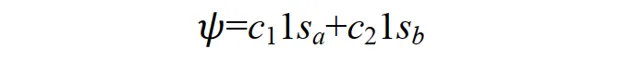
这种近似称为分子轨道表示为原子轨道的线性组合,简称 LCAO 近似 (linear combination of atomic orbitals)。在原子结合成分子的过程中,电子运动波函数一般有较大的形变.如果像上式那样仅用两个原子轨道的线性组合来表示分子轨道,显然是很粗糙的.为了提高精确度,应该用大量的原子轨道的线性组合来表示分子轨道 Ψ 。如开始的介绍中所说,我们用大量原子轨道定态方程的解(原子轨道)为基函数拟合出了一个较精确的分子薛定谔方程解(分子轨道)。其中组合系数 c1, c2, …可由变分法求得。因这种变分法的参数是线性组合系数,故称为线性变分法。
如果每一个原子轨道都是其对应的 Schrödinger 方程的精确解,则通常所有这些精确解构成一个完备系。下式的展开式中若包括无限多个原子轨道,则它所表示的分子轨道可以达到数学上严格精确的程度。在实际应用中,一般只取有限个原子轨道的线性组合,即LCAO近似。(关于变分法可以参考Levine书的第8章,讲的非常好,虽然是英文的但很容易理解)
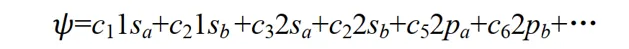
对于一个特定的分子轨道,展开式(4)中只有少数几个原子轨道的贡献是主要的。例如 CO 分子的一个占据电子的成键分子轨道,主要应由碳和氧原子的 2s 和 2p 轨道组合而成,其它原子轨道,如 1s, 3s,3p, 3d, 4s 等轨道对 CO 的成键贡献应该是很小的。为了定性地讨论问题,仅用碳和氧的 2s 和 2p 轨道组合起来,也许就能反映出 CO 成键的主要特征。同样,对氢分子离子p+,对其共价键起主要作用的是氢原子的 1s 轨道,可以用两个氢原子的 1s 轨道线性组合式(3)来定性地讨论p+的成键问题。
这里不厌其烦地弱弱插一句:线性组合,在元函数足够多(直到构成相互正交完备集)的时候是趋近于严格精确的。只用两个轨道的近似在数学上是非常粗暴不合理的,但事实证明这种简陋的模型与实验事实吻合得很好。一方面大大简化了分析复杂度,一方面对讨论问题的结论影响不大,因此这种方法很受欢迎。以后大家还会见到更粗暴的近似,没错,说的就是你HMO(休克尔分子轨道法)。
定义(1)中的Hamiltonian(哈密顿算符)为
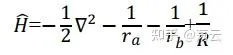
则(1)可转化为
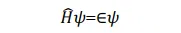
上式左乘 Ψ* 并对整个空间积分,得
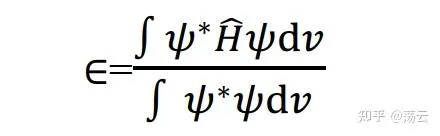
将(3)代入上式,则有
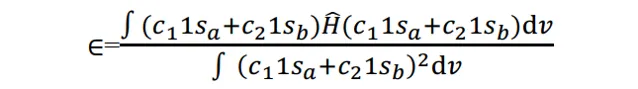
式(6)描述了这个体系的能量。我们要对它 做变分 , 使体系能量最低 ,求出各个组合系数c的值。
我们先把式(6)简化一下,可定义以下四式。四个式子中,第一个和第四个是由于a核和b核是完全等价、可以互换的,所以能够成立;第二三个是因为哈密顿算符的厄米性所以能够成立(关于厄米性[Hermite]请参阅Levine书第7章)。
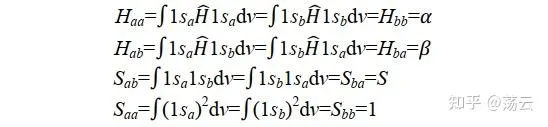
代入到(6)中
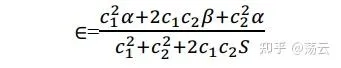
下面,按照变分原理,能量值最小时必须有
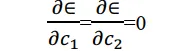
把(7)代入上式得到
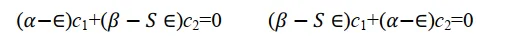
关于c1和c2的二元一次方程组(8)有非零解的条件是系数行列式为零。 这是一个必须加入的附加条件。 上面这个方程组出现0解即代表它对应的原子轨道不参与分子轨道组合,其权重为0,不符合问题的数学设定,也不符合物理。
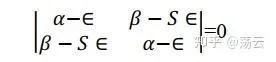
这个方程称为久期方程,因其与描述行星的久期运动的方程相似而得名。解得
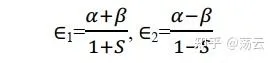
我们通过 解不为零 的性质拿到了最低能量可能值,现在回代方程组(8)得到 c1=c2。
再加上一个附加条件:归一化,即概率密度函数对全空间的积分必须等于1:
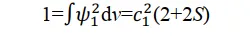
解出

所以首先解出 Ψ1,同理可解出Ψ2:
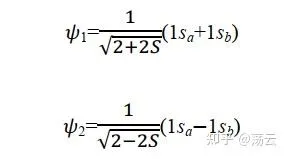
好的,现在我们已经取得了阶段性的重要胜利:拿到了分子轨道波函数的具体(近似)形式。可以小结一下:氢分子离子是共价键的一个简化模型,在其中不用考虑 电子互斥、自旋和全同性 的问题,只需要考虑两个质子正电荷和一个电子构成的简单系统中三者之间的相互作用。列出薛定谔方程后,我们用LCAO近似的方法,首先将薛定谔方程的解写成原子轨道线性组合的方式,然后通过变分法求得组合系数,同时得到了两个能量值和两个分子轨道,即电子在整个分子体系中运动的波函数。这个过程中需要用到 组合系数不为零 以及 波函数归一化 两个预先设定好的条件。
我们再来看看我们拿到的结果。关于上面定义的 α、β 和 S 三个积分量,可以通过在椭球坐标系中的积分求出。过程比较复杂(老实说作为学化学的我也不会),我就直接放结论:
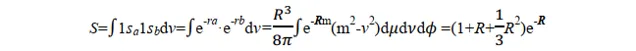
当核间距 R =0 时, S =1;当 R =∞时, S =0;当 0< R <∞时,1> S >0。实验发现在p+的平衡构型下, R e=2 a.u. (a.u.为原子单位,是一个能量单位),由上式可得平衡构型下的 S e=0.586。可见 S 表示两个轨道 1sa 和 1sb 的重迭程度,故 S 称为重迭积分.图 3.2 表示了两个轨道 1sa 和 1sb 的重迭情况和重迭积分的大小.
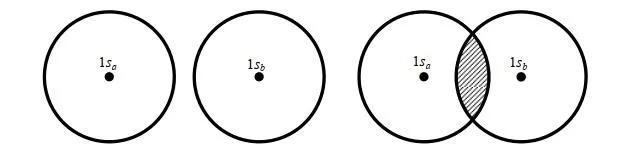
一种常有的错误认识是:原子轨道都是相互正交的,故 S 应恒为零。在这里应强调:只有属于同一个原子的原子轨道才是正交的;属于不同原子的原子轨道,因其不是同一个 Hamiton 算符(是Hermite 算符)的本征函数,故它们并不相互正交。 正是不同原子的原子轨道间的重迭积分 S,才导致了共价键的形成 。(关于哈密顿算符及本征函数、完备函数域请参阅Levine书第7章)
关于α,则有
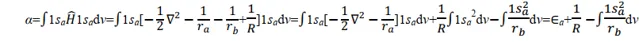
其中 Ea 为孤立的氢原子的基态能量,为 0.5 a.u.。1/ R 为核间排斥能; 在平衡构型下, R = 2a.u.; 1/ R =0.5a.u.。被积函数是1sa 态的电子与核 b 的吸引能。由此可见 α 主要与粒子间的 Coulomb 作用有关,故称 α 为 Coulomb 积分,可用椭上式中积分项得到
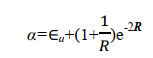
在平衡构型下 R e=2 a.u. ,可得
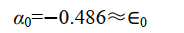
即 Coulomb 积分 α 与原子轨道能量 E a 近似相等
根据较复杂的椭球坐标积分(这里省略具体演算步骤,直接给出结果),可以得到
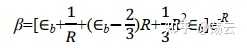
因为 Eb 是基态氢原子b的能量,其值为 -0.5 a.u.;故在平衡构型 R e=2 a.u.,得
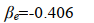
用 S e、 α e和 β e分别代入 E1和E2, 得到平衡构型下的能量为
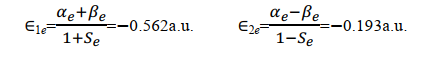
小结一下,通过求解积分值 S 、 α e和 β e我们得到了两种原子轨道线性组合而成的分子轨道的波函数对应的能量本征值。根据式(18), β e为负值,所以式(19)中 E1<E2。注意,这里用的都是原子单位制。
现在我们有了两个波函数,如式(12)
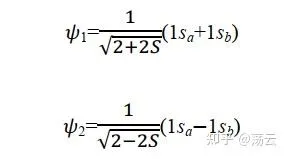
以及他们对应的平衡状态能量
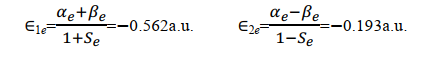
这即是两个分子轨道,一个能量低,一个能量高。它们所描述的电子云概率密度函数为

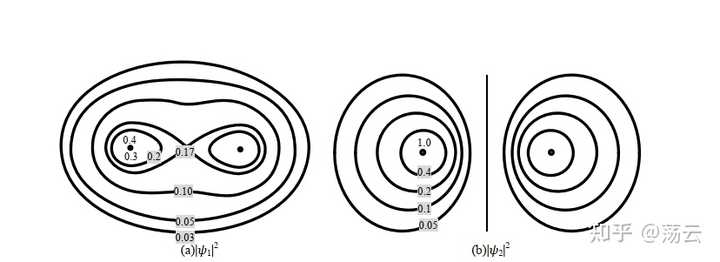
这是两个三维概率密度函数,它们在Z方向的等高线图如上。大家更熟悉的可能是同核sigma成键轨道和反键轨道的图像如下。注意, 这里得到的并不是理论上严谨的分子轨道。 分子轨道法描述分子结构由于需要考虑多电子,还必须引入 Born-Oppenheimer 近似 和 非相对论近似 两个基本近似。下图仅做示例,让大家把此处推导结果和已经学过的模型联系起来。
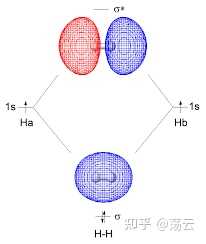
总结关于氢分子离子的讨论,我们可以得到一些定性的结论:两个原子轨道 1sa 和 1sb 的线性组合,可以得到两个分子轨道 Ψ1 和 Ψ2 ,其中一个分子轨道的能量 E 1 低于其原子轨道的能量,这个分子轨道称为成键轨道,另一个分子轨道的能量 E 2 高于其原子轨道的能量,这个分子轨道称为反键分子轨道。在基态时,电子会占据能量低的成键轨道。注意,式(12)中两个波函数的形式,可以视为分别为同相位叠加和不同相位抵消的结果,前面的1/根号部分可以看成一个归一化因子。此外,分析ra=rb的情形就可以直观地看出成键轨道两原子中间的部分概率密度极大,而反键轨道该位置概率密度基本为0,形成节点。
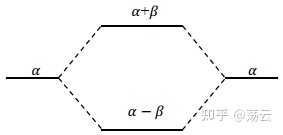
可以把这个结论用能级图直观地表示出来.在平衡构型下, Coulomb 积分 α 近似地等于氢原子轨道能量 E a(或 E a),所以可用 α 表示原子轨道的能量,作为定性的直观图形表示,可忽略重迭积分 S。成键轨道能量和反键轨道能量分别为
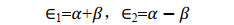
交换积分 β 小于零,所以能级图应如下。两边为原子轨道的能级 α 中间为分子轨道的能级 E1 和 E2。 所谓成键三原则: 能量相近、最大重迭 和 对称性匹配 中的前两个根据上面的推导其实可以进行简单直观的数学解释。最后一个对称性匹配的问题需要借助一点群论的知识。虽然直观看很简单,但要给出一个可靠的普适性的解释其实还是比较麻烦的。但这又是有机化学中重要的HMO(Huckel分子轨道法)的基础。
到此为止,分子轨道的基本推理方法已经简单演示完了。应该基本可以比较严谨地回答题主的问题了。要用浅显的话讲明白一个这种包含大量数学推导的知识和理论好难啊。。。。
以后有空再更新多电子体系分子轨道的理论假设和电子填充规则。











