今天是2022年2月18日,引力子还没有被发现,所以我们还可以说,引力的本质就是时空的扭曲。在现代引力理论中,「引力」恰恰不是一种「力」,这和初高中阶段我们学习的所有东西是矛盾的。
我们先思考一下引力的效果,比如绕着一颗恒星运动的天体,究竟是为什么会绕着恒星转动的?在高中阶段,我们的解释是,这个天体受到了恒星的吸引,吸引力提供了向心力,所以天体会做圆周运动。如果我们没有了「引力」这个概念,这个问题该如何解释?
我们来看看弯曲时空中物体的运动方程:
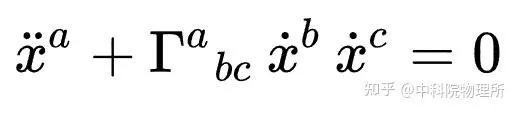
x是(四维)坐标,脑袋上加两个点的是(四维)加速度,加一个点的是(四维)速度。如果 \Gamma 那一项为0,那么天体的加速度就为0,和不受力的物体完全一样。对于做圆周运动的天体来说,我们可以说 \Gamma 项让天体有了加速度——这玩意儿不就妥妥的是「引力」吗,它起到了引力的效果。只不过在不使用广义相对论的情况下这个方程的\Gamma 项长成另一个样子( F = GMm/r^{2} )而已。
这个\Gamma 叫仿射联络(听起来是一个很酷炫的名字),它描述了矢量应该如何被平移。例如下图1中的,是一个平直时空中的平移,而图2则描述了是圆面上的平移。
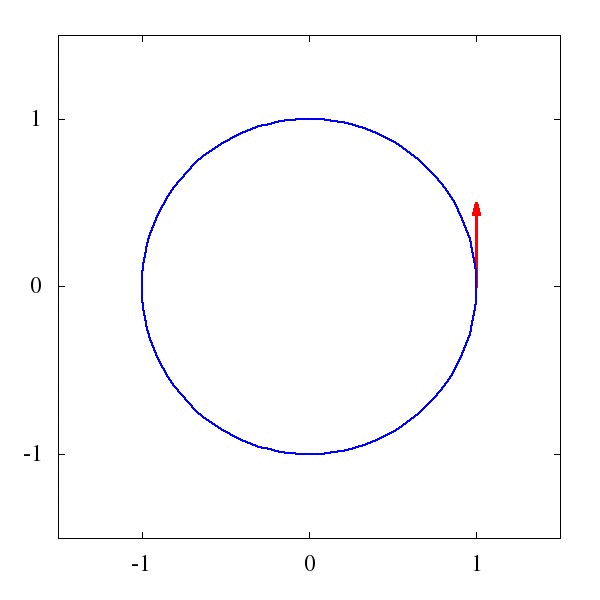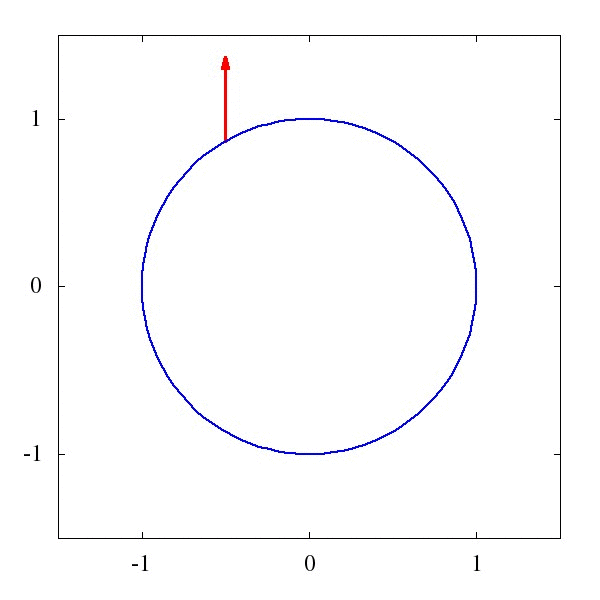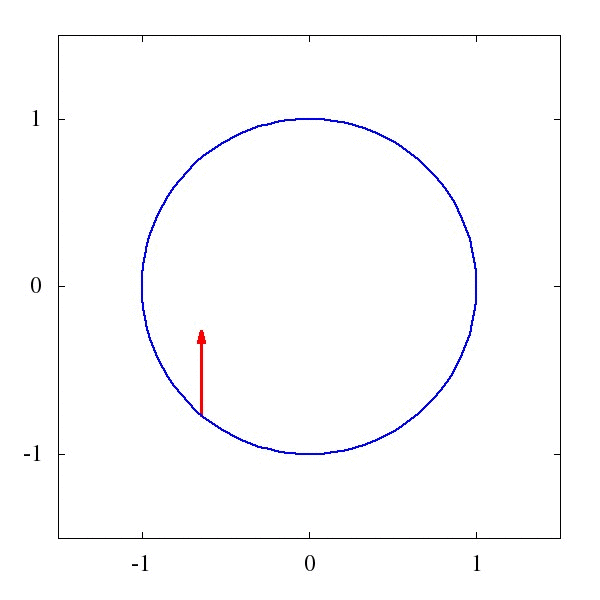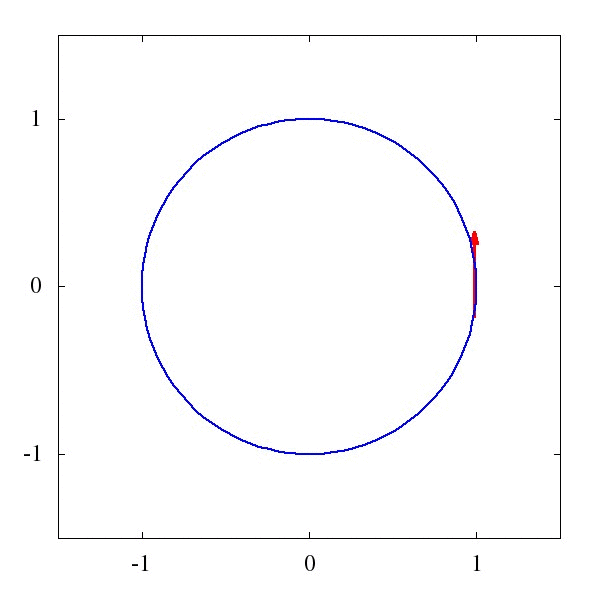
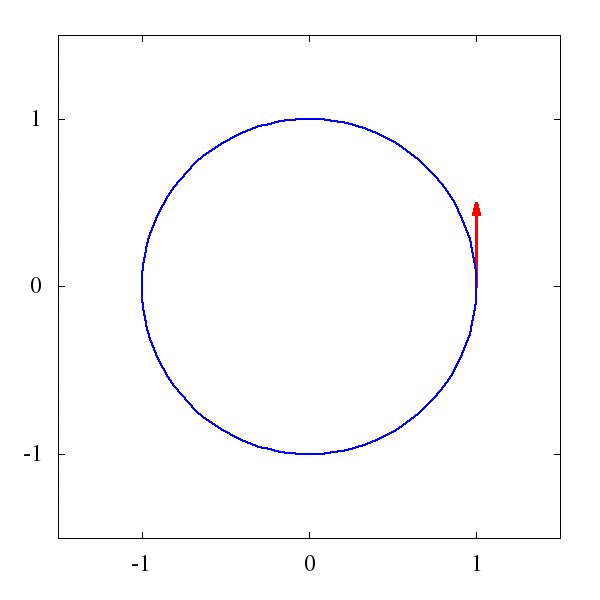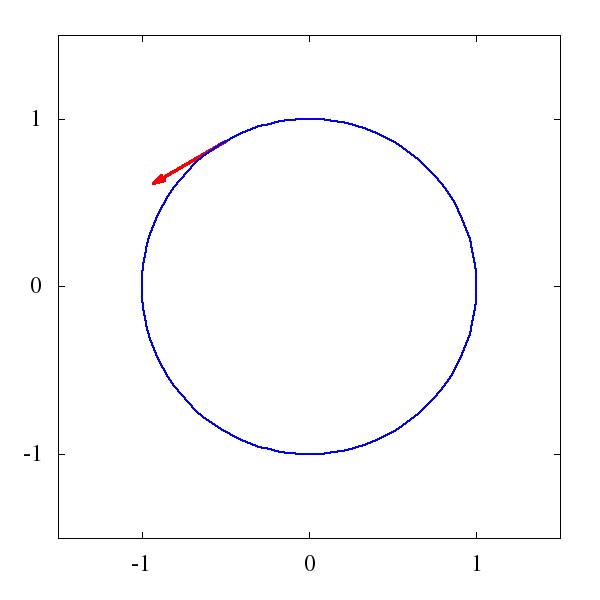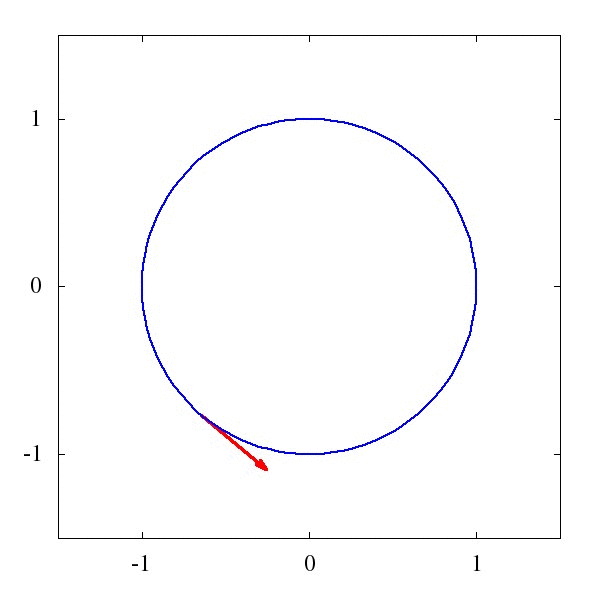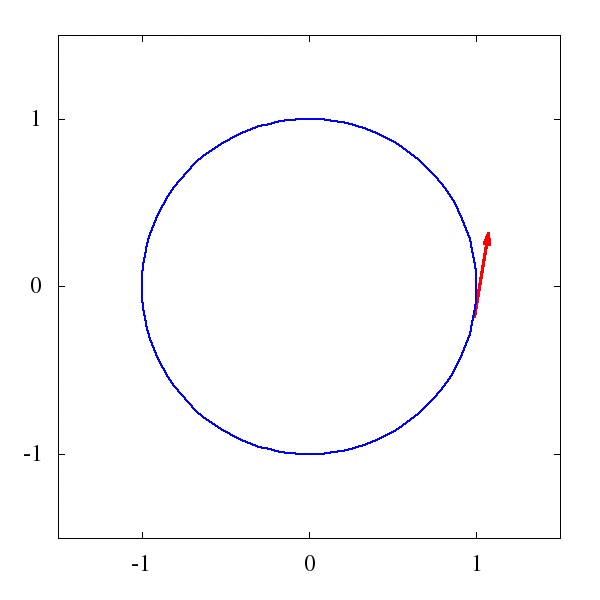
粗略地说,对于均匀平直的坐标系,这玩意儿等于0,而对于弯曲的时空和坐标系,比如篮球的表面吧,这玩意儿就不为0。某种程度上我们可以说,这个仿射联络,就是引力的效应。
那么这个仿射联络是怎么来的呢?其实仿射联络「稍微组合」一下就可以和黎曼曲率R建立起关系:
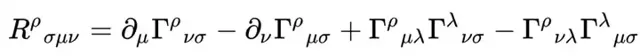
这个R是由质量生成的,它直接刻画的时空的弯曲,它「稍微组合」就可以是著名的爱因斯坦场方程
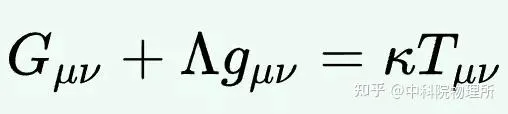
里面的那个G了。
我们可以看到,相比较于牛顿时代的 ,现代引力理论绕了好大一截。先得弄出来质量,然后得到黎曼曲率,还需要求解仿射联络,才能求出引力的效应。看起来实在是麻烦得不行,公式巨复杂,哪里有科普里说的「简单优美」啊!
但是,这恰恰就是现阶段人类所理解的引力的本质——时空的扭曲。除了爱因斯坦场方程,那些奇奇怪怪的公式,都是四维弯曲时空上几何学的结果。









