安利一本線性代數 魔法書 。
叫做【沈浸式線性代數】(Immersive Linear Algebra) 。
裏面的影像都是活的 ,能按照你喜歡的姿勢動,可以全方位觀察,有助消化艱難的理論。

這免費書在Hacker News獲得了 1200+ 的高熱,並引起了一陣「好人一生平安」的感激之情。
影像都能怎麽玩? 我們一步步看。
開啟你的魔法書
來看第三章 向量點乘 (Dot Product) 裏的一個栗子:
復習一下「投影」。你看,有一束光打在三角形上。然後,三角形背後的「桌面」,留下了它的影子。
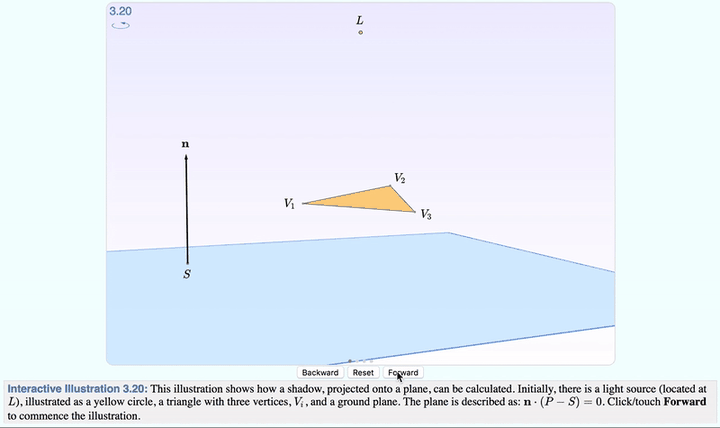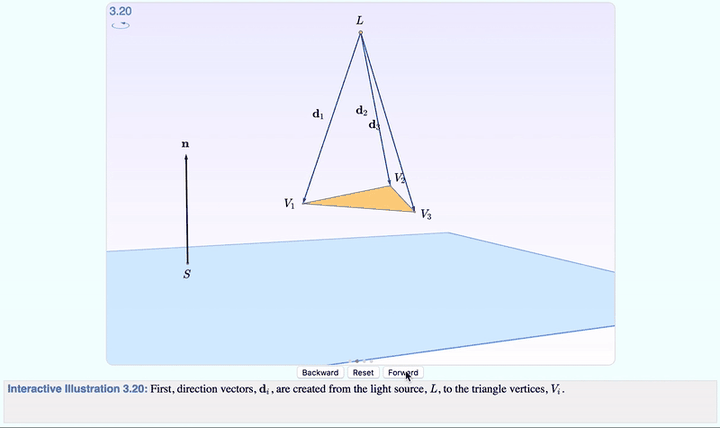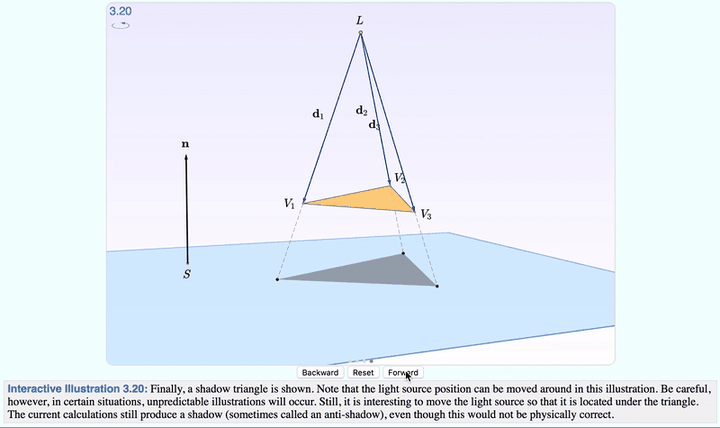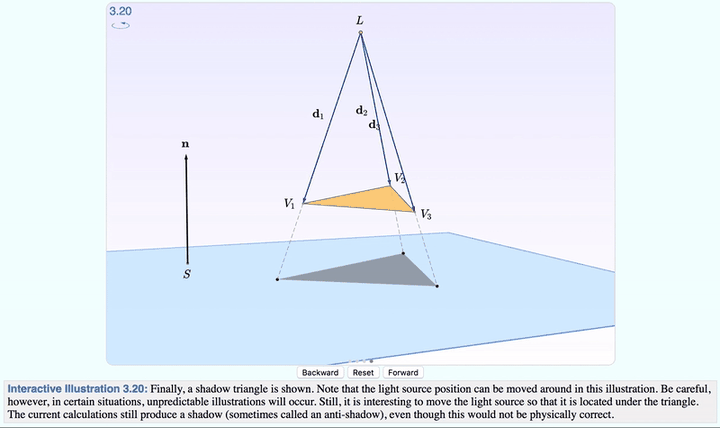
點選 Forward ,就可以分步觀察,從光線發射到生成影子的全過程了。
影像變化的時候,下面的 文字解釋 也會變,每一步要註意什麽,都寫在裏面。
如果你感覺3D影像更生動,只要點左上角的 旋轉按鈕 ,影像就會轉起來了。
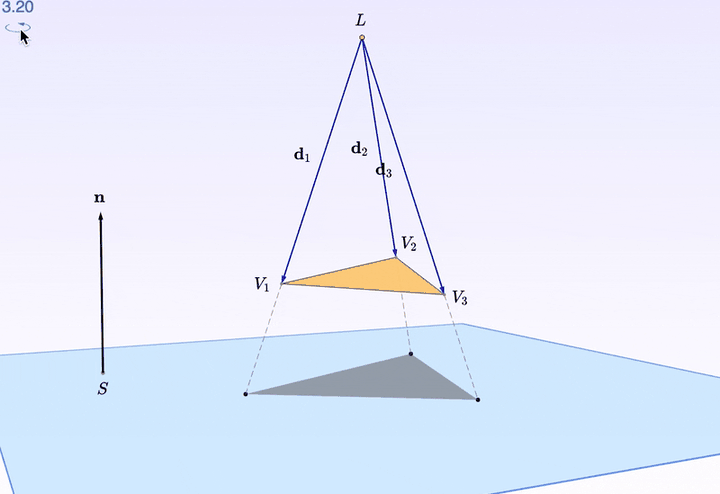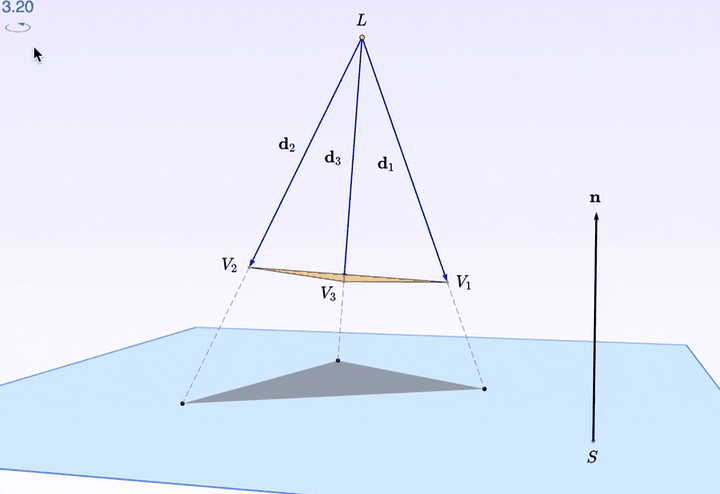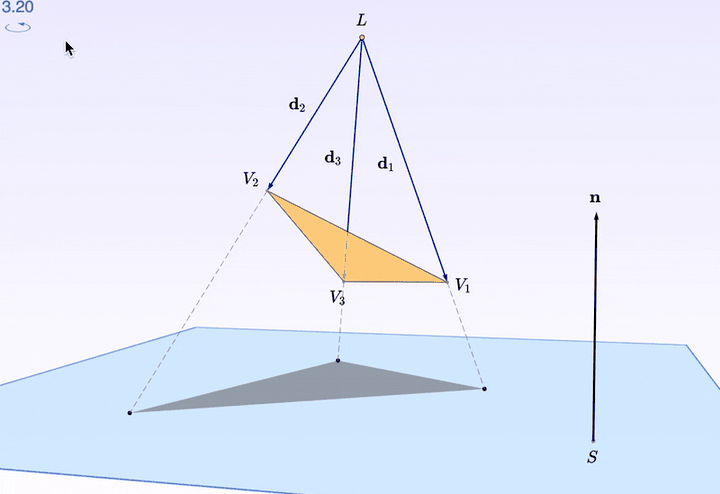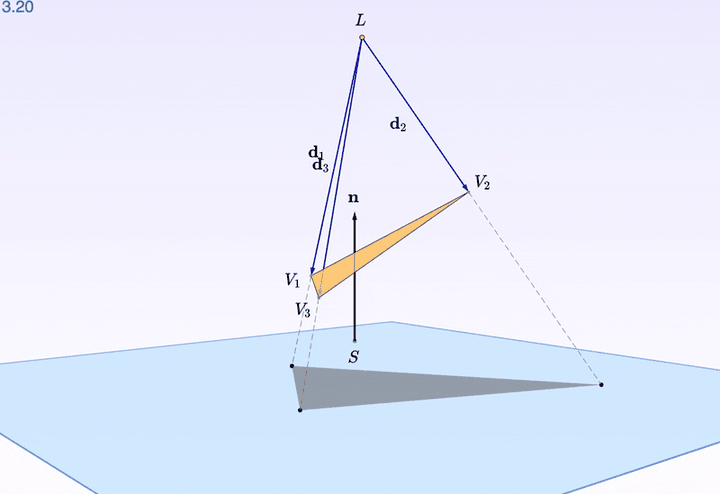
轉起來還是不夠立體?
三角形的每個 頂點 都可以拖拽。看上圖,把一個頂點往上擡了擡,是不是漂亮了一些?
除此之外, 光源 的位置也可以調。
如果,你需要某個特殊的角度觀察,比如由「桌面」出發的水平視角:
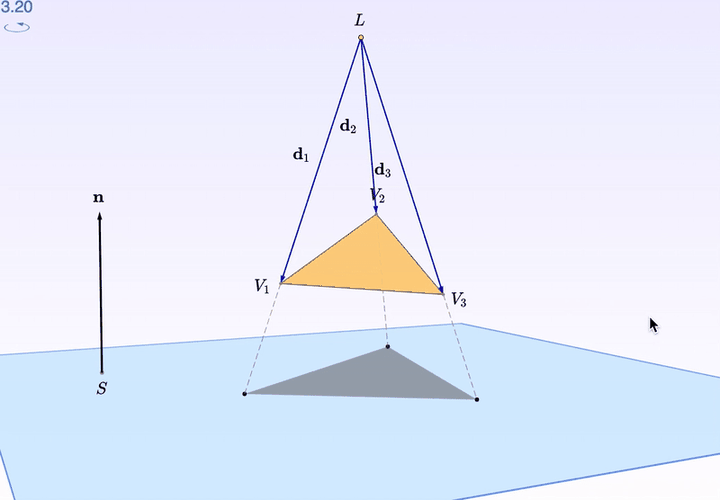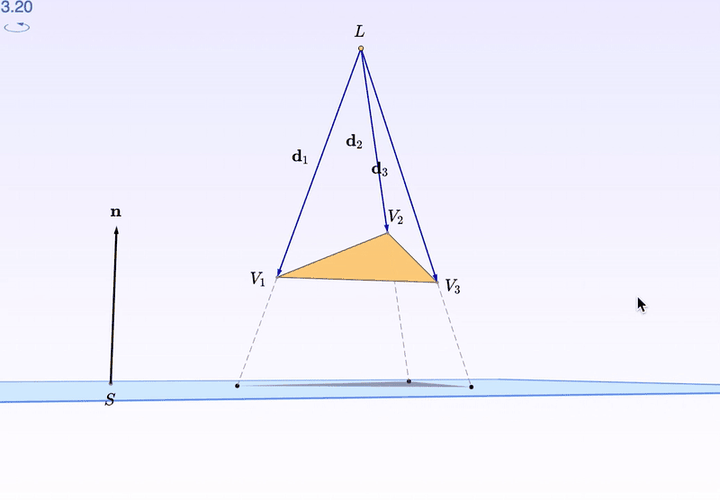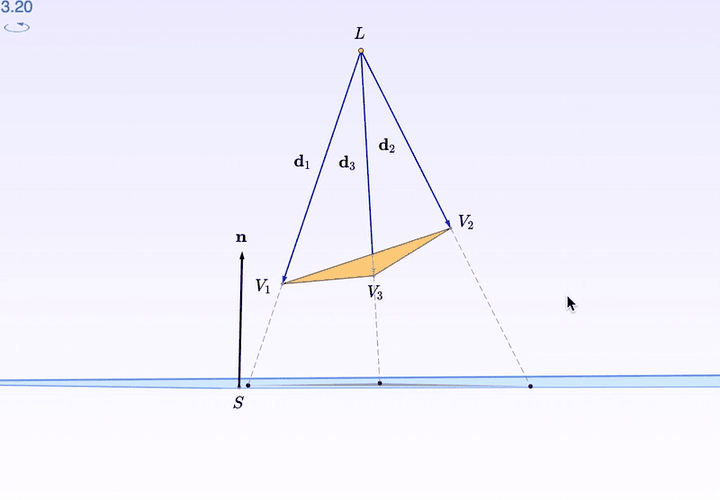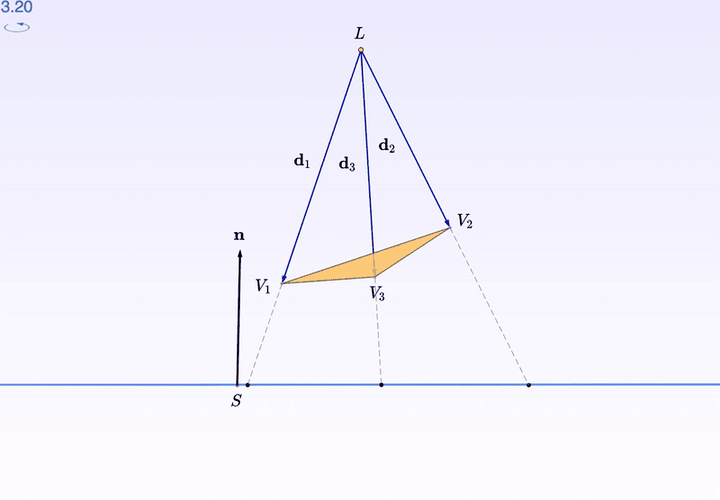
按住右鍵拖動,就可以調角度了。
調平了,再按左上角的旋轉按鈕感受一下:
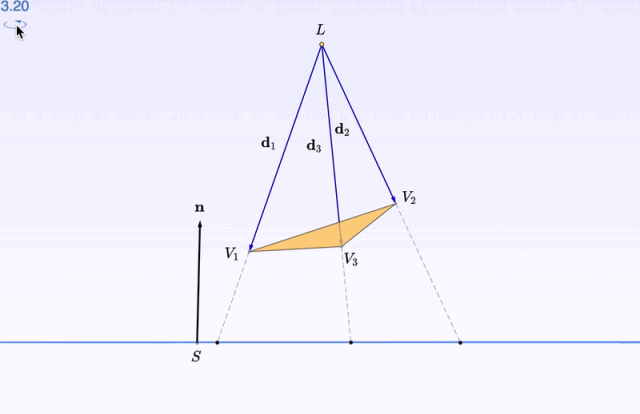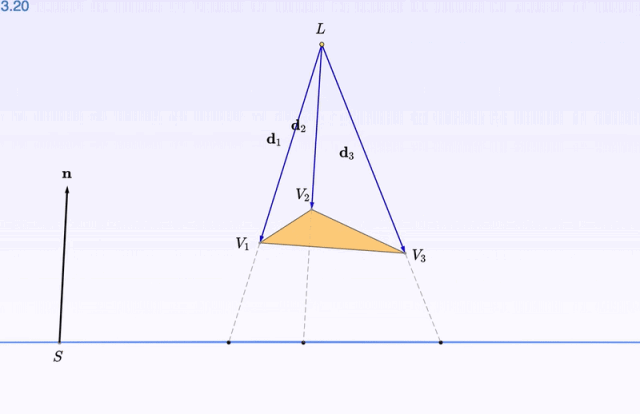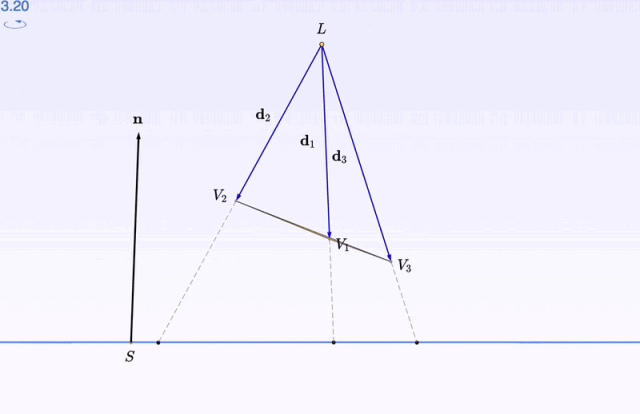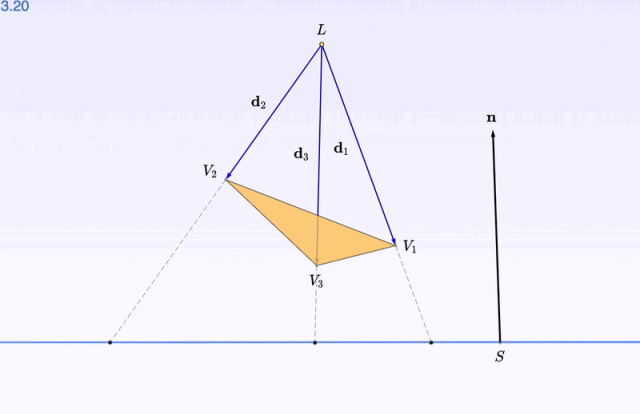
深度觀察了影像之後,再開始 數學推導 的部份:比如影子的位置怎麽算,大概就不會顯得那麽高高在上了。
另外,每當推導中用到了前面講過的 定義 ,也不用翻回去查,只要把滑鼠放在上面,定義就顯示了:

已經完全沒理由不好好學習了。
十一章
宏觀了解一下章節分布吧,你會更有食欲的。
第一章:綜述第二章:向量
第三章:點乘
第四章:叉乘
第五章:高斯消元法
第六章:矩陣
第七章:行列式
第八章:秩
第九章:線性對映
第十章:特征值和特征向量
第十一章:矩陣分解
作者團共有三人,J. Ström,K. Åström,以及T. Akenine-Möller。一人主攻數學,一人主攻圖形學,一人主攻影像編碼。
(可能是) 由於人少,從2013年寫到現在,還有兩章待續。有生之年系列。
祝福你,在第十章更新之前,學完第九章。
現在就可以開始看了:
— 完 —
量子位 · QbitAI
վ'ᴗ' ի 追蹤AI技術和產品新動態
歡迎大家關註我們,以及訂閱我們的知乎專欄











