這不是外測度的單調性,這是數學分析的極限保號性。
\bigcap_{j=1}^{\infty }E_j=(E_1\cap E_2\cap\cdots)\subseteq E_1
\bigcap_{j=2}^{\infty }E_j=(E_2\cap E_3\cap\cdots)\subseteq E_2
\bigcap_{j=3}^{\infty }E_j=(E_3\cap E_4\cap\cdots)\subseteq E_3
以此類推,那我把括弧裏面的集合用新符號來記,即 S_k=\bigcap_{j=k}^{\infty }E_j=(E_k\cap E_{k+1}\cap\cdots) ,就有 S_k\subseteq E_k ,並且每個 S_k 都可測。
於是根據測度的單調性, m(S_k)\leq m(E_k) 。
為了方便書寫,令 a_k=m(S_k),b_k=m(E_k) ,則 a_k\leq b_k 。
又因為 \left\{S_k \right\} 是遞增的可測集合列,所以 \left\{ a_k \right\} 單調遞增。
根據可測集的性質, m(\lim_{k \rightarrow \infty}{S_k})=\lim_{k \rightarrow \infty}{m(S_k)}=\lim_{k \rightarrow \infty}{a_k} 。
分類討論,如果存在某個自然數 K 使得 m(S_{K})=a_{K}=+\infty ,則等號右邊為 +\infty 。
根據 a_k\leq b_k 及數列 \left\{ a_k \right\} 的單增性,當 k>K 時, a_k=+\infty ,因此 b_k=+\infty 。從而 k>K 時 \left\{ b_k \right\} 成為常數列,因此 \lim_{k \rightarrow \infty}{b_k}=+\infty=\underline{\lim _{k\rightarrow \infty }}b_k 。
※這是數學分析中數列收斂的充要條件:
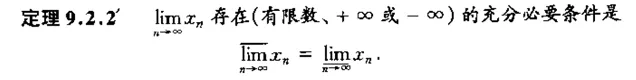
所以 \lim_{k \rightarrow \infty}{a_k}=\underline{\lim _{k\rightarrow \infty }}b_k
如果對於任意正整數 k ,都有 a_k<+\infty ,但 \left\{ a_k \right\} 是無界數列,則根據單調性, \left\{ a_k \right\} 發散至 +\infty 。從而根據 a_k\leq b_k 可知 \left\{ b_k \right\} 也發散至 +\infty ,這種情況和上一種相同。
如果對於任意正整數 k ,都有 a_k<+\infty ,但 \left\{ a_k \right\} 是有界數列,則根據單調有界定理, \left\{ a_k \right\} 收斂。
根據定理:
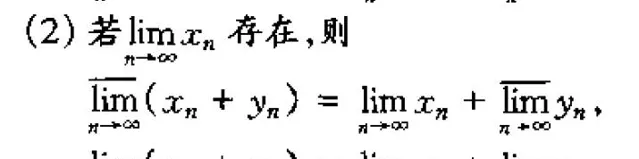
取 x_n=a_n,y_n=b_n-a_n\geq0 ,就有 \underline{\lim _{k\rightarrow \infty }}b_k=\lim_{k \rightarrow \infty}{a_k}+\underline{\lim _{k\rightarrow \infty }}y_k 。
但 y_k\geq0 ,它的每個子列也都非負,從而每個子列的極限非負。根據下極限的定義, \underline{\lim _{k\rightarrow \infty }}y_k\geq0 。這樣就有 \underline{\lim _{k\rightarrow \infty }}b_k\geq\lim_{k \rightarrow \infty}{a_k} 。
綜上, \lim_{k \rightarrow \infty}{a_k}\leq\underline{\lim _{k\rightarrow \infty }}b_k 成立。











