設剩余次數 n 時, 預期的點數期望為 \mathtt{dp}[n] .
只要本次點數比剩余期望大就行.
\mathtt{dp}[n]=\frac16 \sum_{i=1}^6\max(i, \mathtt{dp}[n-1])
沒次數時, \mathtt{dp}[0]=0 , 等死, 大於0就要, 總不能不要吧...
dp
[
0
]
=
0
;
dp
[
n_
]
:=
dp
[
n
]
=
Sum
[
Max
[
i
,
dp
[
n
-
1
]],
{
i
,
1
,
6
}]
/
6
;
chance
=
Reverse
@
Table
[{
i
,
N
[
dp
[
i
],
3
]},
{
i
,
0
,
#
}]
&
;
chance
[
12
]
//
TableForm

- 1-4 次拋之前遇到 6 就收手
- 5-7 次, 大於 5 收手
- 第八次大於 4 就要收手了
不過...多半是收不了手的...
P=\left(\frac{5}{6}\right)^4 \left(\frac{4}{6}\right)^3 \left(\frac{3}{6}\right)^1=\frac{625}{8748}\approx 7.1\%
隨著機會減少, 做人底線逐步降低.jpg
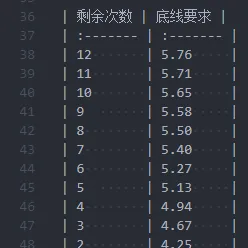
當然, 我們甚至可以很無聊的把這個數列解出來:
\begin{aligned} G_6(x) &= -\frac{2 x^5+10 x^4+15 x^3+45 x^2+468 x-756}{180 x^2-396 x+216}x\\ \mathtt{dp}[n]&=g_6(n) =\begin{cases} 7/2 & n=1 \\ 17/4 & n=2 \\ 14/3 & n=3 \\ 89/18 & n=4 \\ 6-47\cdot 2^{4-n} 3^{2-n} 5^{n-5} & n>4 \\ \end{cases} \end{aligned}
可以看出次數增長時, 期di望xian以指數趨向於 6.
啊, 這不是廢話.....











