首先,關於時間箭頭,涉及到科學和哲學的廣泛討論,包括諸如 因果箭頭、心理學箭頭、熱力學箭頭、電動力學箭頭、宇宙學箭頭、量子力學箭頭 等等。本文盡量弱化哲學討論,盡可能地聚焦在科學角度。主要談論一下熱力學和量子力學箭頭。(已有答主從時空結構的角度談論過這個問題了,這裏我不再狗尾續貂)
0,在談論之前我先澄清一件事。
當我們說「時間箭頭是單向的」或者「流動是單向的」,我們說的是什麽東西?
從表面的語意上來看,我們假定存在著一種東西,叫做「時間」。這種東西是在流動的 - 它的流動方向不受任何事物的影響,總是「朝前」的。
但是,從物理學的角度,更加自然的做法不是去討論「時間本身」的「流動」,而是把時間作為一個事件有序排列的維度。所謂的「時間箭頭」,不是時間本身是不是有一個箭頭,而是討論 在時間維度上,物理現象的不對稱性 。也就是說,在時間序列中,它的兩端有著顯著差異,於是我們就有了「歷史」和「未來」的區別。是事件序列的不對稱性賦予了「時間」一個箭頭。
我可以姑且把前者叫做「時間流動」圖景,後者叫做「時間序列」圖景。
至於為何我們不采取第一種 把時間看做是一種流動的實體 的看法,我們後面再說。
另外,關於時間箭頭的科普可謂是汗牛充棟。但是真正說得特別清楚明白的,卻不多見,往往失於偏頗,或者根本就不能解決問題。這裏我向大家推薦一本科普著作:
Sean Caroll寫的 From Eternity to Here: The Quest for the Ultimate Theory of Time . [1]
語言簡單,並且論述相當清楚。亞馬遜的audible還有他自己朗讀的有聲書,不得不說,他的聲音也挺好聽,並且讀得十分清晰,聽力不好的人都可以聽明白,開車的時候聽一聽,非常有舒緩心情之功效。
1,首先說一下熱力學箭頭。
所謂熱力學箭頭,指的就是熱力學第二定律的結論:孤立系統的熵總是增加。如果我們把整個宇宙看做是一個孤立系統,那麽宇宙的熵就是不斷增加的。那麽,在整個宇宙的歷史線上,就必然 兩端不對稱 :一端低熵,我們稱之為「歷史」,另一端高熵,我們稱之為「未來」。於是,熵就成了一種時間箭頭。
我的歷史回答中,曾經詳細談論過一個問題,就是為何微觀定律時間可逆,熱力學上卻總是熵增?諸如這兩個答案:
這裏的核心問題就是,從底層的動力學方程式中,我們看不到時間的兩個方向上有所區別(也就是說,我們把方程式做一個時間反演操作,所有的物理學定律仍然成立)。無論是經典力學還是量子力學,都沒有對「時間方向」有所限制。但是為何建立在這些方程式基礎之上的熵增定律卻明確地規定了世界必須從低熵向高熵演化?
統計力學對此的回答,現在尚有爭論。但是現有的比較公認的有兩件事,簡言之:
- 相空間的結構是不對稱的
- 初始條件問題
用「人話」來講,就是
- 高熵是極大可能出現的狀態,低熵是基本上不可能出現的狀態
- 我們現在的宇宙狀態就是極不可能出現的低熵態
下面我一一道來。
1.1,相空間的不對稱性
在講這個之前,我要說明一下,下面這一小節基本上都是從經典物理圖景出發來闡述的。這是因為,從經典向量子的推廣,並沒有什麽原則上的限制。並且關於量子的討論我們可以展開一點點,放在後面。
好了,現在我們來說一下,什麽是相空間呢?
理論上,我們可以把構成宇宙的所有粒子的狀態(經典物理上,就是每一個粒子的動量和位置,量子物理上,就是態向量)描述出來,這樣一來,我們就把宇宙的狀態描述出來了。
我們可以想象,我們能把宇宙的所有可能狀態組成一個集合。這個集合用下面一個圓圈表示
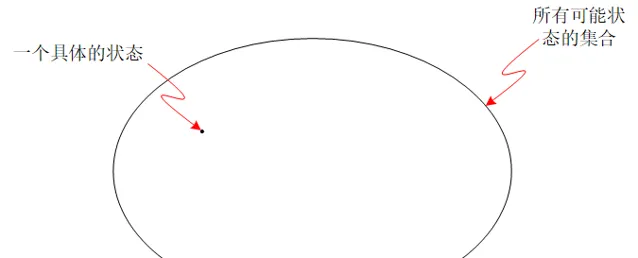
那麽,這個「圓圈」所圈定的空間,就叫做「相空間」,這個空間中的每一個點,都是一個宇宙的可能狀態。
這種狀態,是從微觀層面上對宇宙做出的完整描述 - 我們對 每個粒子 的狀態都做成精確的描述。宇宙的狀態,就是所有粒子狀態的集合。每個粒子有三個維度的位置自由度和三個維度的動量自由度。那麽宇宙的狀態就由6N個變量描述出來(N是宇宙的粒子數目)。這種狀態,叫做 「微觀態」 。
但是實際中我們對一個系統的描述不可能做到微觀層面。這需要太多的數據了。可以粗略估算,1mol的理想氣體,如果我們用單精度浮點數來描述這些變量(事實上這是一個相當粗糙的精度!),大約需要1YB的儲存空間,是現在全球總儲存量的3萬多倍!
現實中可行的辦法就是忽略具體粒子,只從宏觀上對整體狀態做出描述。例如說,對理想氣體我們不去管裏面的每一個分子是怎麽運動的,而是只考慮宏觀上它的一些統計平均的東西,諸如溫度、壓力、密度等等。也就是說,我們僅用不到1KB的數據來粗略描述1YB的資訊。
這個,叫做「 宏觀態 」。
於是,我們就會發現,大量不同的微觀態,在宏觀上我們是分不出任何區別的。舉一個形象點的例子,星爺的滿頭灰發:

從微觀上來講,我們把他的一根黑發和一根白發互換一下位置,這肯定是兩種不同的「發型」。但是從宏觀上,我們沒有辦法區分。當我們說宏觀上的「灰發」的時候,我們可能在談論無數種「微觀發型」。我們從宏觀上,可能只需要一個變量,「灰度」,就概括了這無數種情況。
一個非常直觀,但在統計力學裏面極其重要的事實就是, 有些宏觀態對應著大量的微觀態,而另外一些宏觀態,對應著極少量的微觀態。
我們還用星爺的頭發來說這件事。均勻分布的黑白發,就對應了很多種不同的微觀分布:我們可以想想,隨便互換一根黑發和一根白發,都不影響「均勻分布」這種情況。但是,如果是這樣一種分布:

就完全不同了。這種發型只有一種微觀的分布。隨便互換一根黑發和一根白發,都會破壞「半邊黑半邊白」這種發型。
如果黑白發的數量各占一半,它們隨機分布的話,顯然極大可能出現星爺的灰發,極不可能出現半邊黑半邊白的頭發。前者是極大概率事件,後者是幾乎不可能出現的事件。
就像科普書裏說的,把黑砂和白砂混合在一起,搖晃兩下,我們會發現黑白混合均勻,有可能會出現黑砂全部跑到左邊,白砂全部跑到右邊的情況嗎?有,但是幾乎不可能。原因是,均勻混合有無數種混合方式,半黑半白則只有一種。前者是極大概率事件,後者是極小概率事件。
基於這個基本的道理,我們用下面這個著名的公式來定義熵(這大概是一根學者所能想到的最浪漫的墓誌銘了)。
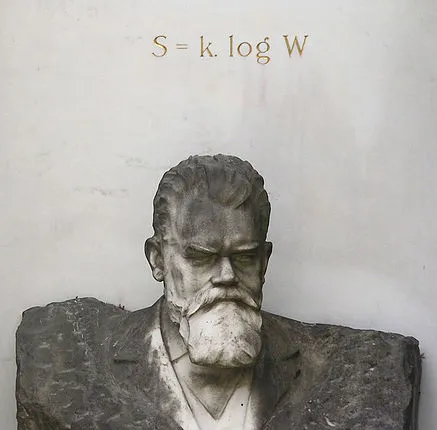
在這個公式裏面, S指的是一個宏觀態的熵。W指的是這個宏觀態包含的微觀態的個數 。對一個宏觀態而言,它包含了若幹種宏觀不可辨的微觀態。這些不可辨微觀態的個數越多,這個宏觀態的熵就越大。相應地,如果每種微觀態都是隨機出現的,那麽 熵更大的宏觀態出現的概率就越高 。
如果我們數一下一個宏觀態中包含的微觀態的個數,這不可避免地要用到排列組合的計算。大家知道,排列組合的一個顯著特征就是,它的數目是由其中粒子個數的階乘決定的。也就是說,當粒子數足夠多的時候,W將會是一個天文數碼 —— 相應地,這裏談論的「更高概率」和「更低概率」的差距也就是天文數碼。一個高熵態出現的概率相比低熵態出現概率,何止億萬倍。
也就是說,對於宏觀系統(>10^23個粒子), 存在著一種宏觀態,其出現的概率遠高於其他狀態出現的概率 。因為該宏觀態所包含的微觀態數目遠高於其它宏觀態所包含的微觀態數目。
這個宏觀態,就是 平衡態 。也就是熵最大的狀態。
我們來舉一個簡單的粒子。有一箱的理想氣體,現在我們把箱子分成相等的左右兩部份,那麽兩部份中的分子數各自是多少呢?如上所述,我們有兩種方法來回答這個問題,第一種,就是跟蹤每一個分子,諸如「分子1號在左邊,2號在右邊,……」,這就是微觀態;第二中,我們整體描述,「大約有多少比例的分子在左邊,多少比例的分鐘在右邊」,這就是宏觀態。
現在我們考慮所有的可能,可以是所有的分子全部在左邊,也可以全部在右邊,也可以一半一半。總而言之,一共有 2^{10^{23}} 種可能的狀態。那麽,我們考慮兩種極端情況:
1、所有的分子全部在左側,只有一種分布狀態是這種情況。
2、一半在左側,另一半在右側。我們可以透過Stirling公式估算出這種分布的可能數目,大約是 \frac{2^{10^{23}}}{10^{11}}\simeq 2^{10^{23}} 種這樣的狀態。
請停下來,仔細考慮一下第二種情況下的那個數碼是什麽含義。可以說,它和無窮大的區別僅僅在於,我們還可以用一個數量級來描述它。也就是說,它practically和無窮大沒有什麽區別。那麽,相比於第二種情況(完全均勻的分布),第一種情況(完全不均勻分布)幾乎不可能出現。
那麽,我們回到前面的相空間話題。相空間包含了所有可能的微觀態。從上面這個論述中可以看出,在這個空間中,絕大多數的微觀狀態對應著平衡態。也就是說,基本上整個相空間都被那些高熵態填滿了。低熵態幾乎不占體積。形象地比喻一下, 低熵態的體積就是在整個宇宙中的一粒塵埃 - 這個比喻只是形象,並不準確。事實上,低熵態的體積比「塵埃」還要小的多的多。
或許我們可以借用潘洛斯的插圖來表示這種情況 [2] :
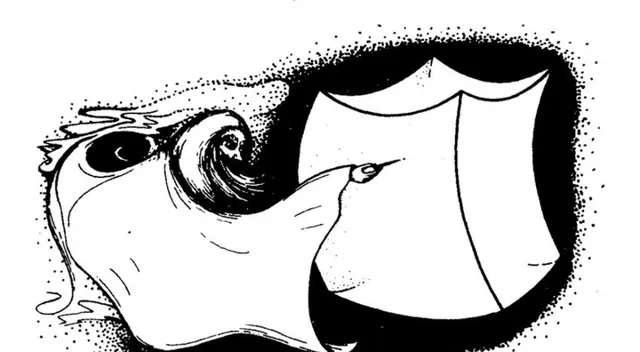
這張圖說的是,只有上帝才能用它那極細小的針頭點到那個幾乎不可能出現的那個狀態。
宇宙的演化,就是宇宙狀態隨著時間的變化。用我們前面那張形象的圈圖表示,它的整個歷史線就在相空間中劃出一條 軌跡(動力學中把它叫做trojectory) 。
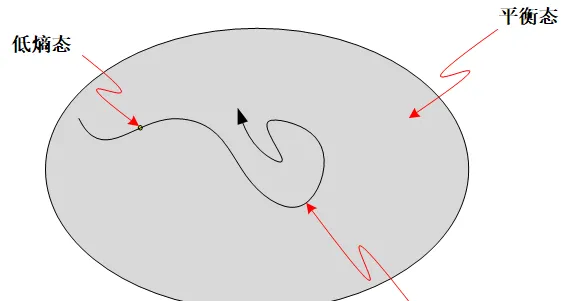
那麽我們現在可以來看時間箭頭的問題了,我們來打一個比方,比如說你現在處在一個黑暗的外太空,沒有任何條件限制你往哪邊走。你可以往前,也有同樣的自由往後。你可以說你的運動是對稱的。
整個空間只有你的身邊有一盞燈並且這是宇宙中唯一的一盞燈,燈很小,發出一點點微光。

現在你開始向著某個方向走。
這時候我來問你,你對你的未來的亮度有何預測?
這是個簡單到令人發指的問題,你用頭頂的那一根珍貴無比的頭發絲想一下都知道答案:你的未來亮度一定是變暗的。雖然沒有人限制你往哪個方向走,但是問題是基本上所有的方向都是變暗的。
這盞小燈,就類比了相空間中的低熵區。我們由此可知,這個粒子無論如何,最終幾乎必然向高熵演化 —— 歷史與未來是不對稱的。原因是,相空間中高熵區和低熵區是不對稱的。這和粒子自身的運動方程式是不是對稱的沒有關系。
說到這裏,似乎都很完美。但是,故事並沒有結束。
1.2,初始條件問題
從前面的討論,我們可以得到一個結論,高熵是極高概率的,低熵是極低概率的。但是如果我們仔細分析這個結論, 我們能得到時間箭頭的合理解釋嗎?
答案是不能。
因為從上面的論述中,我們只能得到這樣一個結論,「 如果我們現在處於低熵區 , 那麽後續 我們幾乎必然向著高熵區演化」。請註意黑體的部份,我們從熵的統計解釋到時間箭頭之間,多了一個前提條件:「如果我們現在處於低熵區,那麽後續……」。
而這個多出來的前提,則是一個麻煩制造者。
首先,既然前面分析了,低熵區是一個極端不可能的狀態,那麽按理說我們就極端不可能處在現在這種狀態。在相空間中幾乎所有的演化規矩 —— 也即是最可能發生的演化 —— 是從高熵區向著高熵區演化 —— 也就是說,熵不變。
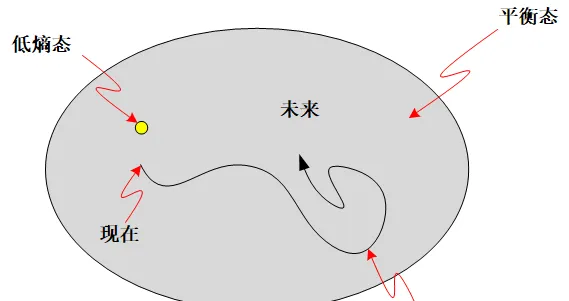
而我們現在談論的,卻是一種極端的情況,我們把演化的出發點限制在一個非常極端的位置(請註意下圖中低熵區的畫法是極度誇張的,它根本就沒有那麽大):
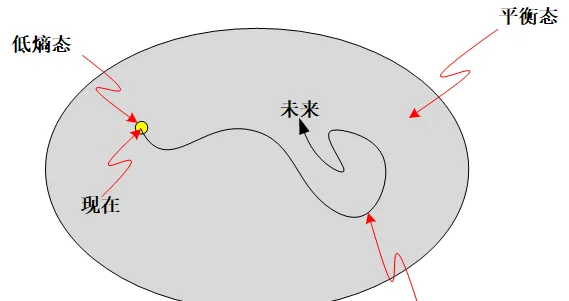
好吧,你可以說,即使是極端不可能出現,可是我們的的確確恰好處在一個極端狀態啊。這是一個簡單事實。
所以,我們等於在說,「由於我們現在處於低熵態,所以未來更可能向著高熵態演化」。這個從邏輯上很簡單。但是對時間箭頭這個問題來說,就比較尷尬。我們現在預設了時間序列的一端是低熵,那麽另一端是高熵就不言而喻了 —— 高和低總是相對的嘛。
這個回答其實就是預設了時間箭頭的存在,來解釋時間箭頭。因為我們假定的前提就是,我們的起點是一個特殊的點。也就是說,我們指定了「現在」的特殊,以及未來高概率的「普遍」,來解釋現在和未來的不對稱。
為了把這個矛盾放大,我們可以用同樣的邏輯來回溯歷史:「假設我們現在是低熵,那麽歷史上宇宙從何而來?」
因為宇宙極大概率是高熵的,所以這個問題的答案就是,極大概率上,歷史也是從高熵而來。也就是說,歷史上極大概率是熵減 —— 即歷史上「 時間箭頭是反向的 」。
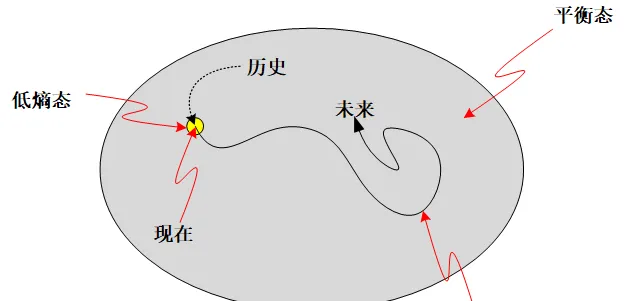
如果我們要保證我們的時間箭頭總是「朝前」,我們就需要假定歷史上它是從更低熵演化而來。那麽歷史的歷史上它就從更更低熵而來……,然而熵是有下限的——也就是零。我們這麽追問下去, 就追到宇宙的起點了: 宇宙必然是從一個極其低熵、極端不可能的情況出現。
為了使我們的時間箭頭有意義,我們得到了「宇宙起源於一個極端情況」這種結論。 這幾乎就是赤裸裸地先打靶後立靶 (beg the question) —— 如果我們不能從其它的地方來justify「宇宙起源」這個問題的話。
這就是 宇宙學箭頭 。但是這裏我不打算就此展開,因為首先它還有很多爭論,其次我也不是宇宙學的專家,說出來的話幾乎必然是錯誤的。
我們可以弱化我們的討論,不論如何,現在的一個簡單事實就是,我們是一個低熵宇宙,所以未來它向著高熵宇宙演化就是自然而然的結論,所以現在我們感受到了時間箭頭。
這就是初始條件問題。
總而言之,前面兩個問題,一個指出,「存在著一些極端的情況」,另一個指出「我們現在就是一種極端情況」。兩者結合,才能得到時間箭頭的解釋:未來高概率是一種普遍情況,當然和現在我們的極端情況不是對稱的。
時間不對稱,是因為我們本身就問了一個不對稱的問題。
2、「無知」的野蠻生長。
前面說的是一種大家最常用的熵的統計詮釋,波茲曼熵。
但是,統計力學的基礎問題其混亂程度,遠遠高過其它物理學分支,量子力學雖然爭論良多,但是至少還有一套統一的「正統」形式理論。統計力學其眾說紛紜的程度則更甚。這裏我們還可以從其它角度來闡述熱力學箭頭。
比如說吉布士熵。 如果說波茲曼熵說的是狀態的體積,吉布士熵說的就是狀態的密度 - 它的概率密度。如果說我們談論平衡態,對應著同樣的宏觀性質,這兩者是有一一對應關系的:的確,密度越高,則體積越小嘛。也就是說,在這種情形下,它們是等價的。
但是在多數情況下, 吉布士熵和波茲曼熵其實是不等價的 。吉布士熵和波茲曼熵的區別就在於,在波茲曼熵中,我們對一個 確定的宏觀狀態 下,來計算所有能夠表現為這種宏觀態的微觀狀態的數量。但是對吉布士熵而言,我們對微觀態的計數範圍,是從某個 特定初始條件 (範圍)出發、演化所能到達的所有可能狀態。兩者的計數範圍都不同,當然計數的結果就不同。嚴格講,它的計數範圍要比波茲曼熵小得多:因為它受到初始條件的限定。
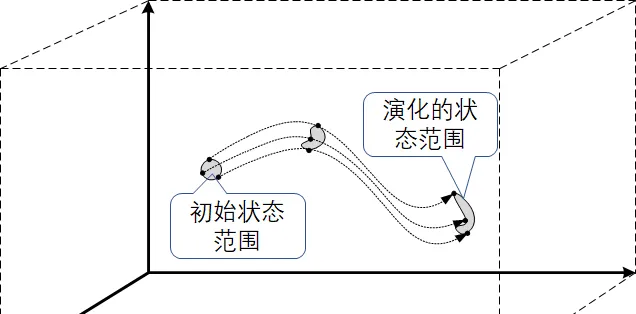
這會給吉布士熵帶來很多優點,例如說它不要求等概率、不要求平衡態等等。但是,如果我們計算吉布士熵的演化,我們會發現它是 守恒 的。也就是說,根本就不存在熵增!所以,嚴格講,吉布士熵其實是時間對稱的。這其實很容易理解,因為它的演化是從嚴格的微觀動力學推演的。 微觀動力學的對稱性就決定了吉布士熵的對稱性 。
那麽,吉布士熵的統計力學描述,豈不是和熱力學熵不一致了嗎?它並不能給出熵增的結果啊。
答案在於「 粗粒化 」。我們對任何系統的任何觀察,都不可能是100%精確的,我們觀察的結果,都是一個大致範圍。比如說一個人身高175.5cm,其實一般的測量精度給出的,大約是在175~176之間的範圍。也就是說,我們日常經驗到的世界,都是粗粒化的。
比如說,我們對系統的初始狀態指定一個概率分布(一個初始粗粒)。這個分布的體積越小,就越精確,也就意味著我們對它的認知就越確定。
但是,隨著系統的演化,這個概率分布就會發生各種形變。由於運動方程式本身的時間可逆性,這個分布的 體積不會發生變化(也就是熵守恒) 。但是它的形狀卻會越來越復雜。運動方程式的非線性就決定了,它會演化成一種 碎形結構 。下圖形象化地描述了碎形的特征。一個很小的初始粗粒可以被拉長成任意長的纖維(理論上的確可以是 任意 長的),然後編織起來團成一個線球塞滿整個相空間。在一個可以 無限精度觀察 (細粒化)的觀察者看來,無論它是如荷西滿相空間的,它的體積不變:也就是概率分布是不變的,即熵守恒。線球再大,其內部基本上都是空隙。但是對一個粗粒化的觀察者看來,當這個線球精細到一定程度,我們就只能看到一只球,我們無法分辨任意細的纖維。我們隊它的精細結構的知識就遺失了,因而它的體積似乎是擴大了。

也就是說,當我們不去精確追蹤系統的演化,而是為演化設定一定的精度(相空間粗粒化),我們會發現我們對系統越來越無知,我們對系統的確定性越來越喪失了。
那麽,隨著系統的演化,我們對系統的知識不斷地遺失(因為相空間結構的精細化)。這就是熵增。從這個角度上看,熵並不是我們科普語言中的「 混亂度 」而是我們的「 無知度 」。這就是1970年代發展成熟的熵的主觀詮釋(主要來自Jaynes的工作) [3] 。簡言之:
因為我們無法精確跟蹤系統的演化(基於系統演化的混沌特征),所以我們對系統的無知程度不斷增加,這就是熵增。
統計力學本身就是粗粒化的學問。 如果我們能精細了解系統的運動,就沒有任何統計力學的生存空間。
那麽當我們談論一個系統的熵的時候,首先要問的問題是,你用何種精度的自由度來定義成你的熱力學系統?你的知識,決定了熵的大小。故而, 熵就是你對系統的無知程度, 也就是你對系統資訊的掌握程度。如果我們做不到無限精度,只要對系統有一點點的無知,這種無知就會隨著時間迅速地野蠻生長(事實上,是指數速度生長)。於是很快地,我們就遺失了我們對系統的所有細節知識,只留下了了幾個宏觀量的認知 —— 這就是平衡態。
於是,我們把我們能相對確切認知的那一端,叫做歷史,把我們無法確切認知的那一端,叫做未來。這就是一種非常符合直覺的時間箭頭了。
關於相空間、演化、混沌、碎形等的進一步討論,請參考本人專欄:
3、一點點量子調味品
當我們開始考慮量子力學的時候,一定要小心翼翼。量子力學和經典力學有著非常本質的區別,很多時候我們容易把它們混淆起來。例如說,用量子不確定性來解釋熵,這中間陷阱重重。很多哪怕是專業人士,都容易落入其中
我們來考慮前面提到的「線團」的類比。這是一種碎形結構,它的特征就是無限精細。但是,還有一個關鍵因素,就是它的形成依賴於非線性演化。不僅如此,混沌系統的最基本特征,對初始條件的極端敏感(SDIC)也依賴於非線性演化。
然而量子力學是線性的。
如果我們用不確定原理來討論問題,就意味著我們用量子力學來處理問題了。那麽我們就要改用薛定諤方程式而不是哈密頓方程式。那麽混沌就失去存在基礎了,因而就沒有前面所說的那種精細結構,因而不確定原理也就不能成為粗粒化的理由。這就是為何Robert Bishop說:
Quantum chaos, or quantum chaology as it is better called, is the study of the relationship between chaos in the macroscopic or classical domain and the quantum domain. [4]也就是說,大家對量子混沌的研究,其動機並非因為量子中存在混沌現象,而是要尋找經典混沌的量子起源:為何一個不能容許混沌現象的底層理論在宏觀上產生了混沌現象?其根本就是 量子-經典過渡問題。
所以說,在量子領域中,真正的問題就是這個量子-經典過渡問題,也就是所謂的「波函數塌縮」問題。用不確定原理在經典混沌理論中的解釋是無效的。
談論量子理論,我們應該首先明確一點, 量子力學和經典力學一樣,也是時間對稱的。
在「 正統」詮釋裏面 ,這似乎不對。「波函數塌縮」似乎不是時間對稱的。對一個已知量子態,我們的觀測結果就是某一個本征態,它出現的概率就是由波恩規則決定的、不可預測的。按照前面「熵即無知」的解釋,我們在沒有看到結果之前對它確實是無知的。難道觀察行為不會造成熵增嗎?
這個問題就比較微妙了。
如果我們用馮諾依曼熵來做一個計算,我們的確會得到這樣的結果:對一個純態進行觀察的前後,熵是增加的(對一個混合態的觀察會復雜一些,這裏就略過)。也就是說, 波函數塌縮看似的確引發了馮諾依曼熵的熵增 (我們這裏暫時不去討論「塌縮」這個概念本身是否有效)。那麽這是否就是熱力學熵增的起源呢?
對此我們還是懷有疑慮的。量子熵增和經典的熵增很不一樣。在經典力學裏面,我們的無知指的是「系統的狀態在那兒,我們不知道確切的狀態為何」,而在量子系統中,則是「我們知道系統的量子態,對一個觀察結果我們不知道」。
也就是說,在量子力學裏面我們通常討論的觀察問題,其實也是在問一個不對稱的問題:
「已知量子態,我們會得到何種觀察結果,它又會塌縮到哪一個本征態?」。
這裏我們假定了一個 初始的純態 作為前提,也就是限定了初始態為確定的量子態。
和前面類似地,我們不妨反過來問:
「現在我們透過觀察得到了一個確定的觀察結果,那麽歷史上它從何演化而來?」
我們知道量子力學的常規套用是已知歷史知識,我們用它來預測未來。那麽這個問題則是,已知未來,我們如何用它來反推歷史?這個問題並不難,透過概率論的基本原理和薛定諤方程式,我們的確可以反推歷史。結果很有意思,也就是說,我們對歷史的反推得到的和對未來的預測結果完全相同!也就是說,從這個角度上說,即使是塌縮過程,也是時間對稱的。這個就成為所謂的「 Two state vector formalism」(TSVF,雙態表述) 的來源 [5] 。在這個理論中,向前的演化和向後的反向演化共同構成了一個系統量子演化的全部資訊,它是完全時間對稱的。
更加重要的是,關於「塌縮」,現在越來越多的人相信,它只是一個方便的工具,而不是真實存在的物理過程。這就是以多世界理論為代表的所謂的「純么正量子力學」的主張。如果沒有了塌縮,量子力學就是一個純么正的演化,當然是完全時間對稱的。對一個純態而言,無論如何,它的馮諾依曼熵總是保持為零。
那麽,熵增是如何來的呢?
這就需要我們掰開了揉碎了把「塌縮」這個概念搞清楚。這裏空間太小我寫不下,但是還是可以大略描述一下。
觀察意味著纏結,纏結意味著不可分割 。而不可分割就意味著「整體>所有部份的加和」。這就是著名的subadditivity:
S_{AB}\leq S_A+S_B
也就是說,當我們用一個儀器完成了對系統的觀察時,我們並沒有「塌縮」掉系統的量子態。我們只是使儀器和系統互相纏結起來了而已。此時,如果我們分析(系統+儀器)這個復合系統,我們必然會得到熵仍然為零的結論。但是,如果我們單獨觀察系統和儀器,然後把它們加起來,我們就會得到熵增的結論(也就是「塌縮」的結論)。 那部份額外的熵從哪裏來?就是從我們忽略掉的儀器和系統之間的纏結資訊而來。
事實上,從去相干的角度,所有這些都是可逆的,理論我們完全可以逆轉一個「塌縮」,從而回到初始狀態。但是實際上這是不可能的。 因為系統無時無刻不在和環境發生纏結,和整個宇宙發生纏結,乃至於這些纏結資訊擴散到整個宇宙當中。而我們無法對整個宇宙完成觀察!這就解釋了為何我們對系統的知識總是在減少 - 也就是說熵總是在增加。
而「和整個宇宙發生纏結」意味著什麽?意味著多世界理論中的「世界分支」。也就是說,在多世界理論中,熵增總是可以跟越來越多的世界分支聯系在一起。
這一切看起來很美好,然而,其實這只是我暫時的一廂情願。因為科學家們並沒有就「塌縮」這個問題達成共識。
4、假如「時間倒流」
我以前回答過一個問題,
我的答案是:一個熵減的世界大概和我們現在的世界沒有什麽不同。
這個回答可能和絕大多數人直覺中的答案完全相反。畢竟,物理學最基本的定律之一,熱力學第二定律,如果是完全逆轉的,怎麽可能整個世界還會是一樣的呢?
因為不論是熵增還是熵減,都是時間序列的不對稱。只是「未來」和「歷史」調換了一下而已。
而底層的物理定律畢竟是可逆的。
那麽這時候,我們可以來想象一個熵減的世界了。我們只需要把所謂的初始條件問題改為末態條件問題就好了。解過微分方程式的人都知道,這兩者在數學上毫無分別。就好像我們對自由落體過程的時間序列兩端做出不同的定義,並不會改變它的物理合理性一樣(因為自由落體和豎直上拋都是物理上合法的運動),無論是初始條件還是末態條件對我們而言,其實物理合理性不會有什麽不同,甚至我們可能壓根兒就無法覺察我們的世界現在是「熵減」的 —— 因為我們會習慣性地把熵減世界中的未來當成「歷史」。
這裏我們回到了文章最開始的聲明:我這裏談論的所謂時間流動,並不是一個真正存在的正在流動的東西,而是時間維度上物理現象的不對稱性。
從物理主義的角度,一個脫離於物理過程的時間箭頭是沒有意義的。 我們所體驗的,不是時間本身的箭頭,而是物理過程在時間維度上的不對稱性 :時間,就是微分方程式中的那個與實數軸同構的「t」。這個「t」向著兩端任意延展,但是這兩端的物理圖景有著不同的結構。一端,是確定的,「低熵的」;另一端,是不確定的,「高熵的」。 我們是用熵增的方向來定義了時間的方向,而不是沿著一個預設的時間方向發現了熵增。 從這個意義上講,考慮「熵減」並不是物理的,而是語意學的。熱力學第二定律說的,其實也不是熵增,而是熵在時間軸上的不對稱。
我們不妨這樣想象我們的一生。如果我們把時間反演,我們將會從骨灰盒裏爬出來,變成老人,越來越年輕,最終變成小孩,再爬回娘胎,變成受精卵,然後變成了一些蛋白質和核酸。我們會感覺有何不同嗎?其實不會的。 如果我們假設我們的整個意識狀態都是由物理定律決定的,那麽由於物理定律本身的對稱性,時間反演中,我們自身的記憶也會隨之原樣不變地反演回去。
比如說,我現在處於不惑之年,我有的大腦中儲存的記憶包含了一系列事件的序列:從一端的童年、少年、戀愛、大學、結婚、工作、生女,一直到另一端的端點:正在寫一篇關於時間箭頭的文章。我們說,如果時間是「正流」的,這段記憶毫無問題。但是假如時間倒流,我從骨灰開始返回到不惑之年,我的記憶仍然原封不動地回到這個狀態,這才是符合物理定律的。我的記憶中不會出現退休、女兒結婚、抱外孫、彌留這段歷史,因為這才是不符合物理定律的。
那麽,不論是「正流」還是「倒流」,我現在的記憶狀態不會發生什麽變化。 在熵減的世界中,我們記住的是「未來」,而不是「歷史」 。或者說,這僅僅是一個semantics:我們把歷史稱作未來,把未來稱作歷史。如此而已。

從心理學時間來看,我們其實並不知道過去發生了什麽,也不知道未來將要發生什麽,我們只知道 現在我們的記憶狀態 是什麽。而記憶是什麽?記憶是我們觀察者的記憶體在「歷史」上與外界發生相互關系,造就的它「現在」的物理狀態。 我們回憶過去,就是在體驗我們記憶體中現在的狀態 – 是從現在的記憶狀態「反推」出來的歷史狀態。 然而,我們回憶「過去」,從物理定律上來說,也是在回憶「未來」 – 只不過我們把這種回憶叫做「期望」。
也就是說,當我們回味著我們的記憶的時候,我們所能區分的其實不是一個 純粹本體論時間意義上 的絕對的歷史與未來, 我們所能區分的,是兩個相反的時間方向 。正是由於熵增的存在,使得其中一個方向是確定的、唯一的,而另一個方向則是不確定的、開放的。只不過,我們把確定的那一端稱為歷史,把不確定的那一端稱為未來。
真的有一個「流動」的時間嗎?這其實不重要 。除非「時間」這種東西有一種可以超出物理過程而對我們產生真實影響的機制 —— 但是那樣一來,時間也就至少是物理現象之一、並且也滿足物理定律了。
一個流動的時間存在並切實影響了我們的心理?還是說它只是幻象,真實存在的是一段連續的不對稱序列,我們naively地把確定的一端稱作歷史,把不確定的一端稱作未來?這個問題一直縈繞著我。我其實不知道答案。
5、一點點哲學調味品
現在我可以稍微談一下,為何我會避免談及一個「真實」的、「流動著」的時間,而更願意討論直接的物理現象在一個時間維度上的序列。
最直接的原因就是,物理現象是可描述、可計算的,並且能夠對我們發生直接影響的。而脫離物理現象的一個本體論意義上的時間,則更像是一個哲學概念。
即使是在哲學上,相比於「時間維度上的序列」而言,「時間流動」這種圖景存在著某些難以理解的問題。
首先,我們可以問這樣一個問題,既然時間在流動,那麽它的流速是多少?
這個問題多少有些尷尬。一般而言我們談論某種事物的「流速」,我們必須要用時間來度量它。比如說n米/秒,或者是n℃/秒等等。現在我們談論時間的流速,本身暗示了一種自我巢狀,似乎唯一的答案就是1秒/秒?或者是是1?這是什麽意思?「當時間過了1秒鐘,那麽它過了1秒鐘」,這句話根本就不提供任何資訊。既然它不能提供資訊,那麽定義這個「流速」就是完全冗余的。
我們還可以問另外一個問題,既然時間在流動,那麽它有某種性質是在變化的。那麽到底是什麽性質在變化?again,當我們談論「變化」的時候,我們是預設了時間的。但是當我們談論時間本身的變化,就無法處理了。
對時間這件事最著名的哲學分析是McTaggart關於A理論和B理論的論述。這些討論出現在兩篇巨著中,一個是1908年的「The Unreality of Time」, [6] 一個是1927年的「The Nature of Existence」 [7] [8]
關於這一點,請參考我以前的答案
參考
- ^ Carroll, Sean (2010). From Eternity to Here: The Quest for the Ultimate Theory of Time. ISBN 978-0-525-95133-9
- ^ 潘洛斯,1989,皇帝新腦
- ^ E. T.Jaynes, 1965, "Gibbs vs Boltzmann Entropies" American Journal of Physics 33, 391 (1965); doi: 10.1119/1.1971557
- ^ SEP 詞條「chaos」
- ^ arXiv:0706.1347v1
- ^ J. Ellis McTaggart. 「The Unreality of Time.」 Mind 17, no. 68 (1908): 457–74.
- ^ The Nature of Existence (Volume I), 1921. Cambridge: Cambridge University Press.
- ^ The Nature of Existence (Volume II), 1927. Cambridge: Cambridge University Press.










