今天是2022年2月18日,重力子還沒有被發現,所以我們還可以說,重力的本質就是時空的扭曲。在現代重力理論中,「重力」恰恰不是一種「力」,這和初高中階段我們學習的所有東西是矛盾的。
我們先思考一下重力的效果,比如繞著一顆恒星運動的天體,究竟是為什麽會繞著恒星轉動的?在高中階段,我們的解釋是,這個天體受到了恒星的吸引,吸重力提供了向心力,所以天體會做圓周運動。如果我們沒有了「重力」這個概念,這個問題該如何解釋?
我們來看看彎曲時空中物體的運動方程式:
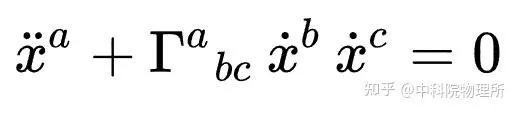
x是(四維)座標,腦袋上加兩個點的是(四維)加速度,加一個點的是(四維)速度。如果 \Gamma 那一項為0,那麽天體的加速度就為0,和不受力的物體完全一樣。對於做圓周運動的天體來說,我們可以說 \Gamma 項讓天體有了加速度——這玩意兒不就妥妥的是「重力」嗎,它起到了重力的效果。只不過在不使用廣義相對論的情況下這個方程式的\Gamma 項長成另一個樣子( F = GMm/r^{2} )而已。
這個\Gamma 叫仿射聯絡(聽起來是一個很酷炫的名字),它描述了向量應該如何被平移。例如下圖1中的,是一個平直時空中的平移,而圖2則描述了是圓面上的平移。
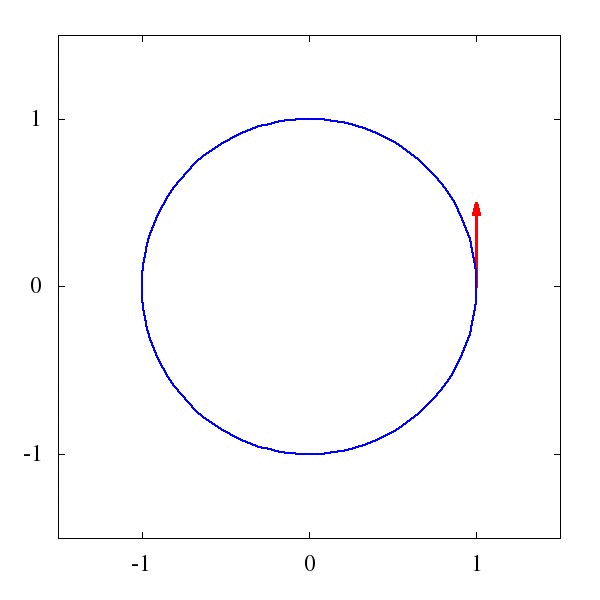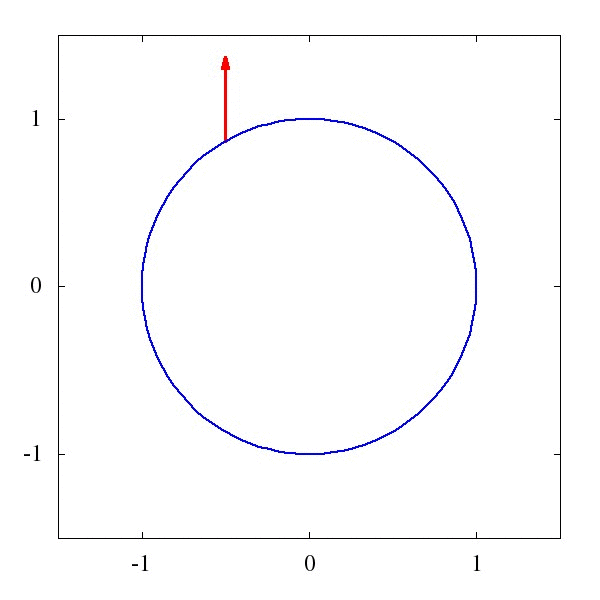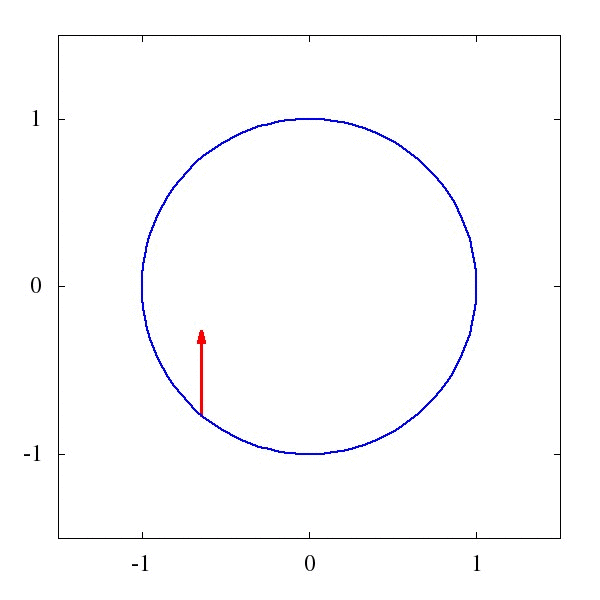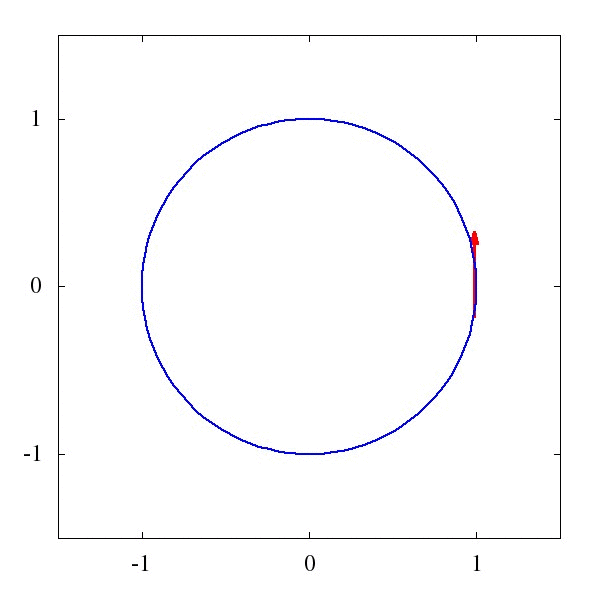
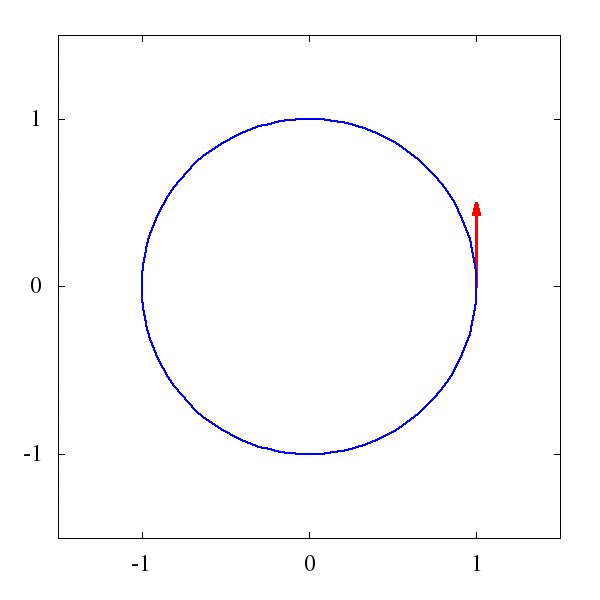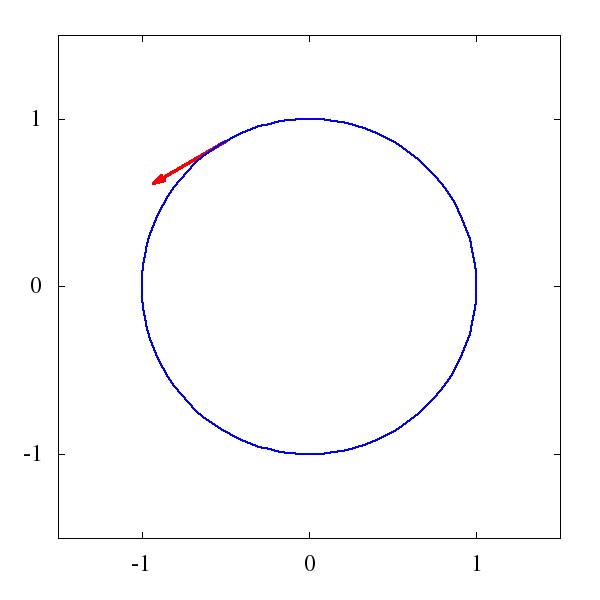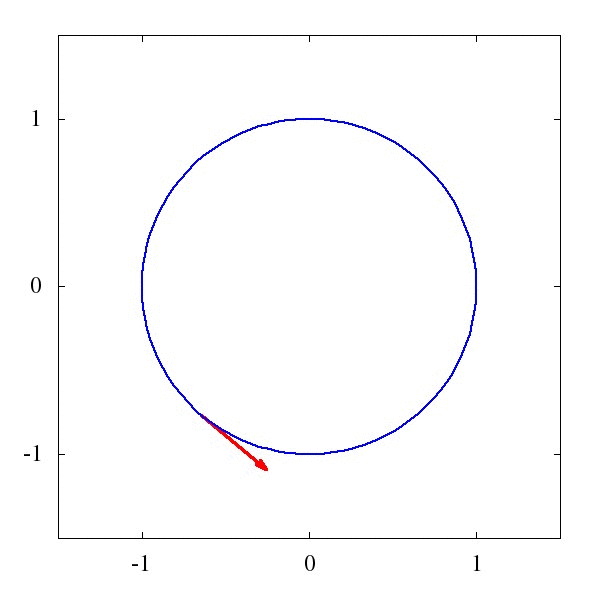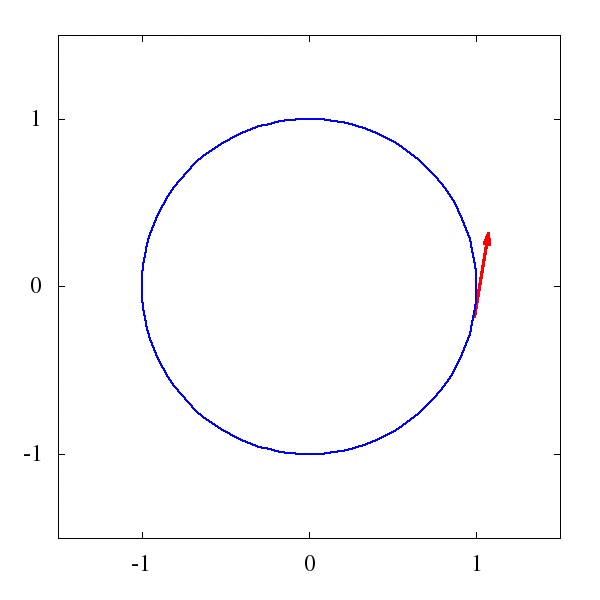
粗略地說,對於均勻平直的座標系,這玩意兒等於0,而對於彎曲的時空和座標系,比如籃球的表面吧,這玩意兒就不為0。某種程度上我們可以說,這個仿射聯絡,就是重力的效應。
那麽這個仿射聯絡是怎麽來的呢?其實仿射聯絡「稍微組合」一下就可以和黎曼曲率R建立起關系:
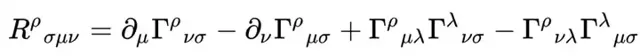
這個R是由質素生成的,它直接刻畫的時空的彎曲,它「稍微組合」就可以是著名的愛因斯坦場方程式
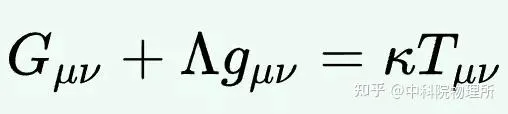
裏面的那個G了。
我們可以看到,相比較於牛頓時代的 ,現代重力理論繞了好大一截。先得弄出來質素,然後得到黎曼曲率,還需要求解仿射聯絡,才能求出重力的效應。看起來實在是麻煩得不行,公式巨復雜,哪裏有科普裏說的「簡單優美」啊!
但是,這恰恰就是現階段人類所理解的重力的本質——時空的扭曲。除了愛因斯坦場方程式,那些奇奇怪怪的公式,都是四維彎曲時空上幾何學的結果。









