第一步:我們來算一算讓電線透過270A的電流持續2秒鐘,它的溫度能達到多少度
這裏我們要用到一個計算式,如下:
\theta _{k} =\frac{1}{\alpha _{0} } [(1+\alpha _{0} \theta _{0} )e^{\frac{\rho _{0} \alpha _{0}t_{k} I_{k}^{2} }{S^2c\gamma } } -1] ,式1
式1中,θk是通電後的最高溫度;θ0是環境溫度;α0是銅的電阻溫度系數,它的值等於0.0043/°C;Ik就是通電電流,Ik=270A;tk就是通電時間,tk=2s;S是導線截面積;c是銅的比熱容,c=390Ws/kg.°C;γ是銅的密度, \gamma=8.9\times 10^3kg/m^3 。
題主並未告知他所處環境的溫度是多少,我們不妨認為就是25°C吧。我們把數據代入到式1中,看看計算結果怎樣:
\theta _{k} =\frac{1}{0.0043 } [(1+0.0043\times 25 )e^{\frac{1.7\times 10^{-8}\times 0.0043\times 2\times 270^{2} }{{(1.5\times 10^{-6})}^2\times 390\times 8.9\times 10^3} } -1]\approx 775.7^\circ C
我們再看題主的說法:「 1.5平方的銅線在持續2秒通270A電流情況下是沒有問題的也無發熱 」,這是不可能的!!!
第二步:我們來算一算導線斷電10分鐘,它的溫度能下降到多少度
我們用到的公式是:
\tau=\tau_me^{-\frac{t}{T}} ,式2
式2中,τ是溫升,就是銅導線表面溫度與環境溫度之差;τm是最高溫升。
註意:當t=4T時,代入到式2中,得到τ=0.0183τw,也即散熱基本完成。可見,計算熱時間常數非常關鍵。
熱時間常數T的定義式如下:
T=\frac{mc}{K_tA} ,式3
熱時間常數運算式中的m是質素,c是材料的比熱容,Kt是綜合散熱系數,A是散熱面積。
理論和實踐都證明,對於某特定的材料,要經過4T的時間它的溫升τ才能上升到穩定溫升τw,溫度達到最高溫度;同理,要經過4T的時間它的溫升才能下降到零,溫度下降到環境溫度。
我們先來計算這根銅導線的熱時間常數T。
由於是裸導線,它的散熱較好,Kt的值取為15W/(m^2°C)。另外,銅導線的兩個端面對散熱起不了多大貢獻,為了計算方便,我們把兩個端面忽略。至於長度嘛,我們就設為2米吧。
因為導線的截面積 S=\frac{\pi D^2}{4} ,我們由此可以計算出直徑D,再進一步計算出截面周長,乘以長度L,就得到表面積A,也就是散熱面積:
A=2\pi L\sqrt{\frac{S}{\pi}}=2\pi\times 2\times \sqrt{\frac{1.5\times 10^{-6}}{\pi}}\approx 8.6832\times 10^{-3}m^2
這段電線的質素: m=SL\gamma=1.5\times 10^{-6}\times 2\times 8.9\times 10^3\approx0.0267kg
我們由此就可以計算出熱時間常數T:
T=\frac{mc}{K_tA}=\frac{0.0267\times 390}{15\times 8.6832\times 10^{-3} }\approx80.0s
我們由此知道,對於題主的截面積1.5平方毫米長度為2米的銅導線來說,當t=4T=4x80=320s時,溫升就降到很小的值,我們代入數據證明一下:
\tau=\tau_me^{-\frac{t}{T}}=775.7e^{-\frac{4T}{T}}\approx 14.21K
我們把它加上環境溫度θ0=25°C,得到:
\theta=\tau+\theta_0=14.21+25=39.21^\circ C
這就是答案:當停止通電後320秒,導線的溫度由775.7度下降到39.21度。當10分鐘時,溫度則下降到25.43度,與環境溫度的偏差人體已經感覺不出來了。
給題主提個問題
題主的疑問:「有沒有計算一根電線1秒內可以最高承受多大電流?」。
如何計算?很簡單,銅導體的最高溫升在國家標準中是60K,我們由下式即可算出該裸導線允許透過的電流值:
I=\sqrt{\frac{K_tM\tau S}{\rho}} ,式4
式4中,M是導線截面積的周長,τ取值為60,ρ是銅的電阻率,S是導線的截面積,Kt是綜合散熱系數,若有包塑膠層,則它的值比較小,在6到9之間。
題主自己去計算把。
既然題主向大家提問,我回答了題主的問題,我反過來問題主一個問題:為何式4中沒有導線長度?事實上,我們在查電工手冊的導線載流量表時,也會發現導線的載流量與長度無關,為何?
看了幾個評論,各有各的說法,甚至連開腦洞都有。我給出正解吧。
我們看下圖:
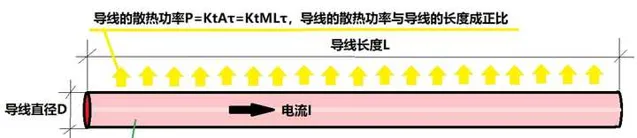
我們從上圖中看到,當導線的溫升進入穩態後,導線的散熱既可以從它長度方向的表面散熱,也可以從兩個端面散熱。但我們知道導線的長度遠遠大於端面直徑,因此端面的散熱可以忽略不計。
我們看到導線的發熱功率為: P_1=I^2R=I^2\rho\frac{L}{S} ,式5
也就是說,導線的發熱功率與導線的長度L成正比。
再看導線的散熱。
當導線的溫升進入穩態後,導線的散熱功率為: P=K_tA\tau=K_tML\tau ,式6
我們看到, 導線的散熱同樣與導線的長度成正比。
導線在穩態條件下,導線自身溫度升高值等於零,它消耗的熱功率當然也等於零。於是,導線的發熱功率等於導線的散熱功率。因此我們有:
I^2\rho\frac{L}{S}=K_tML\tau ,式7
我們把式7等號左右兩側的長度L刪去,稍加變形後,就得到: I=\sqrt{\frac{K_tM\tau S}{\rho}} 。
這就是式4,我們從中看到導線載流量與導線長度無關的原因。
看到某位知友說式1中的溫度θ要用克耳文溫標,這是不對的,這裏的θ是攝氏度溫標。
我們知道,導線流過電流I後會發熱,但由於電流存在的時間很短,只有2秒,類似於短路,它的散熱等於零,類似於絕熱過程。如此一來,我們有:
I_k^2\rho_0(1+\alpha\theta)\frac{L}{S}dt=c\gamma SLd\theta
其中等號左邊就是導線在dt時間段內產生的熱量,而等號右邊則是導線溫度上升所消耗的熱量,其中dθ就是溫度的改變量。註意,這裏的dθ的單位是攝氏度,而電阻溫度系數α的單位是1/°C,不是克耳文溫標。
我們從上式中積分求出θ,就得到了式1: \theta _{k} =\frac{1}{\alpha _{0} } [(1+\alpha _{0} \theta _{0} )e^{\frac{\rho _{0} \alpha _{0}t_{k} I_{k}^{2} }{S^2c\gamma } } -1] ,與克耳文溫標一點關系也沒有。
另外,有知友提問:與集膚效應有關嗎?
回答是:如果導線的直徑較大,例如導線的半徑超過50Hz交流電的穿透深度b=8.3mm,則必須考慮集膚效應的影響。此時式1變成如下形式:
\theta _{k} =\frac{1}{\alpha _{0} } [(1+\alpha _{0} \theta _{0} )e^{\frac{K_f\rho _{0} \alpha _{0}t_{k} I_{k}^{2} }{S^2c\gamma } } -1]
註意,在指數項的分子部份,多了一個Kf,Kf叫做交流附加系數。在一般情況下,50Hz交流電的Kf=1.05,故可忽略不計。
對於題主的導線,截面積僅僅才1.5平方,故無需考慮集膚效應的影響。










