之前寫過不少關於微分和導數的文章:
今天這篇文章再換一個角度來談論微分和導數,讓我們從微分出現的原因說起。
1 微分出現的原因
出於種種原因,我們可能想去求曲線的長度、曲面梯形的面積:
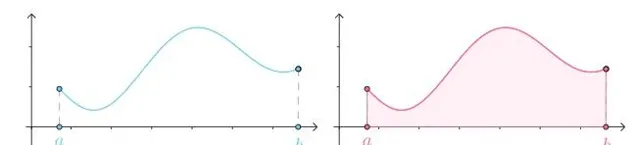
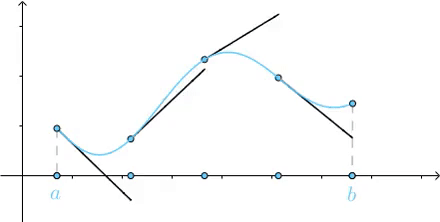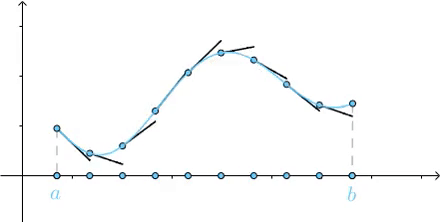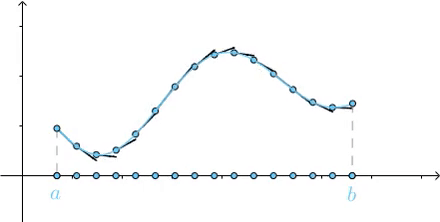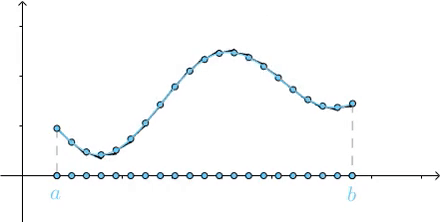
求解思路是這樣的,以求曲線長度為例,將曲線分為多個部份,每一部份都用切線來近似曲線:
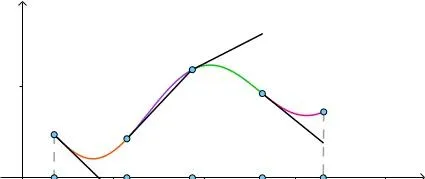
劃分的越細,直到劃分為無窮多份,最終這些切線的長度加起來就是曲線的長度:
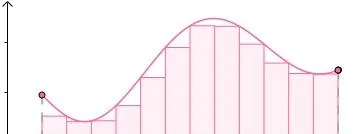
求曲邊梯形面積也是類似的,用小矩形來近似曲邊梯形的面積,隨著小矩形的增多最終得到曲邊梯形的面積:
上面的思想就是微積分的核心思想,「以直代曲」。曲線長度、曲邊梯形就是「曲」,切線、小矩形就是用來近似(代替)的「直」,這種「直」就是 微分 。關於這裏還不了解的可以看「微分是什麽?」這篇文章。
2 微分與導數
先不談曲邊梯形,本節先來回答曲線的微分是什麽,也就是可以近似曲線的直線是什麽?
2.1 幾何分析
下面結合幾何來理清一下求解的思路。假設有曲線f(x) 和直線g(x) ,如果兩者完全相等,那麽有:
f(x)=g(x)\quad 或\quad f(x)-g(x)=0\\
很顯然這在整個曲線和直線上是做不到的,但肯定可以做到在某點上相等,比如讓它們在x_0 點相等,從幾何上看就是曲線f(x) 和直線g(x) 在x_0 點相交:

下面要更進一步,不過不要太貪心,只希望兩者在x_0 附近盡量相等。比如像下圖一樣,在(x_0-\Delta x,x_0+\Delta x) 的區間內,曲線f(x) 和直線g(x) 相差很小:
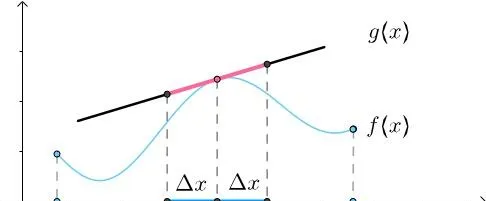
這點如果可以做到,那就可以按照上一節說的,將曲線分成n份,每份都用各自的微分來近似。
2.2 代數分析
透過幾何分析,思路已經理清楚了,要找的微分(直線)需要滿足以下兩點:
(1)曲線f(x) 和直線g(x) 要交於x_0 點。假設直線g(x) 的斜率為k ,那麽根據點斜式,可得直線函數:
g(x)=f(x_0)+k(x-x_0)\\
這裏面就是k 還未知,求出了k 就得到了想要的直線,也就得到了微分。
(2)曲線f(x) 和直線g(x) 要在(x_0-\Delta x,x_0+\Delta x) 的區間內盡可能相等。用代數表示即為:
f(x)-g(x)\approx 0,\quad x\in(x_0-\Delta x,x_0+\Delta x)\\
有約等號的式子是沒法計算的,引入高階無窮小o(\Delta x) 可以將約等號去掉:
f(x)-g(x)=o(\Delta x),\quad x\in(x_0-\Delta x,x_0+\Delta x)\\
高階無窮小o(\Delta x) 的意思就是在\Delta x 這個範圍內無限的接近於 0。至於為什麽它無限接近於 0,以及為什麽是高階無窮小,在文章的最後會進行補充說明。
2.3 解出直線的斜率 k
經過上面的分析我們有了:
\left.\begin{aligned} g(x)=f(x_0)+k(x-x_0)\\ f(x)-g(x)=o(\Delta x) \end{aligned}\right\}\implies f(x)-f(x_0)-k(x-x_0)=o(\Delta x) \\
這已經足夠讓我們解出直線的斜率k 了。註意到\Delta x=x-x_0 ,可以進行如下變形:
\begin{aligned} f(x)-f(x_0)-k(x-x_0)=o(\Delta x) &\implies f(x)-f(x_0)-k\Delta x=o(\Delta x)\\ &\implies \frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=\frac{o(\Delta x)}{\Delta x} \end{aligned} \\
兩側取極限可得:
\lim_{\Delta x\to 0}\frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=\lim_{\Delta x\to 0}\frac{o(\Delta x)}{\Delta x}\implies \lim_{\Delta x\to 0}\frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=0 \\
略微作一下化簡可得:
k=\lim_{\Delta x\to 0}\frac{f(x)-f(x_0)}{\Delta x}\\
至此我們就求出了k ,也就找到了f(x) 的 微分 (直線g(x) 的形式還需要變一下才是真正的微分,關於這點可以參考「dx,dy是什麽?」這篇文章)。
這個k 在微積分中又有一個專門的名字,稱為f(x) 的 導數 。k 如果存在(因為k 是透過極限求得的,這個極限有不存在的可能),那麽就稱f(x) 可導。
上面的思路還可以進一步思考,如果要找最接近曲線f(x) 的多項式曲線呢?這會得到泰勒公式,就留給大家作課後習題吧。
3 補充說明
這裏補充說明兩點:
(1)高階無窮小o(\Delta x) 為什麽表示在(x_0-\Delta x,x_0+\Delta x) 的區間內無限接近於 0 ?這是因為它滿足:
\lim_{\Delta x\to0}o(\Delta x)=0\\
上面這個極限式意味著\Delta x 越小,也就是越接近於x_0 點,o(\Delta x) 越接近於 0。用動畫表示就是:
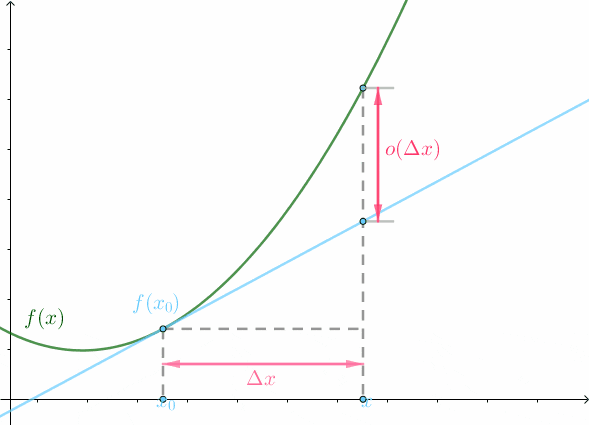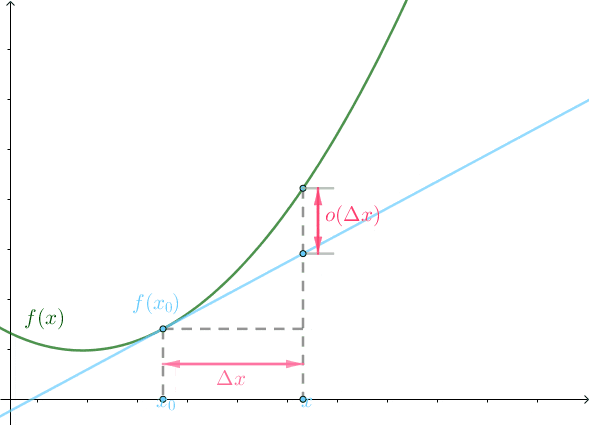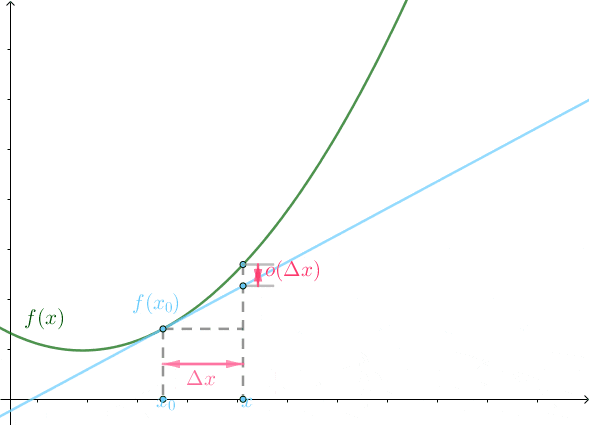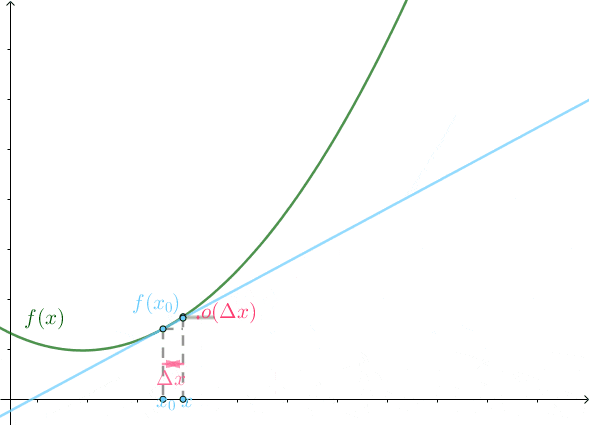
上圖中綠線就是曲線f(x) ,藍線為微分,可以看到隨著\Delta x 縮小,兩者之間的距離o(\Delta x) 也無限接近於 0。
(2)為什麽一定要高階無窮小?同階無窮小行不行?關於這點可以參考「為什麽算出來的圓周率 π 等於 4 ?」這篇文章。
更多內容推薦 馬同學圖解數學 系列








