回答這個問題,需要從抽象的角度理解: 大部份機械結構都處於穩定平衡態,所以在雜訊(敲一敲)的作用下,會回到平衡態(設計狀態)。
我們討論穩定平衡的時候,都會要問一個問題: 這是在什麽變量空間下的平衡?
一個球,在鍋底穩定平衡,那是在真實空間上的平衡,也就是 x,y 發生變化的時候,也能平衡。
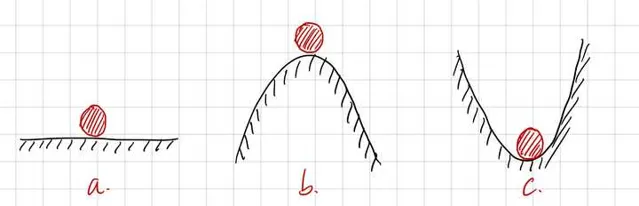
上圖就是三種平衡態,其中c就是穩定平衡,而b就是不穩定平衡。它們之間的差別在於:穩定平衡在外界擾動之後,是可以回到原先狀態的;而不穩定平衡則不會,比如b中的球就會墜落山下。
而這裏說的機械結構, 對應的空間則更大 ,是描述機械形狀的空間。你可以這樣理解: 空間中的每一個點都對應一個機械結構,兩點之間的距離則代表了變化的差異。這個空間是無窮維的。
如果有一點點變化的話,那在這個空間裏看,機械所處的位置就發生了一個微小的變化。
對於大部份的物體,比如就是鐵棍吧,彎了一點點,它一定會有恢復的力。也就是一個負反饋。
從能量的角度看,只要不是範性形變,那在這個無窮維空間的大部份位移都會增加系統的能量。
從而可以認為這個系統是穩定平衡的。
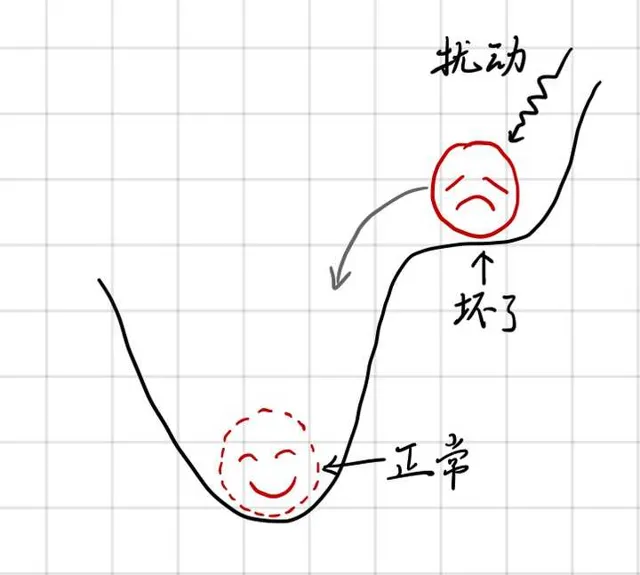
再用一張圖來解釋「敲一敲」這個過程:
舉個例子,如果兩個齒輪這樣卡在了一起:

我們稱之為「故障狀態」,那麽 這個形變就會帶來彈性勢能的增加 ,所以在很多變化的維度上(比如齒輪旋轉), 這個狀態是不穩定的 。 只要敲一敲,齒輪發生了微小的旋轉,那它立刻就會回到低能態(也就是正常狀態)。
那麽為什麽說,大部份機械結構,都處於穩定平衡的狀態呢?因為微擾是不可避免的,只有穩定平衡才是實用的狀態。
然後就是另一個問題了,為什麽有的結構,敲一敲就不行了呢?比如軟件出了bug、檔損壞了,為什麽就不能用這個方法了呢?
有三點可能:
- 檔的「損壞」狀態,對應的能量並不比未損壞的狀態高。所以在微擾下不會自發回到某個狀態;
- 「敲一敲」的能量太低了,不足以在那麽小的尺度上引發變化。
- 有的雖然是機械結構,但敲擊引發的雜訊只能影響少部份維度。也就是敲擊對應的震動模式並不能影響到很多維度,而能影響到的維度則不是穩定平衡。
補充一點,從控制論的角度看,大部份機械結構在極少數特定的維度上,其能量曲線是非常平的。這是為了保證機械結構對外界能夠做出反應。但這與一開始說的並不矛盾,因為這只是少數幾個維度。
文章/回答精選集:
復雜性科學 - 生活×物理 - 藝術×數理 - 科研評論
公眾號/微博: 「復雜魚塘」,complex-zyb
Bilibili: 復雜魚塘
【相關回答】:










