基於格的難題你只說了一個RLWE,不知你是不是已經了解基於格的其它難題。參照剛才在另外一個問題中的回復。
密碼學難題還有很多。說幾個比較熱門的。基於格的密碼難題 \rm SVP
和 \rm CVP
,這兩個難題都是抗量子的。還有基於他們構建的LWE和RLWE問題,它們是構建全同態加密的基礎。
相關的知識內容可關註我並去我專欄學習。
下面我們來講下基本的\rm SVP
和 \rm CVP
。
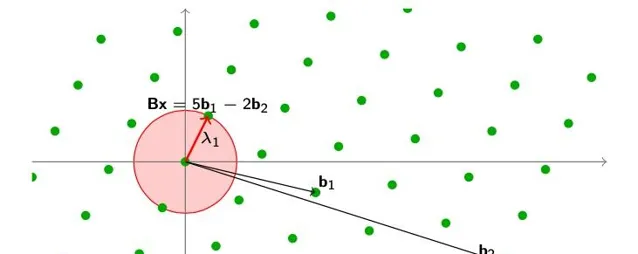
最短向量問題 \rm SVP
讓我們定義最基本的涉及格的計算難題:最短向量問題,簡稱 \rm SVP
。 在這裏,我們給出了一個格,需要我們找到最短的非零格點。 更準確地說,\rm SVP
有三個變體,這取決於我們是否必須實際找到最短的向量,找到它的長度,或者僅僅取決於它是否比某些給定的數碼小:
Search
\rm SVP
: 給定格基 B∈\mathbb{Z}^{m×n}
求 v∈\mathcal{L}(B)
,使 ||v||=λ_1(\mathcal{L}(B))
。
Optimization
\rm SVP
: 給定格基 B∈\mathbb{Z}^{m×n}
,找到 λ_1(\mathcal{L}(B))
。
Decisional
\rm SVP
:給定格基 B∈\mathbb{Z}^{m×n}
和有理數 r\in \mathbb{Q}
,判斷λ_1(\mathcal{L}(B))\leq r
是否成立。
註意,我們限制格基由整數向量組成,而不是任意的實向量。這樣做的目的是使輸入以有限的多位表示,這樣我們就可以將 \rm SVP
視為一個標準的計算難題。我們還可以允許格基由有理向量組成。這將導致一個本質上等價的定義,因為透過縮放,可以使所有有理數座標都是整數。
上述三個變體之間的兩個簡單關系是,決策變體不比最佳化變體更難,最佳化變體不比搜尋變體更難。 事實上,可以證明逆向也是正確的:最佳化變量不比決策變量更難,搜尋變量不比最佳化變量更難。 總之,這三個變體本質上是等價的。
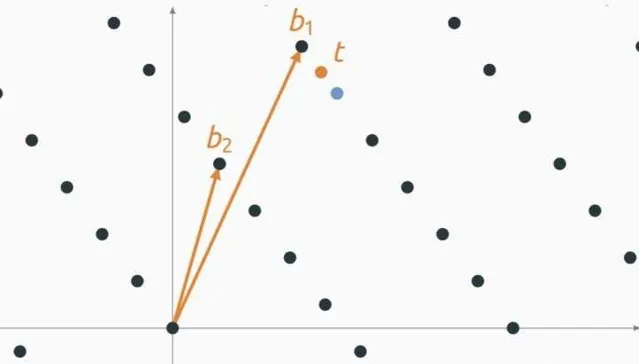
最近的向量問題 \rm CVP
另一個基本格難題是最近的向量問題,簡稱 \rm CVP
,i.e.,目標是找到最接近給定空間點的格點。 和以前一樣,對於任何近似因子 \gamma \geq 1
,我們可以定義三個變體:
Search
\rm CVP_\gamma
: 給定格基 B∈\mathbb{Z}^{m×n}
和向量 t\in \mathbb{Z}^{m}
,尋找 v\in \mathcal{L(B)}
使得 ||v-t|| \leq \gamma \cdot {\rm {dist}} (t, \mathcal{L}(B))
。
Optimization
\rm CVP_\gamma
:給定格基 B∈\mathbb{Z}^{m×n}
和向量 t\in \mathbb{Z}^{m }
,求 d
使d≤{\rm dist}(t,\mathcal{L}(B))≤\gamma\cdot d
。
Promise
\rm CVP_\gamma
: 由 a triple (B,t,r)
給出一個難題例項,其中 B∈\mathbb{Z}^{m×n}
是格基, t∈\mathbb{Z}_m, r∈\mathbb{Q}
。 在 YES 例項中, {\rm dist}(t,\mathcal{L}(B)≤r
。在沒有情況下, {\rm dist}(t,\mathcal{L}(B)\geq r
。
\rm CVP
和 \rm SVP
都是困難的計算問題,我們將在本課程後面更詳細地討論這些問題。 還有一些格中容易計算的問題,如:
Membership
: 給定格基 B∈\mathbb{Z}^{m×n}
和向量 v\in \mathbb{Z}^{m}
,decide v
是否屬於 \mathcal{L}(B)
。 方程式 Bx=v
可以看作是 n
個變量中的 m
線性方程式組。 因此,我們可以透過高斯消除來有效地解決它。 如果一個解存在,並且它恰好在 \mathbb{Z}^n
(as opposed to \mathbb{Q}^n
)中,則輸出YES;否則輸出NO。
Equivalence
: 給定格基 B_1, B_2∈\mathbb{Z}^{m×n}
, decide if \mathcal{L}(B_1) = \mathcal L(B_2)
。 為了解決這個問題,我們檢查了兩件事: B_1
的每一列都包含在 \mathcal L(B_2)
中, B_2
的每一列都包含在 \mathcal L(B_1)
中。 如果 \mathcal{L}(B_1) = \mathcal L(B_2)
,則滿足這兩個檢查。 相反,如果滿足這些檢查,則 \mathcal{L}(B_1) \subseteq \mathcal L(B_2)
和 \mathcal{L}(B_1) \supseteq \mathcal L(B_2)
,因此 \mathcal{L}(B_1) = \mathcal L(B_2)
。