兩個算符對易，應該怎麽去理解？

我在評論區裏提到力學量的對易子一般都是純虛數, 這個結論好像意外地有一部份人沒聽過?

其實吧, 更嚴格一點的說法是厄米算符對易子一定是反厄米的, 這不是啥經驗之談, 可以輕松證明:

\[\begin{align} & \ \ \ \ \ \ \ \text{set}\ H_{1}^{\dagger }={{H}_{1}},H_{2}^{\dagger }={{H}_{2}} \\ & \Rightarrow {{\left[ {{H}_{1}},{{H}_{2}} \right]}^{\dagger }}={{\left( {{H}_{1}}{{H}_{2}} \right)}^{\dagger }}-{{\left( {{H}_{2}}{{H}_{1}} \right)}^{\dagger }}={{H}_{2}}{{H}_{1}}-{{H}_{1}}{{H}_{2}}=-{{\left[ {{H}_{1}},{{H}_{2}} \right]}^{\dagger }} \\ & \Rightarrow \left[ {{H}_{1}},{{H}_{2}} \right]\ \text{is}\ \text{an}\ \text{anti-hermitian}\ \text{stuff}\text{.}\ \\ \end{align}\]

看 tag 都是物理方向的, 那麽我這裏總結一下從量子力學角度的理解:

我們都知道任意兩個算符 A,B 的測量具有不確定性關系 \[\Delta A\Delta B\ge \frac{1}{2}\left| \left\langle \left[ A,B \right] \right\rangle \right|\]

所以當我們看到兩個算符可對易的時, 我們想到的應該是二者對應的物理量可以同時被精準測量. ^[1]

這等價於說存在一些量子態即是 A 的本征態又是 B 的本征態.

一般而言我們研究的都是厄米算符, 所以更進一步來說就是:

"如果兩個厄米算符 A 與 B 對易, 則 A 與 B 的共同本征矢構成態空間的一個正交歸一基. "

厄米算符的本征矢本來就有完備性, 即這個命題重點在於:

\[\left[ A,B \right]=0\Rightarrow \] 二者存在一組共同的本征矢.

結論的證明:

設 \[A\left| u_{n}^{i} \right\rangle ={{a}_{n}}\left| u_{n}^{i} \right\rangle \ \ \ i=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] 其中 i 用於區分同本征值子空間各基矢.

A 是厄米算符 \[\Rightarrow \left\langle u_{n}^{i}|u_{m}^{j} \right\rangle ={{\delta }_{mn}}{{\delta }_{ij}}\] ----------------------------------------------[i]

\[\left[ A,B \right]=0\Rightarrow AB\left| u_{n}^{i} \right\rangle =BA\left| u_{n}^{i} \right\rangle ={{a}_{n}}B\left| u_{n}^{i} \right\rangle \]

說明 \[B\left| u_{n}^{i} \right\rangle \] 也是 A 的本征矢, 且處於 \[{{a}_{n}}\] 對應的本征子空間 ^[2] ------------------------[ii]

下面討論在 A 的本征矢表象下的 B 矩陣 (即 B 的矩陣元 \[B_{mn}^{ij}=\langle u_{m}^{i}|B\left| u_{n}^{j} \right\rangle \] ):

(不懂矩陣表示的看這 正樹：表象變換的么正算符怎麽定義的? 為何說算符與態可以看作矩陣?)

結合 [i][ii] 不難得到: \[m\ne n\Rightarrow B_{mn}^{ij}=\langle u_{m}^{i}|B\left| u_{n}^{j} \right\rangle =0\]

這說明 B 是一個分塊對角的矩陣:

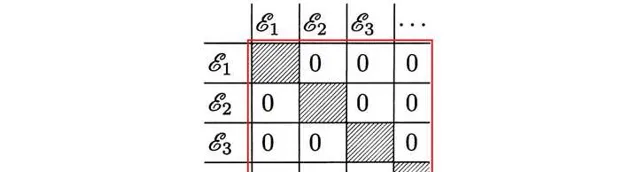
其中 \[{{\varepsilon }_{n}}\] 代表 \[{{a}_{n}}\] 的本征子空間即 \[\left| u_{n}^{i} \right\rangle \ \ \ i=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] 張成的空間.

而陰影部份就是我們接下來要討論的部份了:

(1). 若 A 的本征值非簡並, 即 \[{{g}_{n}}\equiv 1\] , 每個格子都是\[1\times 1\] 的矩陣, 這就說明上面這個矩陣就是個對角陣. 此時標註簡並情況的 i 可以去掉, \[\left| u_{n}^{i} \right\rangle =\left| {{u}_{n}} \right\rangle \] 就是 \[B\] 的本征矢.

(2). 若 A 的本征值存在簡並, 則圖中的每個陰影子塊都是一個 \[{{g}_{n}}\times {{g}_{n}}\] 的方陣, 其中的矩陣元表示為 \[B_{nn}^{ij}=\langle u_{n}^{i}|B\left| u_{n}^{j} \right\rangle \] 其中 \[i,j=1,2,3,\cdot \cdot \cdot ,{{g}_{n}}\] . B 是厄米算符, 所以這個子塊也是厄米矩陣, (即 \[{{\left( B_{nn}^{ji} \right)}^{*}}=B_{nn}^{ij}\] ), 這說明這個矩陣一定可以對角化, 對角化的過程無非就是在子空間內尋找一組新的向量做基使得這組基中表示的 B 矩陣是對角陣. 仿照 (1) 中的過程不難發現所有的新向量都是 B 在 \[{{\varepsilon }_{n}}\] 中的本征矢. 各個子空間中的所有新向量的集合即為所求的一組完備的共同本征矢, 即這些新向量同時是 A 與 B 的本征矢.

♦\text {Q:} 前面說了若 A 與 B 可對易, 就可以找到一組共同的本征矢, 那麽難道不可對易就一定不能找到一組共同的本征矢嗎？

♦\text {A:} 是的,下面用反證法予以證明:

假定算符 A 與 B 不可對易. 但我就是 somehow 找到了他們的一組共同本征矢 \[\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 使得 \[A\left| {{a}_{n}},{{b}_{n}},i \right\rangle ={{a}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 且 \[B\left| {{a}_{n}},{{b}_{n}},i \right\rangle ={{b}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 其中 i 標註簡並情況.

那麽就有 \[\left( AB-BA \right)\left| {{a}_{n}},{{b}_{n}},i \right\rangle =AB\left| {{a}_{n}},{{b}_{n}},i \right\rangle -BA\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] \[\begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =A{{b}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle -B{{a}_{n}}\left| {{a}_{n}},{{b}_{n}},i \right\rangle \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\left( {{a}_{n}}{{b}_{n}}-{{b}_{n}}{{a}_{n}} \right)\left| {{a}_{n}},{{b}_{n}},i \right\rangle =0 \\ \end{align}\]

由於 \[\left| {{a}_{n}},{{b}_{n}},i \right\rangle \] 不能全是零向量, 所以只能是 \[AB-BA=\left[ A,B \right]=0\]

這就與前提矛盾了, 所以, 你不能.

我們一般利用這個特性來構造可對易觀察算符的完全集合 ^[3] .

如果覺得上面那些實在有些抽象心裏沒底的話可以看看下面這個:

參考

1. ^ 如果有對應的物理量的話
2. ^ 厄米陣的不同本征子空間都是相互正交的.
3. ^ 有些地方稱之為力學量完全集