授人以魚不如授人以漁,這篇文章會介紹 如何透過「統計學檢驗」來對比機器學習演算法效能 。掌握了這個方法後,我們就不需要再人雲亦雲,而可以自己分析演算法效能。
首先結論如下,在對比 兩個演算法 在 多個數據集 上的表現時:
在對比 多個演算法 在 多個數據集 上的表現時:
文章結構如下:(1-2) 演算法對比的原因及陷阱 (3-4) 如何對比兩個演算法 (5-6)如何對比多個演算法 (7)如何根據數據特性選擇對比方法 (8)工具庫介紹。
1. 為什麽需要對比演算法效能?
統計學家George Box說過:「All models are wrong, but some are useful」(所有模型都是錯誤,只不過其中一部份是有價值的)。通俗來說, 任何演算法都有局限性,所以不存在「通用最優演算法」,只有在特定情境下某種演算法可能是漸進最優的 。
因此,評估演算法效能並選擇最優演算法是非常重要的。不幸的是,統計學評估還沒有在機器學習領域普及,很多評估往往是在一個數據上的簡單分析,因此證明效果有限。
2. 評估演算法中的陷阱
首先我們常說的是要選擇一個 正確的評估標準 ,常見的有:準確率(accuracy)、召回率(recall)、精準率(precision)、ROC、Precision-Recall Curve、F1等。
選擇評估標準取決於目的和數據集特性。在較為平衡的數據集上(各類數據近似相等的情況下),這些評估標準效能差別不大。而在數據嚴重傾斜的情況下,選擇不適合的評估標準,如準確率,就會導致看起來很好,但實際無意義的結果。舉個例子,假設某稀有血型的比例(2%),模型只需要預測全部樣本為「非稀有血型」,那麽準確率就高達98%,但毫無意義。在這種情況下,選擇ROC或者精準率可能就更加適當。這方面的知識比較容易理解,很多科普書都有介紹,我們就不贅述了。
其次我們要正確理解 測量方法 ,常見的有
舉個例子,我們想要分析刷知乎時間(每天3小時 vs. 每天10小時)對於大學生成績的影響。如果我們使用相同的20個學生,觀察他們每天3小時和10小時的區別,那就是重復測量。如果我們選擇40個學生,分成兩組每組20人,再分別觀察那就是獨立測量。如果我們先找20個學生,再找20個和他們非常相似的大學生,並配對觀察,就是成對相似。
我們發現,當錯誤的理解測量方式時,就無法使用正確的統計學手段進行分析 。
在這篇文章中我們預設:評估不同演算法在多個 相同數據集 上的表現屬於 重復測量 ,而特例將會在第七部份討論。同時,本文介紹的方法 可以用於對比任何評估標準 ,如準確度、精準度等,本文中預設討論準確度。
3. 兩種演算法間的比較:不恰當方法

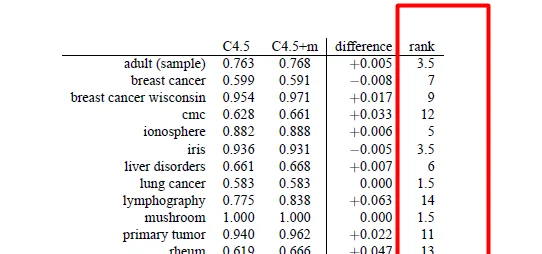
圖1展示了兩種決策樹方法(C4.5,C4.5+m)在14個數據集上的準確率。那麽該如何對比兩種演算法呢?先說幾種錯誤(不恰當)的方法:
不恰當方法1:求每個演算法在所有數據集上的均值,並比較大小 。錯誤原因:我們對於演算法在不同數據集上錯誤的期望不是相同的,因此求平均沒有意義。換句話說,數據不符合相稱性(commensurate)。
不恰當方法2 : 進行配對樣本t檢測(Paired t test) 。顯然,t test是統計學方法,可以用來檢視兩種方法在每個數據上的平均差值是否不等於0。但這個方法不合適原因有幾點:
不恰當方法3:符號檢驗(sign test) 是一種無參數(non-parametric)的檢驗,優點是對於樣本分布沒有要求,不要求正態性。比較方法很簡單,就是在每個數據集上看哪個演算法更好,之後統計每個演算法占優的數據集總數。以這個例子為例,C4.5在2個數據集上最優,2個平手,10個最差。如果我們對這個結果計算置信區間,發現p<0.05需要至少在11個數據集上表現最優。因此這個方法的缺點有:

4. 兩種演算法間的比較:推薦方法
考慮到通用性,我們需要使用非參數檢驗。換句話說,我們需要保證對樣本的分布不做任何假設,這樣更加通用。
方法1:Wilcoxon Signed Ranks Test(WS ) 是 配對t檢驗的無參數版本 ,同樣是分析成對數據的差值是否等於0,只不過是透過排名(rank)而已。換個角度看,我們也可以理解為 符號檢驗的定量版本 。優點如下:
方法2(詳見第七部份):Mann Whitney U test (MW)和WS一樣,都是無參數的且研究排名的檢驗方法。MW有以下特性:
換句話說,MW是當樣本量不同時才建議勉強一試,因為不符合獨立測量的假設。不同數據集的錯誤(準確率)不一定符合特定分布,很可能不符合相稱性,但在特定情況下有用,詳見第七部份。
總結:如果樣本配對且符合正態分布,優先使用配對t檢測。如果樣本不符合正態分布,但符合配對,使用WS。如果樣本既不符合正態分布,也不符合配對,可以嘗試MW。
5. 多種演算法間的比較:不恰當的方法
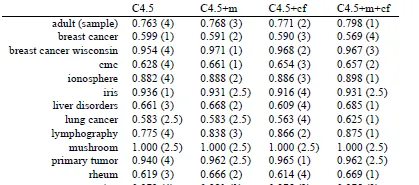
圖4提供了四種演算法(C4.5,C4.5+m,C4.5+cf,C4.5+m+cf)在14個數據集上的準確率。
不恰當方法1 :一種看法是,我們是否可以把兩個演算法的對比推廣到多個演算法上。假設有k個演算法,我們是否可以對它們進行兩兩比較,經過 \frac{(1+(k-1))\times (k-1)}{2}=\frac{k^2-k}{2} 次計算得到一個矩陣。這個是經典的多元假設檢驗問題,這種窮舉法一般都假設了不同對比之間的獨立性,一般都不符合現實,需要進行校正,因此就不贅述了。
不恰當方法2 : Repeated measures ANOVA 是經典的統計學方法,用來進行多樣本間的比較是,可以看做是t檢驗的多元推廣。ANOVA不適合對比演算法表現的原因如下:
不幸的是,我們想要對比的演算法表現不符合這個情況,因此ANOVA不適合。
6. 多種演算法間的比較:推薦的方法
我們需要找到一種方法同時解決第5部份中提到的問題,這個方法需要:
Demšar [1]推薦了非參數的多元假設檢驗 Friedman test 。Friedman也是一種建立在排名(rank)上的檢驗,它假設所有樣本的排序均值相等。具體來講,我們首先給不同演算法在每個數據集上排序,並最終計算演算法A在所有數據集上排名的均值。如果所有演算法都沒有效能差別,那麽它們的效能的平均排名應該是相等的,這樣我們就可以選擇特定的置信區間來判斷差異是否顯著了。
假設我們透過Friedman test發現有統計學顯著( p <0.05),那麽我們還需要繼續做事後分析(post-hoc)。 換句話說,Friedman test只能告訴我們演算法間是否有顯著差異,而不能告訴我們到底是哪些演算法間有效能差異。想要定位具體的差異演算法,還需要進行post-hoc分析。
Friedman test一般配套的post-hoc是Nemenyi test,Nemenyi test可以指出兩兩之間是否存在顯著差異。我們一般還會對Nemenyi的結果視覺化,比如下圖。

另一個值得提的是,即使Friedman證明演算法效能有顯著不同,Nemenyi不一定會說明到底是哪些演算法間不同,原因是Nemenyi比Friedman要弱(weak),實在不行可以對必須分析的演算法成對分析。
方法2(詳見第七部份):和兩兩對比一樣,在多個樣本對比時也有一些特定情況導致我們不能使用Friedman-Nemenyi。另一個或特許以值得一試的無參數方法是Kruskal Wallis test搭配Dunn's test(作為post-hoc)。 這種方法的特點是:
7. 再看重復測量和獨立測量
我們在第二部份分析了重復測量與獨立測量,而且假設機器學習效能的對比 應該是建立在「重復測量」上的,也就是說所有的演算法都在相同的數據集上進行評估 。
在這種假設下,我們推薦了無參數的:Wilcoxon對兩個演算法進行比較, Friedman-Nemenyi對多個演算法進行對比。
然而,「 重復測量」的假設不一定為真 。舉個例子,如果我們只有一個數據,並從數據中采樣(sample)得到了很多相關的測試集1, 2,3...n,並用於測試不同的演算法。
在這種情況下,我們就可以用Mann Whitney U test對比兩種演算法,Kruskal-Dunn對比多種演算法。 而且值得註意的是,這種情況常見於人工合成的數據,比如從高斯分布中采樣得到數據 。因此,要特別分析數據的測量方式,再決定如何評估。
8. 工具庫與實作
我們知道R上面有所有這些檢驗,著重談談Python上的工具庫。幸運的是,上文提到所有檢驗方法在Python上都有工具庫
Scipy Statistical functions :Wilcoxon,Friedman,Mann Whitney
scikit-posthocs:Nemenyi,Dunn's test
文章的配圖來自於[1] 以及我的一篇paper [2],接收後會補上reference。 文章的思路和脈絡基於[1], 建議閱讀。[2]主要著力於特定情況,當重復測量失效時的檢驗。
[1] Demšar, J., 2006. Statistical comparisons of classifiers over multiple data sets. Journal of Machine learning research , 7 (Jan), pp.1-30.
[2] To complete.











