為了稍微系統一點地回答這個問題,也為了整理一下關於四元數的知識,這篇回答分為七個(不均等的)部份:復數與旋轉、四元數的定義、四元數的性質、等距同構、虛四元數的乘積、四元數的共軛作用、共軛作用的效果。
開始了!
一、復數與旋轉
在說四元數與旋轉的關系之前,我們先回顧一下復數與旋轉的關系:
每一個\mathbb{R}^{2} (關於原點)的旋轉都可以用一個復數z_{\theta}=\cos\theta+i\sin\theta 來表示。這是因為,對於每一個點(x,y)=x+iy 來說:
z_{\theta}(x+iy)=(\cos\theta+i\sin\theta)(x+iy)=x\cos\theta-y\sin\theta+i(x\sin\theta+y\cos\theta)
所以z_{\theta} 把(x,y) 移到了(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta) 的位置,也就是旋轉了\theta .
我們還可以把這個過程寫成矩陣形式:
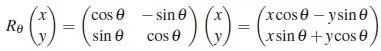
為了更好地看出復數與矩陣的聯系,我們可以把矩陣寫成這樣的形式:
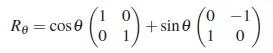
其中,

(順帶說一句,Bourbaki給法國中學生寫的課本中,虛數就是直接這麽定義的。)
於是,我們可以把每個復數都表示成矩陣的形式:
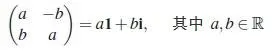
當我們把復數與矩陣結合起來的時候,我們就多了一種描述『和』與『積』等運算的角度。
二、四元數的定義
對於四元數來說,這種『矩陣表示』的方法同樣適用。
每一個四元數q 對應了一個矩陣:
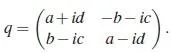
(這並不是四元數與矩陣的唯一對應方法,但這種方法是復數與矩陣對應的推廣。)
【能不寫矩陣形式嗎?】
好吧,把四元數寫成更喜聞樂見的形式就是這樣的:
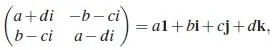
其中,
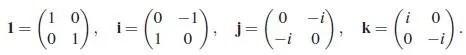
所以四元數就是在復數的基礎上又加了\mathrm{j,k} ,並且同樣地\mathrm{j}^2=\mathrm{k}^2=-1 ,此外還有運演算法則:
\mathrm{ij=k},~\mathrm{jk=i},~\mathrm{ki=j}
\mathrm{ji=-k},~\mathrm{kj=-i},~\mathrm{ik=-j}
這些可以透過矩陣乘法來驗證。(註意,四元數並不滿足乘法交換律!)
我們把四元數空間記作\mathbb{H} ,以紀念其發現者Hamilton。
三、四元數的性質
四元數的很多性質與復數類似,比如:
每一個非零的四元數q 都有逆q^{-1} ,也就是其對應矩陣的逆矩陣。並且有:
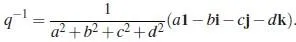
每個四元數q 都有與其共軛的四元數\bar{q} =a1-b\mathrm{i}-c\mathrm{j}-d\mathrm{k} ,並且q\bar{q}=|q|^2 . 其中,q 與\bar{q} 對應的矩陣則是共軛轉置的關系。
定義|q|^{2}=\det q=a^{2}+b^{2}+c^{2}+d^{2} ,所以|q| 就是(a,b,c,d)\in \mathbb{R}^{4} 到原點的距離。
正如單位長度的復數對應了圓(一維球面\mathbb{S}^{1} )一樣,單位長度的四元數滿足a^2+b^2+c^2+d^2=1 ,對應了三維球面\mathbb{S}^{3} .
由於任意兩個單位長度的四元數的乘積仍然是單位長度,所以\mathbb{S}^{3} 對乘法是封閉的。(實際上,\mathbb{S}^{3} 在四元數乘法下是一個群。)
四、等距同構
我們現在回過頭再看復數與旋轉的關系:
對於單位長度的復數u 來說,我們壓根不需要計算三角函數就可以知道它對應了旋轉。對於任意v,w 兩個復數,我們考慮它們的距離在乘u 前後的變化:
|uv-uw|=|u(v-w)|=|u||v-w|=|v-w|
可以看出,它們的距離沒有發生變化。用一個看起來高大上的術語來說,『乘u 』是一個『等距同構』。
同樣地,我們我們可以用這種方法證明:乘上一個單位長度的四元數也是\mathbb{R}^4 中的等距同構。
五、虛四元數的乘積
四元數對應了四維空間,而我們要研究的是三維空間的旋轉,所以我們把目光限定在四元數的一個子空間:『虛四元數』。
虛四元數就是實部為零的四元數,也就是形如p=b\mathrm{i}+c\mathrm{j}+d\mathrm{k} 的四元數。虛四元數構成了三維的空間,我們把它記作\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} .
顯然,\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中任意兩個元素的和還是在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中;然而當我們做乘法的時候,問題就出現了:
如果u=u_1\mathrm{i}+u_2\mathrm{j}+u_3\mathrm{k},~v=v_1\mathrm{i}+v_2\mathrm{j}+v_3\mathrm{k} ,那麽它們的乘積是:
uv=-(u_1v_1+u_2v_2+u_3v_3)
~~~~+(u_2v_3-u_3v_2)\mathrm{i}-(u_1v_3-u_3v_1)\mathrm{j}+(u_1v_2-u_2v_1)\mathrm{k}
或者寫成
uv=-u\cdot v+u\times v
由於u\cdot v 是實數,所以只有當u 與v 垂直時,uv 才在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中。
同時,註意到如果u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的單位向量,那麽u^2=-u\cdot u=-|u|^2=-1 .
六、四元數的共軛作用
現在我們試著用四元數表示三維空間\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的旋轉。
與復數一樣,對於一個單位長度的四元數t ,我們也可以把它寫成實部與虛部的和:
t=\cos\theta+u\sin\theta , 其中u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的單位向量。
我們希望把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 作為我們旋轉的空間,然而我們之前已經發現,對於q\in \mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 來說,qt 可能不在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之中。這怎麽辦呢?
答案是:共軛——t^{-1}qt 一定在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之中。
為什麽呢?首先我們註意到t^{-1}=\bar{t}/|t|^2=\cos\theta-u\sin\theta ,所以t^{-1} 存在。於是,在\mathbb{H} 中,乘t 與乘t^{-1} 都是\mathbb{H} 上的對射(因為可逆),所以q\rightarrow t^{-1}qt (稱為t 的共軛作用)也是\mathbb{H} 上的對射。
由於對於任意實(四元)數r 都有t^{-1}rt=r ,即t 的共軛作用把\mathbb{R} 映到其自身,於是也會把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 映到自身。也就是說,t 的共軛作用是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 上的對射,這就解決了之前『qt 乘積會跑到\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 之外』的問題。
好的,接下來我們可以具體來考察t 的共軛作用在三維空間\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的效果了。
七、共軛作用的效果
我們想要證明的是,給定t=\cos\theta+u\sin\theta ,其中u 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中的單位向量,那麽t 的共軛作用將把\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 繞著u 所在的軸\mathbb{R}u 旋轉2\theta .
證明分兩步,首先我們證明\mathbb{R}u 是旋轉軸。這也就意味著,我們要證明u 的所有實數倍的向量在t 的共軛作用下保持原位:
t^{-1}ut=(\cos\theta-u\sin\theta)u(\cos\theta+u\sin\theta)
=(u\cos\theta-u^2\sin\theta)(\cos\theta+u\sin\theta)
=(u\cos\theta+\sin\theta)(\cos\theta+u\sin\theta) (因為u^2=-1 )
=u(\cos^2\theta+\sin^2\theta)+\sin\theta\cos\theta+u^2\sin\theta\cos\theta
=u (因為u^2=-1 )
接下來,我們在\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 中選取垂直於u 的單位向量v ,令w=u\times v . 於是,\left\{ u,v,w \right\} 是\mathbb{R}\mathrm{i}+\mathbb{R}\mathrm{j}+\mathbb{R}\mathrm{k} 的一組規範正交基。
為了證明確實旋轉了2\theta ,我們只需要證明t^{-1}vt=v\cos2\theta-w\sin2\theta 以及t^{-1}wt=v\sin2\theta+w\cos2\theta 就好了。兩者證明類似,這裏只證明前者:
t^{-1}vt=(\cos\theta-u\sin\theta)v(\cos\theta+u\sin\theta)
=(v\cos\theta-uv\sin\theta)(\cos\theta+u\sin\theta)
=v\cos^2\theta-uv\sin\theta\cos\theta+vu\sin\theta\cos\theta-uvu\sin^2\theta
=v\cos^2\theta-2uv\sin\theta\cos\theta+u^2v\sin^2\theta (因為vu=-uv )
=v(\cos^2\theta-\sin^2\theta)-2w\sin\theta\cos\theta (因為u^2=-1,~uv=w )
=v\cos2\theta-w\sin2\theta
證明完畢!
於是,對於\mathbb{R}^3 中每一個旋轉,給定旋轉軸u 以及旋轉角\alpha ,都有一個單位長度的四元數t=\cos(\alpha/2)+u\sin(\alpha/2) 的共軛作用與之對應。
此外,註意到兩個旋轉的疊加仍然是一個旋轉,因為t_{2}^{-1}(t_{1}^{-1}qt_1)t_2=(t_{2}^{-1}t_{1}^{-1})q(t_1t_2)=t^{-1}qt ;以及,旋轉的逆也是一個旋轉。
同時,由於(-t)^{-1}s(-t)=t^{-1}st ,於是-t 對應了同一個旋轉,所以這是一個『二對一』的對應關系,也就是其他答主所說的『從Spin群到SO群的二重覆蓋對映』。
那麽就這樣=w=
參考資料:

(譯為【天真的謊言理論】或【樸素李理論】)











